Вероятность столкновения SHA1
Учитывая набор из 100 различных строк одинаковой длины, как вы можете количественно определить вероятность того, что коллизия SHA1 для строк вряд ли...?
3 ответа
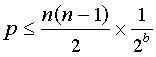
Достаточно ли велики 160-битные значения хеша, сгенерированные SHA-1, чтобы обеспечить уникальность отпечатка каждого блока? Предполагая случайные значения хеш-функции с равномерным распределением, набор из n различных блоков данных и хеш-функцию, которая генерирует b битов, вероятность p того, что произойдет одно или несколько коллизий, ограничена количеством пар блоков, умноженным на вероятность того, что данная пара столкнется.
(источник: http://web.archive.org/web/20110725085124/http://bitcache.org/faq/hash-collision-probabilities)
Ну, вероятность столкновения будет:
1 - ((2^160 - 1) / 2^160) * ((2^160 - 2) / 2^160) * ... * ((2^160 - 99) / 2^160)
Подумайте о вероятности столкновения 2 предметов в промежутке 10. Первый предмет уникален с вероятностью 100%. Второе уникально с вероятностью 9/10. Таким образом, вероятность того, что оба уникальны 100% * 90%и вероятность столкновения равна:
1 - (100% * 90%), or 1 - ((10 - 0) / 10) * ((10 - 1) / 10), or 1 - ((10 - 1) / 10)
Это довольно маловероятно. У вас должно быть много строк для удаленной возможности.
Посмотрите на таблицу на этой странице в Википедии; просто интерполируйте между строками 128 бит и 256 бит.
Это проблема дня рождения - статья содержит хорошие аппроксимации, которые позволяют довольно легко оценить вероятность. Фактическая вероятность будет очень очень очень низкой - см. Этот вопрос для примера.