Полярная диаграмма Эффект Магнуса не показывает правильные данные
Я хотел построить уравнения скорости обтекания вращающегося цилиндра на полярной диаграмме. (Уравнения взяты из "Основ аэродинамики" Андерсена.) Вы можете увидеть два уравнения внутри операторов цикла.
Я не могу из-за громкого крика представить расчетные данные на полярный график. Я испробовал каждую свою идею, но никуда не попал. Я проверил данные, и этот, кажется, все правильно, так как он ведет себя так, как должен.
Вот код моей последней попытки:
import numpy as np
import matplotlib.pyplot as plt
RadiusColumn = 1.0
VelocityInfinity = 10.0
RPM_Columns = 0.0#
ColumnOmega = (2*np.pi*RPM_Columns)/(60)#rad/s
VortexStrength = 2*np.pi*RadiusColumn**2 * ColumnOmega#rad m^2/s
NumberRadii = 6
NumberThetas = 19
theta = np.linspace(0,2*np.pi,NumberThetas)
radius = np.linspace(RadiusColumn, 10 * RadiusColumn, NumberRadii)
f = plt.figure()
ax = f.add_subplot(111, polar=True)
for r in xrange(len(radius)):
for t in xrange(len(theta)):
VelocityRadius = (1.0 - (RadiusColumn**2/radius[r]**2)) * VelocityInfinity * np.cos(theta[t])
VelocityTheta = - (1.0 + (RadiusColumn**2/radius[r]**2))* VelocityInfinity * np.sin(theta[t]) - (VortexStrength/(2*np.pi*radius[r]))
TotalVelocity = np.linalg.norm((VelocityRadius, VelocityTheta))
ax.quiver(theta[t], radius[r], theta[t] + VelocityTheta/TotalVelocity, radius[r] + VelocityRadius/TotalVelocity)
plt.show()
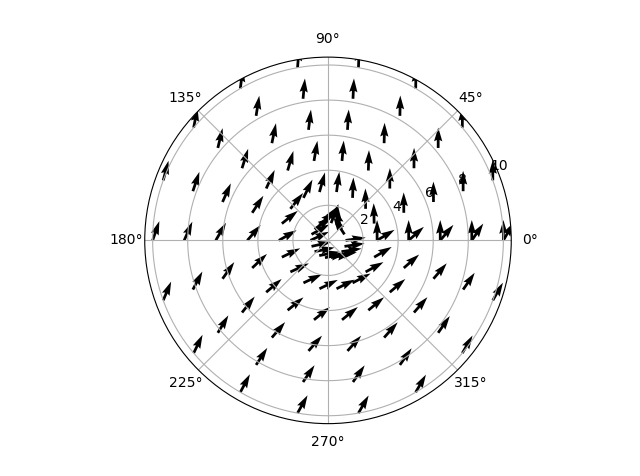
Как вы можете видеть, я установил обороты на 0. Это означает, что поток должен идти слева направо и быть симметричным по горизонтальной оси. (Поток должен проходить вокруг цилиндра одинаково с обеих сторон.) Результат, однако, выглядит примерно так:
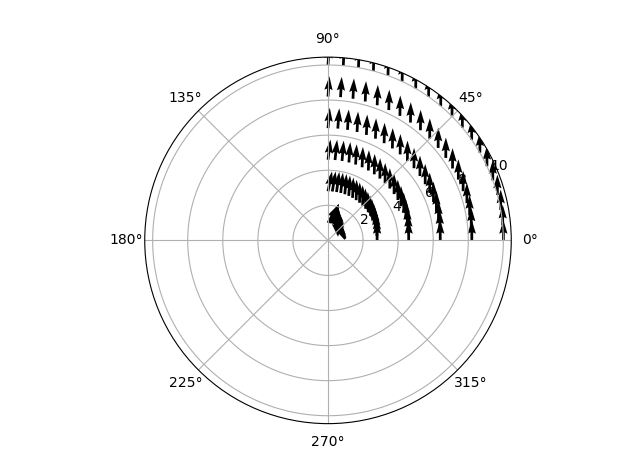
Это полная чушь. Кажется, что есть завихренность, даже когда ничего не установлено! Еще более странно, когда я отображаю только данные от 0 до pi/2, поток меняется!
Как видно из кода, я пытался использовать единичные векторы, но, очевидно, это не тот путь. Буду признателен за любой полезный вклад.
Спасибо!
1 ответ
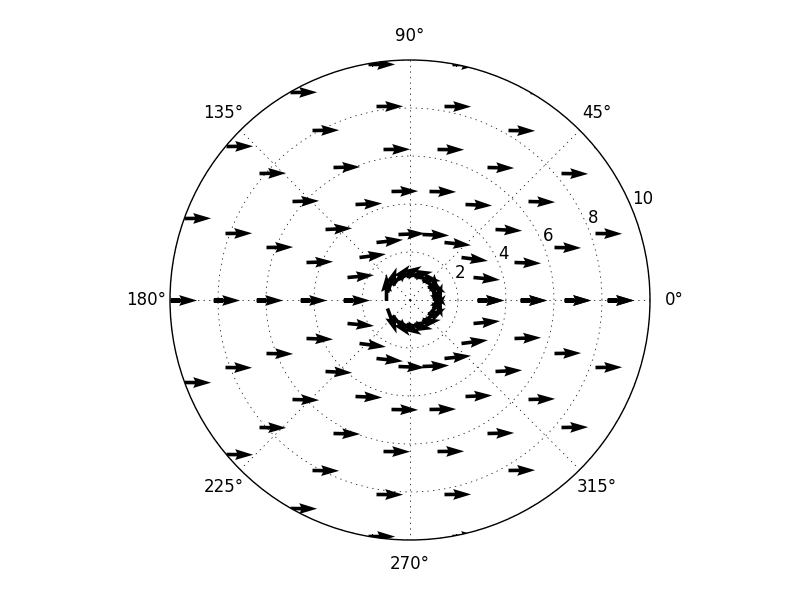
Основная проблема заключается в том, что .quiver метод полярного Axes объект по-прежнему ожидает, что его компоненты вектора в декартовых координатах, поэтому вам нужно преобразовать свои тэта и радиальные компоненты в x и y самостоятельно:
for r in xrange(len(radius)):
for t in xrange(len(theta)):
VelocityRadius = (1.0 - (RadiusColumn**2/radius[r]**2)) * VelocityInfinity * np.cos(theta[t])
VelocityTheta = - (1.0 + (RadiusColumn**2/radius[r]**2))* VelocityInfinity * np.sin(theta[t]) - (VortexStrength/(2*np.pi*radius[r]))
TotalVelocity = np.linalg.norm((VelocityRadius, VelocityTheta))
ax.quiver(theta[t], radius[r],
VelocityRadius/TotalVelocity*np.cos(theta[t])
- VelocityTheta/TotalVelocity*np.sin(theta[t]),
VelocityRadius/TotalVelocity*np.sin(theta[t])
+ VelocityTheta/TotalVelocity*np.cos(theta[t]))
plt.show()
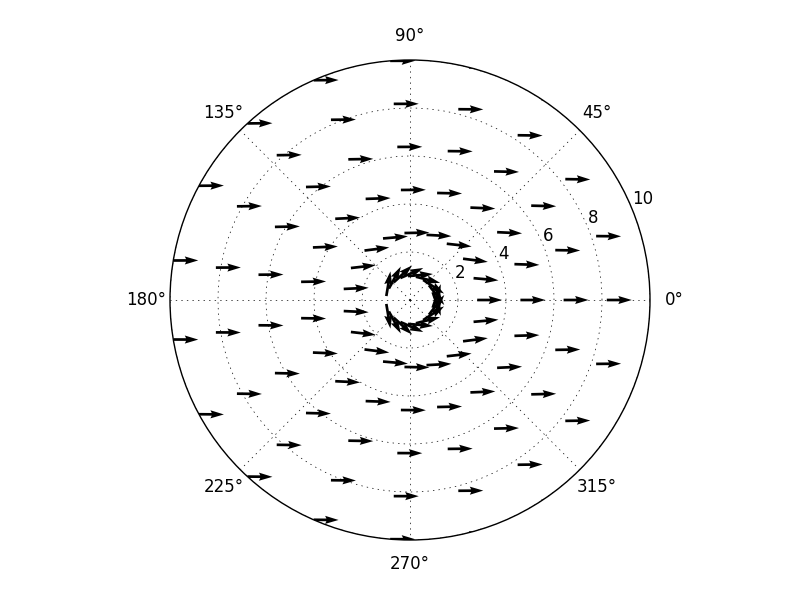
Тем не менее, вы можете значительно улучшить свой код, используя векторизацию: вам не нужно перебирать каждую точку, чтобы получить то, что вам нужно. Так что эквивалент вашего кода, но еще понятнее:
def pol2cart(th,v_th,v_r):
'''convert polar velocity components to Cartesian, return v_x,v_y'''
return v_r*np.cos(th) - v_th*np.sin(th), v_r*np.sin(th) + v_th*np.cos(th)
theta = np.linspace(0,2*np.pi,NumberThetas,endpoint=False)
radius = np.linspace(RadiusColumn, 10 * RadiusColumn, NumberRadii)[:,None]
f = plt.figure()
ax = f.add_subplot(111, polar=True)
VelocityRadius = (1.0 - (RadiusColumn**2/radius**2)) * VelocityInfinity * np.cos(theta)
VelocityTheta = - (1.0 + (RadiusColumn**2/radius**2))* VelocityInfinity * np.sin(theta) - (VortexStrength/(2*np.pi*radius))
TotalVelocity = np.linalg.norm([VelocityRadius, VelocityTheta],axis=0)
VelocityX,VelocityY = pol2cart(theta,VelocityTheta,VelocityRadius)
ax.quiver(theta,radius, VelocityX/TotalVelocity, VelocityY/TotalVelocity)
plt.show()
Несколько заметных изменений:
- я добавил
endpoint=Falseвtheta: так как ваша функция периодическая в2*piВам не нужно наносить конечные точки дважды. Обратите внимание, что это означает, что в настоящее время у вас есть больше видимых стрелок; если вы хотите оригинальное поведение, я предлагаю вам уменьшитьNumberThetasодним. - я добавил
[:,None]вradius: это сделает его двумерным массивом, поэтому дальнейшие операции по определению скоростей приведут к двухмерным массивам: разные столбцы соответствуют разным углам, разные строки соответствуют разным радиусам.quiverсовместим с входным значением массива, поэтому один вызовquiverбудет делать вашу работу. - Поскольку скорости теперь являются 2d массивами, нам нужно вызвать
np.linalg.normпо существу, в трехмерном массиве, но это работает, как и ожидалось, если мы указываем ось для работы над. - Я определил
pol2cartвспомогательная функция для преобразования из полярных в декартовы компоненты; в этом нет необходимости, но мне кажется, это понятнее.
Последнее замечание: я предлагаю выбирать более короткие имена переменных и те, которые не имеют CamelCase. Это, вероятно, ускорит ваше кодирование.