Stepinfo в Python
Я пытаюсь определить следующие характеристики шага для ответа шага в Python:
- Время нарастания
- SettlingTime
- SettlingMin
- SettlingMax
- выброс
- недолет
- Пик
- Час пик
Matlab предлагает мне функцию stepinfo, но я не могу найти подходящую альтернативу в Python. Я пытался накатить свои собственные, используя numpy и scipy, но мне пока не очень повезло, мои знания по обработке сигналов отсутствуют.
Большая часть информации, которую я могу найти в Интернете, выглядит довольно сложной, но мне нравится больше узнавать об этом. Если бы кто-нибудь мог порекомендовать мне хорошую книгу или другой источник, чтобы узнать больше, я был бы признателен за это! Спасибо!
Это ответ на шаг, который у меня сейчас есть:
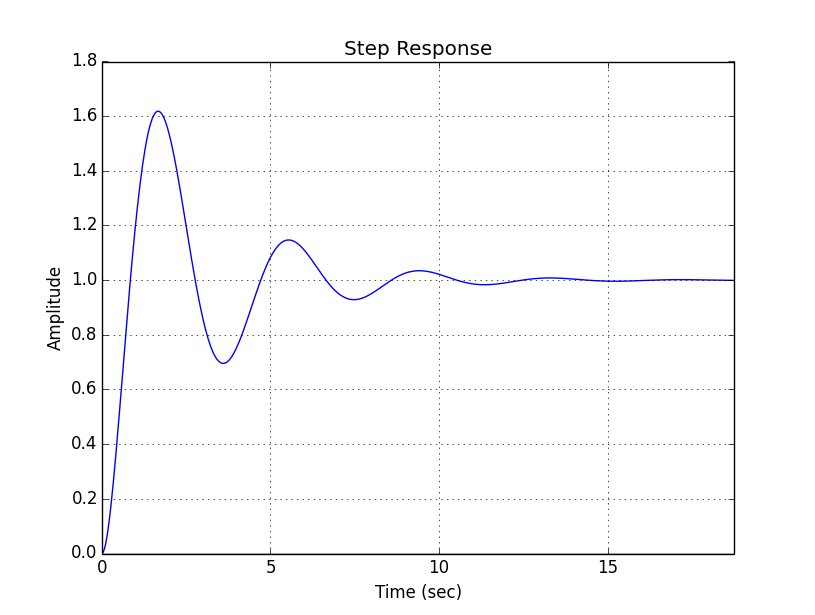
2 ответа
Это обсуждение предлагает своего рода реализацию:
def step_info(t,yout):
print "OS: %f%s"%((yout.max()/yout[-1]-1)*100,'%')
print "Tr: %fs"%(t[next(i for i in range(0,len(yout)-1) if yout[i]>yout[-1]*.90)]-t[0])
print "Ts: %fs"%(t[next(len(yout)-i for i in range(2,len(yout)-1) if abs(yout[-i]/yout[-1])>1.02)]-t[0])
Затем вам нужно использовать функции numpy в разделе "Обработка сигналов", чтобы получить другую необходимую вам информацию.
Не могли бы вы просто реализовать формулы? (Предполагая, что это система второго порядка / имеет два доминирующих полюса и может быть аппроксимирована как второй порядок)
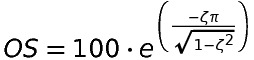
Для времени нарастания и посадки есть несколько разных приближений, поэтому интернет - ваш друг.
Вы также можете вычислить демпфированную частоту (из максимумов и минимумов данных вашего графика) и использовать ее для определения собственной частоты:
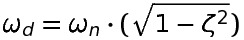
Есть несколько формул, которые связывают эти различные величины, в зависимости от того, что вы знаете.