Почему число поддеревьев, полученных в результате запроса дерева диапазонов, равно O(log(n))?

Question

Я пытаюсь выяснить эту структуру данных, но я не понимаю, как мы можем сказать, что есть O(log(n)) поддеревьев, которые представляют ответ на запрос?

Вот картинка для иллюстрации:

Спасибо!

Answer 1

Если мы сделаем предположение, что приведенное выше является чисто функциональным двоичным деревом [wiki], поэтому, когда узлы неизменны, мы можем сделать "копию" этого дерева таким образом, чтобы только элементы имели значение больше, чем x_1, и меньше, чем х₂ в дереве.

Давайте начнем с очень простого случая, чтобы проиллюстрировать это. Представьте, что у нас просто нет никаких границ, чем мы можем просто вернуть все дерево. Таким образом, вместо создания нового дерева, мы возвращаем ссылку на корень дерева. Таким образом, мы можем без каких-либо границ вернуть дерево в O (1), учитывая, что дерево не редактируется (по крайней мере, пока мы используем поддерево).

Вышеприведенный случай, конечно, довольно прост. Мы просто делаем "копию" (на самом деле не копию, поскольку данные неизменны, мы можем просто вернуть дерево) всего дерева. Итак, давайте стремимся решить более сложную проблему: мы хотим построить дерево, которое содержит все элементы, превышающие пороговое значение x₁. Для этого мы можем определить рекурсивный алгоритм:

1. урезанная версия None (или что-либо представляет пустую ссылку, или ссылку на пустое дерево) None;
2. если значение узла меньше порогового значения, мы возвращаем "вырезанную" версию правого поддерева; а также
3. если узел имеет значение, превышающее пороговое значение, мы возвращаем индекс, который имеет такое же правое поддерево, а в качестве левого подшилька - вырезанную версию левого подшильда.

Так что в псевдокоде это выглядит так:

def treelarger(some_node, min):
    if some_tree is None:
        return None
    if some_node.value > min:
        return Node(treelarger(some_node.left, min), some_node.value, some_node.right)
    else:
        return treelarger(some_node.right, min)

Таким образом, этот алгоритм выполняется в O(h) с h высотой дерева, так как для каждого случая (кроме первого) мы рекурсируем одному (не обоим) дочерним элементам, и он заканчивается, если у нас есть узел без children (или, по крайней мере, не имеет поддерева в направлении, в котором нам нужно вырезать поддерево).

Таким образом, мы не делаем полную копию дерева. Мы повторно используем много узлов в старом дереве. Мы только создаем новую "поверхность", но большая часть "объема" является частью старого двоичного дерева. Хотя само дерево содержит O(n) узлов, мы создаем, самое большее, O(h) новых узлов. Мы можем оптимизировать вышеперечисленное так, чтобы, учитывая, что урезанная версия одного из поддеревьев одинакова, мы не создаем новый узел. Но это даже не имеет большого значения с точки зрения сложности времени: мы генерируем не более O(h) новых узлов, и общее число узлов либо меньше, чем исходное число, либо совпадает.

В случае полного дерева высота дерева h масштабируется с O(log n), и, таким образом, этот алгоритм будет работать в O(log n).

Тогда как мы можем сгенерировать дерево с элементами между двумя порогами? Мы можем легко переписать вышесказанное в алгоритм treesmaller который генерирует поддерево, которое содержит все элементы меньшего размера:

def treesmaller(some_node, max):
    if some_tree is None:
        return None
    if some_node.value < min:
        return Node(some_node.left, some_node.value, treesmaller(some_node.right, max))
    else:
        return treesmaller(some_node.left, max)

грубо говоря, есть два различия:

1. мы меняем условие с some_node.value > min в some_node.value < max; а также
2. мы возвращаемся на right subchild, если условие выполнено, и слева, если оно не выполняется.

Теперь выводы, которые мы делаем из предыдущего алгоритма, также являются выводами, которые могут быть применены к этому алгоритму, поскольку он снова вводит только O(h) новых узлов, а общее количество узлов может только уменьшаться.

Хотя мы можем построить алгоритм, который одновременно учитывает два порога, мы можем просто повторно использовать вышеупомянутые алгоритмы для создания поддерева, содержащего только элементы в пределах диапазона: сначала мы передаем дерево treelarger функция, а затем этот результат через treesmaller (или наоборот).

Поскольку в обоих алгоритмах мы вводим O(h) новых узлов, а высота дерева не может увеличиваться, мы, таким образом, строим не более O(2 h) и, следовательно, O(h) новых узлов.

Если исходное дерево было полным деревом, то оно, таким образом, считает, что мы создаем O(log n) новых узлов.

Answer 2

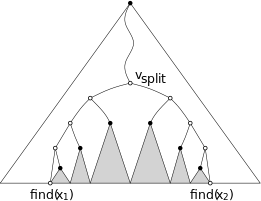
Рассмотрим поиск двух конечных точек диапазона. Этот поиск будет продолжаться до тех пор, пока не будет найден наименьший общий предок двух листовых узлов, охватывающих ваш интервал. В этот момент поиск разветвляется: одна часть перемещается влево, а другая - вправо. А пока давайте сосредоточимся на той части запроса, которая разветвляется влево, поскольку логика такая же, но обратная для правой ветви.

В этом поиске полезно думать о каждом узле не как о единственной точке, а как о диапазоне точек. Таким образом, общая процедура такова:

1. Если диапазон запроса полностью включает диапазон, представленный этим узлом, прекратите поиск по x и начните поиск в поддереве y этого узла.

2. Если диапазон запроса находится исключительно в диапазоне, представленном правым поддеревом этого узла, продолжайте поиск x вправо и не исследуйте поддерево y.

3. Если диапазон запроса перекрывает диапазон левого поддерева, тогда он должен полностью включать диапазон правого поддерева. Итак, обработайте y-поддерево правого поддерева, а затем рекурсивно исследуйте x-поддерево слева.

Во всех случаях мы добавляем не более одного y-поддерева для рассмотрения, а затем рекурсивно продолжаем исследование x-поддерева только в одном направлении. Это означает, что мы, по сути, прослеживаем путь вниз по x-дереву, добавляя не более одного y-поддерева за шаг. Поскольку дерево имеет высоту O(log n), общее количество y-поддеревьев, посещенных таким образом, равно O(log n). А затем, включая количество посещенных y-поддеревьев в случае, когда мы разветвлялись прямо наверху, мы получаем еще O(log n) поддеревьев для поиска в общей сложности O(log n) поддеревьев.

Надеюсь это поможет!