Алгоритм поиска дизъюнктного объединения на графе зависимостей

Question

Прежде всего, некоторый контекст о проблеме:

Я работаю в системе, которая имеет несколько типов ресурсов (A, B, C...). Мне даны некоторые требования к ресурсам, и я должен определить, могу ли я их себе позволить.

Для этого у меня есть несколько источников, каждый из которых может предоставить более одного типа ресурса, но мне нужно выбрать, какой из них я использую для каждого ресурса.

Например, если мне нужно заплатить 1A, 2B и 0C (представлены как (1,2,0)), и у меня есть следующие источники:

1. (1,1,0) // Значит я должен выбрать продукцию А или Б
2. (0,1,1) // Значит, я должен выбрать продукцию B или C
3. (1,1,0)

Очевидно, что я должен использовать источник 2 для ресурса B, и я могу выбрать для 1 и 3, какой из них производит A и B

Мой подход для реализации этого состоит в том, чтобы рассматривать его как график зависимости, где описанная выше ситуация представлена ​​следующим образом:

Таким образом, я зацикливаюсь на ресурсах, и для каждого ресурса я зацикливаюсь на ссылках, достигающих его. Если удаление текущего узла для текущего ресурса означает, что у других ресурсов осталось оставшихся достигающих ссылок для оплаты оставшейся стоимости, я использую его.

В предыдущем примере я сначала пытаюсь использовать источник 1 для ресурса A. В B все еще есть 2 ссылки, поэтому я могу это сделать. Для оплаты оставлены только ресурсы типа B, поэтому я использую оставшиеся источники для оплаты B.

Все в порядке, но теперь мне нужно работать в новом сценарии, где есть два типа источников, каждый из которых производит один тип ресурса по стоимости 1 или 2, и мне нужно минимизировать общую стоимость.

Небольшое изменение в примере может быть таким:

Решение здравого смысла должно состоять в том, чтобы использовать 1 и 2 для оплаты B, и использовать 3 для оплаты A за общую стоимость 1, но в моей реализации, как описано выше, источник 1 используется для оплаты A, поскольку B все еще имеет 2 ссылки на это, так что в конце я должен использовать источник 3 со стоимостью 2.

По возможности следует избегать решений, предполагающих использование всех комбинаций выбора.

Знаете ли вы о какой-либо общей алгоритмической проблеме с известным решением, которая может быть применена к этому случаю? Или как улучшить мое реальное решение для работы в этом новом сценарии? Или я должен выбрать другой подход?

Answer 1

Эта проблема сводится к поиску максимального потока в сети потоков.

Вот идея:

1. Для каждого типа ресурса (A, B, ...) узел с входящим ребром от исходного узла (исходный узел не имеет ничего общего с источниками из проблемы, это общая метка, используемая в теории сетевого потока, обычно отмечен s) с мощностью, равной требуемому количеству данного ресурса. Например, если вам нужно 2B, емкость будет 2.

2. Для каждого источника (под этим я подразумеваю источник, как определено описанием проблемы), вы создаете узел с исходящим ребром в приемник (обычно отмеченный t) с емкостью 1.

3. От каждого узла с шага 1. добавьте исходящий фронт к каждому из узлов с шага 2., которые обеспечивают, что может обеспечить требуемый тип ресурса.

Например, график для вашей ситуации будет выглядеть так:

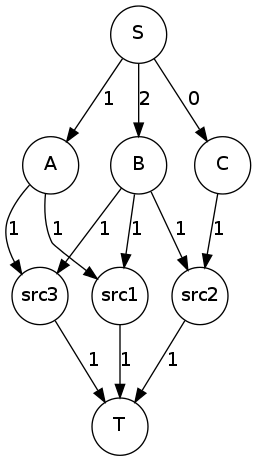
Теперь максимальный поток ST в этой сети даст вам ответ. В основном насыщенные ребра между узлами типов (A, B, C) и узлами- источниками (src1, src2, src3) скажут вам, какой источник должен предоставлять какой тип ресурса.

Максимальный поток может быть найден с использованием любого из классических алгоритмов, таких как увеличение пути(Форд-Фулкерсон, Диник и т. Д.) Или один из методов толкания-перемычки (Гольдберг-Тарьян, Релабел-на-Фронт и т. Д.).

Это конкретное применение максимального потока также можно рассматривать как своего рода обобщенное двустороннее сопоставление, когда вы сопоставляете каждый тип ресурса, возможно, с несколькими источниками, но каждый источник может обрабатывать только один ресурс. Идея легко распространяется на случай, когда источник может обрабатывать более одного типа (путем простого изменения емкости src-T edge от 1 до желаемых).