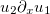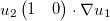Производные термины в фипах

Question

Каков правильный подход к терминам, содержащим производные, которые нельзя представить (по крайней мере, каким-либо очевидным образом) как конвекцию или диффузию в FiPy? Например, в системе уравнений в частных производных, которые решаются для функций u_i в 2-й области с координатами x, y, одно из уравнений содержит член

u_2 * \partal_x u_1

Я могу представить его как источник, учитывая, что x и u_i являются переменными ячейки:

eq = ... + fipy.tools.numerix.dot(x.grad,u_1.grad) * u_2

Однако из-за того, как градиент вычисляется в FiPy, x.grad является вектором со значением (1,0) везде, кроме ячеек, расположенных непосредственно рядом с границей x, где он становится (2,0). Это означает, что я должен использовать вектор (1,0) вместо x.grad с самого начала. Но в этот момент я не уверен, будет ли у u_1.grad правильное значение на границах для представления моего термина, и, скорее всего, весь мой подход неверен. Что я должен сделать, чтобы представить такой термин?

Answer 1

[отредактированный ответ, чтобы отразить заданный вопрос]

эквивалентно , который отображается в FiPy как:

eq = ... + fp.ImplicitSourceTerm(coeff=fp.tools.numerix.dot([[1], [0]], u1.grad), var=u2)