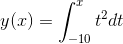Как интегрировать правило Симпсонов с помощью Scipy для построения одномерного графика

Question

Мне нужна помощь, у меня есть задание на код интеграции функции с использованием правила Симпсонов. Мне нужно использовать встроенную функцию scipy integratesimps для построения одномерного графика. Я просто не знаю с чего начать. Я думаю, что я должен получить список / массив каждого значения y для функции, которая соответствует каждому значению x: например

если моя функция равна x^2, то когда x равен 0, y равен 0, x равен 1, y равен 1, x равен 2, y равен 4, и так далее до огромного предела...

и затем используйте integrate.simps(y,x), где y - все значения y, как показано выше, а x - все соответствующие значения x.

Тем не менее, я не могу заставить его работать вообще... у кого-нибудь есть примеры графика для функции x^2 с использованием integrate.simps(y,x)?

вот что у меня так далеко:

import numpy as np
from scipy import integrate
import matplotlib.pyplot as plt

x = np.linspace(-10,10,N)
N = 100

yarray = []

def f(x):
    return x**2

for i in x :
    y = f(i)
    yarray.append(y)

print(yarray)


E = integrate.simps(yarray,x)
print(E)

plt.plot(x,E)

Answer 1

По сути, вам нужно вычислить интегральное значение для каждого диапазона x, от [-10,-10] до [-10,10]

Этот пример кода участков

import numpy as np
from scipy import integrate
import matplotlib.pyplot as plt

def f(x):
    return x**2

N = 100
x = np.linspace(-10,10,N)


integrals = []
x_range = []
y_range = []
for i in x:
    x_range.append(i)
    y_range.append(f(i))
    integral = integrate.simps(y_range, x_range)
    integrals.append(integral)

plt.plot(x, integrals)
plt.show()

Завернуть это

import numpy as np
from scipy import integrate
import matplotlib.pyplot as plt

def integrals(f, xs):
    x_range = []
    y_range = []
    results = []
    for x in xs:
        x_range.append(x)
        y_range.append(f(x))
        integral = integrate.simps(y_range, x_range)
        results.append(integral)
    return results

def f(x, b):
    return (x-b)**2

xs = np.linspace(-10, 10, 100)

plt.plot(xs, integrals(lambda x: f(x, 0), xs), label='b=0')
plt.plot(xs, integrals(lambda x: f(x, 2), xs), label='b=2')
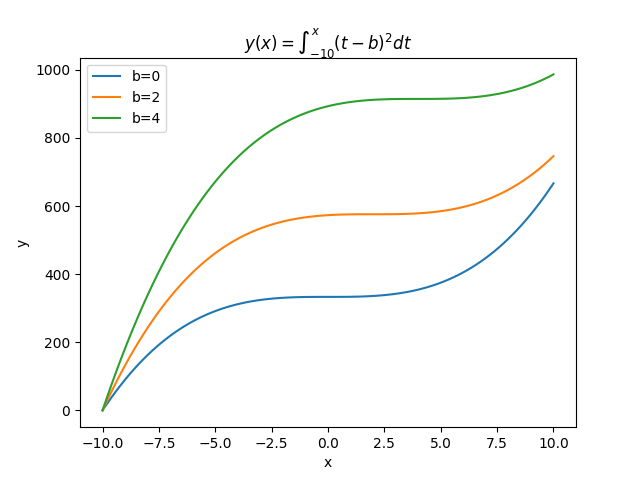
plt.plot(xs, integrals(lambda x: f(x, 4), xs), label='b=4')
plt.title('$y(x) = \int_{-10}^{x}(t-b)^2dt$')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()

и вы получите