Maple: Как преобразовать цилиндрические координаты в декартовы?

Question

Мы получаем некоторое выражение в цилиндрических координатах (r, ϕ, z), например: expr := r*z^2*sin((1/3)*φ) нам нужно преобразовать его в декартовы координаты, а затем обратно в цилиндрические координаты. Как это сделать?

Итак, я нашел что-то вроде этого: eval(expr, {r = sqrt(x^2+y^2), z = z,φ= arctan(y, x)}) но кажется неправильным, как это исправить и как сделать eval для преобразования обратных слов из декартовой в цилиндрическую?

ϕ == ϕ

Итак, я стараюсь:

R := 1; 

H := h; 

sigma[0] := sig0;

sigma := sigma[0]*z^2*sin((1/3)*`ϕ`);

toCar := eval(sigma, {r = sqrt(x^2+y^2), z = z, `ϕ` = arctan(y, x)});

toCyl := collect(eval(toCar, {x = r*cos(`ϕ`), y = r*sin(`ϕ`), z = z}), `ϕ`)

Это выглядит близко к истине, но посмотрите: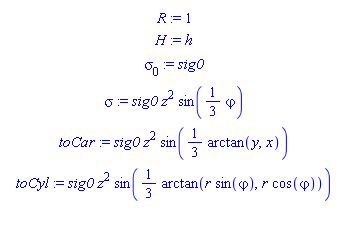

Зачем arctan(r*sin(φ), r*cos(φ)) не отображается как ϕ?

На самом деле это только начало веселья для меня, потому что мне также нужно рассчитать

Q := int(int(int(toCar, x = 0 .. r), y = 0 .. 2*Pi), z = 0 .. H)

и вернуть его в цилиндрические координаты...

Answer 1

simplify(toCyl) assuming r>=0, `&varphi;`<=Pi, `&varphi;`>-Pi;

Обратите внимание,

arctan(sin(Pi/4),cos(Pi/4));
                          1   
                          - Pi
                          4   

arctan(sin(Pi/4 + 10*Pi),cos(Pi/4 + 10*Pi));
                          1   
                          - Pi
                          4   

arctan(sin(-7*Pi/4),cos(-7*Pi/4));
                          1   
                          - Pi
                          4   

arctan(sin(-15*Pi/4),cos(-15*Pi/4));
                          1   
                          - Pi
                          4   


arctan(sin(-Pi),cos(-Pi));
                           Pi

K:=arctan(r*sin(Pi/4),r*cos(Pi/4));
                      arctan(r, r)

simplify(K) assuming r<0;
                           3   
                         - - Pi
                           4   

simplify(K) assuming r>0;
                          1   
                          - Pi
                          4   

Как только вы преобразуете из цилиндрического в прямоугольное, любая информация о том, сколько раз исходный угол "мог обернуться вокруг (прошлое -Pi), будет потеряна.

Таким образом, вы не будете восстанавливать оригинал ϕ если это не было в (-Pi,Pi]. Если вы скажете Maple, что это так (вместе с r>-0, чтобы он знал, в какой полуплоскости), используя предположения, то это может упростить до того, что вы ожидаете.