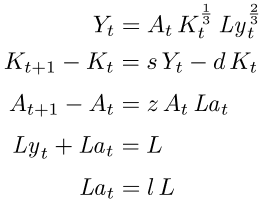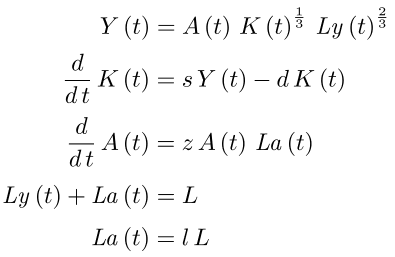Численное решение систем разностных / дифференциальных алгебраических уравнений в максимумах
Я начну с системы разностных уравнений (упрощенная экономическая модель Солоу-Ромер):
Где t нижние индексы указывают дискретное время, например Y[t=0], Y[t=1], Y[t=2], ...
В частности:
eq1: Y[t] = A[t]*K[t]^(1/3)*Ly[t]^(2/3);
eq2: K[t+1] - K[t] = s*Y[t] - d*K[t];
eq3: A[t+1] - A[t] = z*A[t]*La[t];
eq4: Ly[t] + La[t] = L;
eq5: La[t] = l*L;
Endogenous variables (unknowns), and their initial conditions:
Y[t] Y[0] = 9663.8253
K[t] K[0] = 100.0
A[t] A[0] = 100.0
Ly[t] Ly[0] = 95.0
La[t] La[0] = 5.0
Exogenous variables (givens):
s: 0.15;
d: 0.07;
z: 0.02;
l: 0.05;
L: 100.0;
Это 5 уравнений в 5 неизвестных. Численное решение системы на практике тривиально: вы просто начинаете с t=0 с начальными условиями, рассчитать K[1] а также A[1] из разностных уравнений, а затем рассчитать Y[1] От этого.
Несмотря на его тривиальный характер, я не смог определить, как на самом деле это сделать, и построить результирующие кривые в Maxima.
Я вполне доволен подходом дифференциальных уравнений (действительно дифференциально-алгебраическим), если это более благоприятно для возможностей Maxima. В любом случае это должно быть эквивалентно численному решению:
То есть:
eq1: Y(t)=A(t)*K(t)^(1/3)*Ly(t)^(2/3);
eq2: diff(K(t),t) = s*Y(t)-d*K(t);
eq3: diff(A(t),t) = z*A(t)*La(t);
eq4: Ly(t)+La(t) = L;
eq5: La(t) = l*L;
Но, опять же, я не вижу способа численного решения и построения этой системы с помощью Рунге-Кутты или других встроенных решателей (и это действительно так, хотя приведенные выше алгебраические уравнения можно легко переписать в виде 0=f(Y,A,K,Ly,La)).
На данный момент я не добился никакого прогресса. Единственный инструмент, который я вижу для разностных уравнений (diff_rec2) предназначен для символических решений таких систем, но в целом экономические модели не выражаются в замкнутой форме. Рунге-Кутта (rk) не принимает алгебраические уравнения (насколько я вижу), и я не уверен, где искать дальше.
В конечном счете, я думаю, что это было бы очень просто, учитывая прямую природу вычисления времени вперед этой и подобных моделей. Тем не менее, я хочу избежать ручных манипуляций или превращения этого в особый случай. Меня особенно интересует метод общего решения для систем таких уравнений, так как я планирую реализовать в будущем более сложные модели, такие как открытая экономика Маккиннона (1997).
Редактировать:
Благодаря (принятому) ответу Роберта, вот полностью работающее решение для копирования-вставки для приведенного выше примера уравнения разности времени вперед:
Y[t] := A[t]*K[t]^(1/3)*Ly[t]^(2/3);
K[t] := K[t - 1] + s*Y[t - 1] - d*K[t - 1];
A[t] := A[t - 1] + z*A[t - 1]*La[t - 1];
Ly[t] := L - La[t];
La[t] := l*L;
s : 0.15;
d : 0.07;
z : 0.02;
l : 0.05;
L : 100.0;
A[0] : 100.0;
K[0] : 100.0;
sol : makelist ([Y[n], K[n], A[n], Ly[n], La[t]], n, 0, 30);
v : makelist ([p-1, sol[p][1]], p, 1, 30);
plot2d ([discrete,v,0,30], logy);
1 ответ
Что ж, если цель состоит в том, чтобы вычислить решение для данных уравнений, я думаю, вы можете сделать это с помощью так называемых функций запоминания (то есть функций, которые вычисляют результат и запоминают его). В Maxima такие функции определяются f[k] := ... (вместо f(k) := ... для обычных, не запоминающих функций). В этом случае я думаю, что вы бы:
Y[t] := A[t]*K[t]^(1/3)*Ly[t]^(2/3);
K[t] := K[t - 1] + s*Y[t - 1] - d*K[t - 1];
A[t] := A[t - 1] + z*A[t - 1]*La[t - 1];
Ly[t] := L - La[t];
La[t] := l*L;
Y[0] : 9663.8253;
K[0] : 100;
A[0] : 100;
Ly[0] : 95.0;
La[0] : 5.0;
s: 0.15;
d: 0.07;
z: 0.02;
l: 0.05;
L: 100.0;
и тогда вы можете вычислить, например, makelist ([Y[n], K[n], A[n], Ly[n], La[t]], n, 1, 10);
Это работает, если вы можете изменить уравнения самостоятельно; в этом случае это просто. Если вам нужно решить другие проблемы, и такой подход не поможет, вам понадобится что-то более мощное. Я не знаю, что предложить. Мой совет - спросить в списке рассылки maxima-discuss@lists.sourceforge.net, где больше всего обсуждается Maxima.