Получение границы прямоугольника с использованием выпуклой оболочки (в питоне)

Question

Я пытаюсь получить границу прямоугольника, используя scipy.ConvexHull()и это не в состоянии сделать это.

u=np.linspace(0, 4, 8)
v=np.linspace(5, 10, 8)
u,v=np.meshgrid(u,v)
u=u.flatten()
v=v.flatten()
points2D=np.vstack([u,v]).T


hull = ConvexHull(points2D)
convex_hull_plot_2d(hull)
boundaryList = hull.vertices
print boundaryList

дает только четыре угла:[ 0 7 63 56]

Немного возмущаем точки, используя опцию qhull_options="QJ Pp" следующее:

 hull = ConvexHull(points2D, qhull_options="QJ Pp")

дает больше очков: [62 56 40 8 0 2 6 7 15 23 47 55 63], но все же не полный набор границ.

Может кто-нибудь сказать мне правильное решение для этого?

Answer 1

Математическое определение выпуклых состояний корпуса

В математике выпуклая оболочка или выпуклая оболочка множества X точек в евклидовой плоскости или в евклидовом пространстве (или, в более общем случае, в аффинном пространстве над реалами) является наименьшим выпуклым множеством, содержащим X.

Самый маленький выпуклый набор, содержащий прямоугольник, - это действительно четыре угла, которые вы получаете.

Чтобы получить все точки на границе, вы можете использовать триангуляцию Делоне, а затем вычислить выпуклую оболочку из полученной сетки Делоне,

import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial import Delaunay

u=np.linspace(0, 4, 8)
v=np.linspace(5, 10, 8)
u,v=np.meshgrid(u,v)
u=u.flatten()
v=v.flatten()
points2D=np.vstack([u,v]).T

tri = Delaunay(points2D)
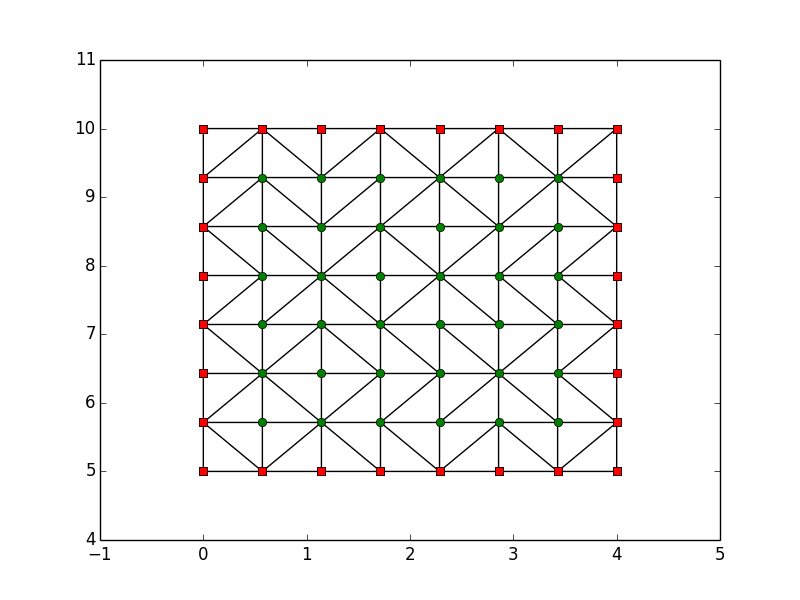
plt.triplot(points2D[:,0], points2D[:,1], tri.simplices.copy())

boundary = (points2D[tri.convex_hull]).flatten()
bx = boundary[0:-2:2]
by = boundary[1:-1:2]

plt.plot(points2D[:,0], points2D[:,1], 'o')
plt.plot(bx, by, 'rs')

plt.xlim(-1,5)
plt.ylim(4,11)
plt.show()

Для создания корпуса после формирования триангуляции программа использует tri.convex_hull. Это возвращает вершины граней, образующих выпуклую оболочку для точек триангуляции. В вашем двумерном случае это линии, и результат получается в виде набора соседних точек, составляющих каждую линию. Обратите внимание, что этот подход считается неэффективным, поскольку он должен формировать триангуляцию в дополнение к выпуклой оболочке.

Оставшаяся часть программы извлекает x и соответствующие значения y для каждой точки и строит их вместе с триангуляцией, что приводит к