Распознавание фигур с помощью numpy/scipy (возможно, водораздел)

Question

Моя цель - отследить рисунки, в которых много разных фигур, и разбить их на отдельные изображения. Это черный на белом. Я совершенно новичок в numpy,opencv&co - но вот моя текущая мысль:

• сканировать на черные пиксели
• найден черный пиксель -> водораздел
• найти границу водораздела (как путь многоугольника)
• продолжить поиск, но игнорировать точки в уже найденных границах

Я не очень хорош в таких вещах, есть ли лучший способ?

Сначала я попытался найти прямоугольную ограничивающую рамку результатов водораздела (это более или менее коллаж из примеров):

from numpy import *
import numpy as np
from scipy import ndimage

np.set_printoptions(threshold=np.nan)

a = np.zeros((512, 512)).astype(np.uint8) #unsigned integer type needed by watershed
y, x = np.ogrid[0:512, 0:512]
m1 = ((y-200)**2 + (x-100)**2 < 30**2)
m2 = ((y-350)**2 + (x-400)**2 < 20**2)
m3 = ((y-260)**2 + (x-200)**2 < 20**2)
a[m1+m2+m3]=1

markers = np.zeros_like(a).astype(int16)
markers[0, 0] = 1
markers[200, 100] = 2
markers[350, 400] = 3
markers[260, 200] = 4

res = ndimage.watershed_ift(a.astype(uint8), markers)
unique(res) 

B = argwhere(res.astype(uint8))
(ystart, xstart), (ystop, xstop) = B.min(0), B.max(0) + 1 
tr = a[ystart:ystop, xstart:xstop]

print tr

---

Каким-то образом, когда я использую исходный массив (a), кажется, что argwhere работает, но после водораздела (res) он просто снова выводит полный массив.

Следующим шагом может быть нахождение многоугольной траектории вокруг фигуры, но ограничивающая рамка была бы хороша сейчас!

Пожалуйста помоги!

Answer 1

@Hooked уже ответил на большинство ваших вопросов, но я был в процессе написания, когда он отвечал, поэтому я опубликую его в надежде, что это все еще полезно...

Вы пытаетесь прыгнуть через слишком много обручей. Вам не нужно watershed_ift,

Ты используешь scipy.ndimage.label различать отдельные объекты в логическом массиве и scipy.ndimage.find_objects найти ограничивающую рамку каждого объекта.

Давайте разберемся немного.

import numpy as np
from scipy import ndimage
import matplotlib.pyplot as plt

def draw_circle(grid, x0, y0, radius):
    ny, nx = grid.shape
    y, x = np.ogrid[:ny, :nx]
    dist = np.hypot(x - x0, y - y0)
    grid[dist < radius] = True
    return grid

# Generate 3 circles...
a = np.zeros((512, 512), dtype=np.bool)
draw_circle(a, 100, 200, 30)
draw_circle(a, 400, 350, 20)
draw_circle(a, 200, 260, 20)

# Label the objects in the array. 
labels, numobjects = ndimage.label(a)

# Now find their bounding boxes (This will be a tuple of slice objects)
# You can use each one to directly index your data. 
# E.g. a[slices[0]] gives you the original data within the bounding box of the
# first object.
slices = ndimage.find_objects(labels)

#-- Plotting... -------------------------------------
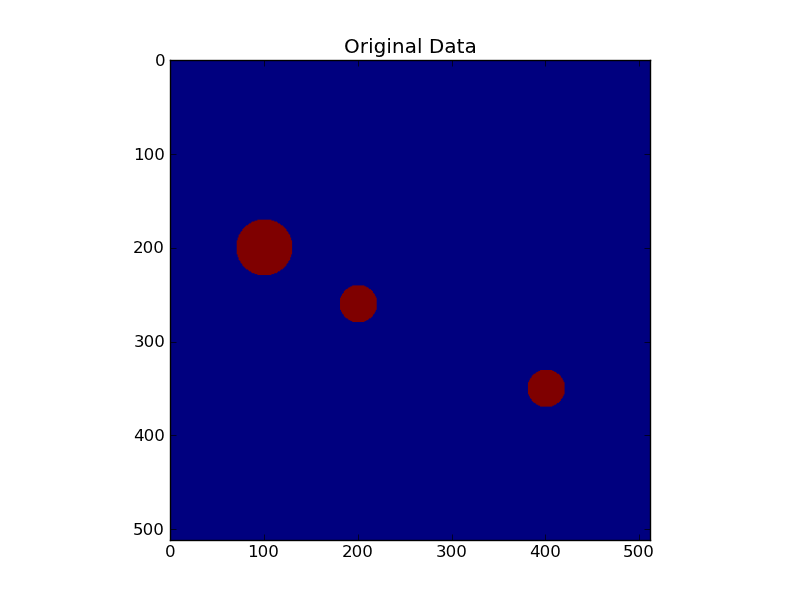
fig, ax = plt.subplots()
ax.imshow(a)
ax.set_title('Original Data')

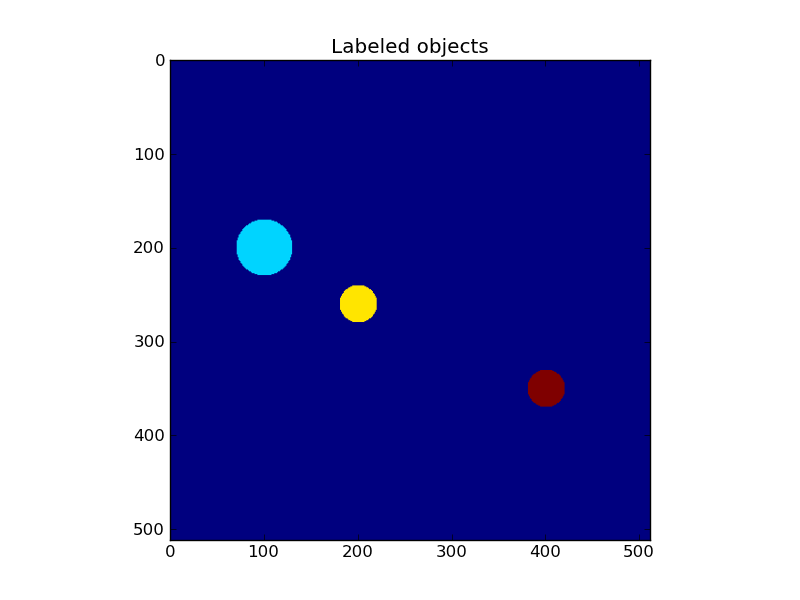
fig, ax = plt.subplots()
ax.imshow(labels)
ax.set_title('Labeled objects')

fig, axes = plt.subplots(ncols=numobjects)
for ax, sli in zip(axes.flat, slices):
    ax.imshow(labels[sli], vmin=0, vmax=numobjects)
    tpl = 'BBox:\nymin:{0.start}, ymax:{0.stop}\nxmin:{1.start}, xmax:{1.stop}'
    ax.set_title(tpl.format(*sli))
fig.suptitle('Individual Objects')

plt.show()

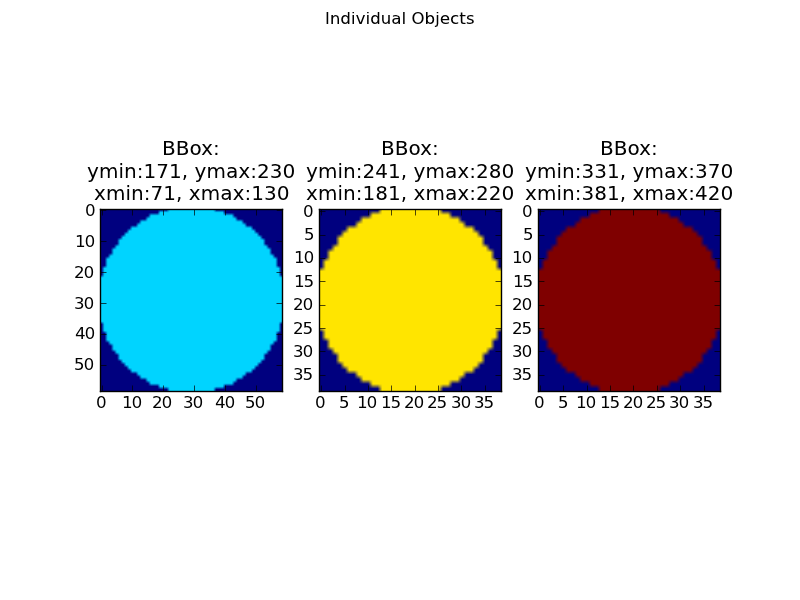
Надеюсь, это немного прояснит, как найти ограничивающие рамки объектов.

Answer 2

Использовать ndimage Библиотека от Сципи. Функция label размещает уникальный тег в каждом блоке пикселей, которые находятся в пределах порога. Это идентифицирует уникальные кластеры (формы). Начиная с вашего определения a:

from scipy import ndimage

image_threshold = .5
label_array, n_features =  ndimage.label(a>image_threshold)

# Plot the resulting shapes
import pylab as plt
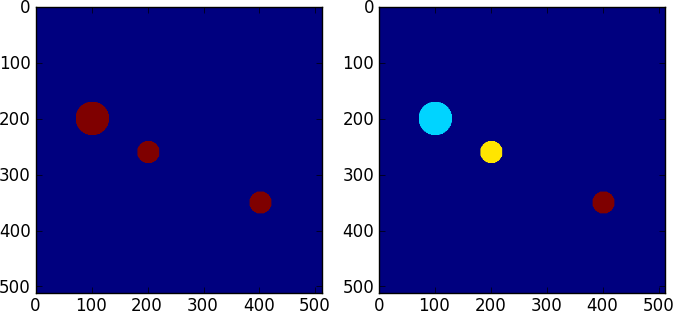
plt.subplot(121)
plt.imshow(a)
plt.subplot(122)
plt.imshow(label_array)
plt.show()