Запись музыкальных нот в файл WAV
Меня интересует, как брать музыкальные ноты (например, A, B, C# и т. Д.) Или аккорды (несколько нот одновременно) и записывать их в файл WAV.
Из того, что я понимаю, каждая нота имеет определенную частоту, связанную с ней (для идеального тона) - например, A4 (буква A выше среднего C) составляет 440 Гц (полный список 2/3 пути вниз на этой странице).
Если мое понимание верно, этот шаг находится в частотной области, и поэтому требуется ли применять к нему обратное быстрое преобразование Фурье для генерации эквивалента во временной области?
То, что я хочу знать, это:
- Как работают аккорды? Они средние из смол?
- Как определяется продолжительность воспроизведения каждой ноты, если содержимое файла wav представляет собой сигнал?
- Как результат преобразования нескольких заметок в обратное FFT-преобразование в массив байтов, которые составляют данные в файле WAV?
- любая другая соответствующая информация, относящаяся к этому.
Спасибо за любую помощь, которую вы можете оказать. Если приводить примеры кода, я использую C#, и код, который я сейчас использую для создания файлов WAV, выглядит следующим образом:
int channels = 1;
int bitsPerSample = 8;
//WaveFile is custom class to create a wav file.
WaveFile file = new WaveFile(channels, bitsPerSample, 11025);
int seconds = 60;
int samples = 11025 * seconds; //Create x seconds of audio
// Sound Data Size = Number Of Channels * Bits Per Sample * Samples
byte[] data = new byte[channels * bitsPerSample/8 * samples];
//Creates a Constant Sound
for(int i = 0; i < data.Length; i++)
{
data[i] = (byte)(256 * Math.Sin(i));
}
file.SetData(data, samples);
Это создает (как-то) постоянный звук - но я не совсем понимаю, как код соотносится с результатом.
3 ответа
Вы на правильном пути.
Давайте посмотрим на ваш пример:
for(int i = 0; i < data.Length; i++)
data[i] = (byte)(256 * Math.Sin(i));
ОК, у вас есть 11025 образцов в секунду. У вас есть образцы на 60 секунд. Каждый образец представляет собой число от 0 до 255, которое представляет собой небольшое изменение давления воздуха в точке пространства в данный момент времени.
Хотя, погоди, синус переходит от -1 к 1, поэтому сэмплы идут от -256 до +256, и это больше, чем диапазон байта, поэтому здесь происходит что-то глупое. Давайте переделаем ваш код, чтобы образец находился в нужном диапазоне.
for(int i = 0; i < data.Length; i++)
data[i] = (byte)(128 + 127 * Math.Sin(i));
Теперь у нас есть плавно изменяющиеся данные от 1 до 255, поэтому мы находимся в диапазоне байтов.
Попробуйте и посмотрите, как это звучит. Это должно звучать намного "гладко".
Человеческое ухо обнаруживает невероятно незначительные изменения давления воздуха. Если эти изменения образуют повторяющийся паттерн, то частота, с которой этот паттерн повторяется, интерпретируется улиткой в вашем ухе как особый тон. Величина изменения давления интерпретируется как объем.
Ваша форма волны составляет шестьдесят секунд. Изменение переходит от наименьшего изменения 1 к наибольшему изменению 255. Где находятся пики? То есть где образец достигает значения 255 или близко к нему?
Хорошо, синус равен 1 при π/2, 5π/2, 9π/2, 13π/2 и так далее. Так что пики всегда, когда я рядом с одним из них. То есть в 2, 8, 14, 20,...
Как далеко друг от друга во времени это? Каждый образец составляет 1/11025-ю секунды, поэтому пики составляют примерно 2/11025 = примерно 570 микросекунд между каждым пиком. Сколько пиков в секунду? 11025/2π = 1755 Гц. (Герц - это мера частоты; сколько пиков в секунду). 1760 Гц на две октавы выше А 440, так что это слегка плоский А-тон.
Как работают аккорды? Они средние из смол?
Нет. Аккорд А440 и октавы выше, A880 не эквивалентен 660 Гц. Вы не усредняете подачу. Вы суммируете форму волны.
Подумайте о давлении воздуха. Если у вас есть один вибрирующий источник, который нагнетает давление вверх и вниз 440 раз в секунду, и другой, который нагнетает давление вверх и вниз 880 раз в секунду, сеть будет отличаться от вибрации 660 раз в секунду. Это равно сумме давлений в любой данный момент времени. Помните, что все это WAV-файл: большой список изменений давления воздуха.
Предположим, вы хотите сделать октаву ниже вашего образца. Какая частота? В два раза меньше. Итак, давайте сделаем это вдвое реже:
for(int i = 0; i < data.Length; i++)
data[i] = (byte)(128 + 127 * Math.Sin(i/2.0));
Обратите внимание, что это должно быть 2.0, а не 2. Мы не хотим целочисленного округления! 2.0 сообщает компилятору, что вы хотите получить результат с плавающей запятой, а не целые числа.
Если вы сделаете это, вы получите пики вдвое реже: при i = 4, 16, 28... и, следовательно, тон будет на полную октаву ниже. (Каждая октава вниз уменьшает частоту вдвое; каждая октава увеличивает ее вдвое.)
Попробуйте это и посмотрите, как вы получите тот же тон, на октаву ниже.
Теперь сложите их вместе.
for(int i = 0; i < data.Length; i++)
data[i] = (byte)(128 + 127 * Math.Sin(i)) +
(byte)(128 + 127 * Math.Sin(i/2.0));
Это, вероятно, звучало как дерьмо. Что случилось? Мы снова переполнились; сумма была больше 256 во многих точках. Уменьшите вдвое объем обеих волн:
for(int i = 0; i < data.Length; i++)
data[i] = (byte)(128 + (63 * Math.Sin(i/2.0) + 63 * Math.Sin(i)));
Лучше. "63 sin x + 63 sin y" находится между -126 и +126, так что это не может переполнить байт.
(Таким образом, есть среднее значение: мы, по сути, берем среднее значение вклада в давление каждого тона, а не среднее значение частот.)
Если вы играете так, вы должны получить оба тона одновременно, один на октаву выше, чем другой.
Это последнее выражение сложно и трудно читать. Давайте разберем его на код, который легче читать. Но сначала подытожим историю:
- 128 находится на полпути между низким давлением (0) и высоким давлением (255).
- громкость звука - максимальное давление, достигаемое волной
- тон - это синусоида данной частоты
- частота в Гц - это частота дискретизации (11025), деленная на 2π
Итак, давайте соберем это вместе:
double sampleFrequency = 11025.0;
double multiplier = 2.0 * Math.PI / sampleFrequency;
int volume = 20;
// initialize the data to "flat", no change in pressure, in the middle:
for(int i = 0; i < data.Length; i++)
data[i] = 128;
// Add on a change in pressure equal to A440:
for(int i = 0; i < data.Length; i++)
data[i] = (byte)(data[i] + volume * Math.Sin(i * multiplier * 440.0)));
// Add on a change in pressure equal to A880:
for(int i = 0; i < data.Length; i++)
data[i] = (byte)(data[i] + volume * Math.Sin(i * multiplier * 880.0)));
И там вы идете; Теперь вы можете генерировать любой желаемый тон любой частоты и громкости. Чтобы создать аккорд, сложите их вместе, убедившись, что вы не слишком громкие и не переполняете байт.
Как узнать частоту ноты, отличную от A220, A440, A880 и т. Д.? Каждый полутон вверх умножает предыдущую частоту на 12-й корень из 2. Поэтому вычислите 12-й корень из 2, умножьте его на 440, и это A#. Умножьте A # на корень 12 из 2, то есть B. B, умноженный на 12-й корень из 2, это C, затем C# и так далее. Сделайте это 12 раз, и, поскольку это 12-й корень из 2, вы получите 880, вдвое больше, чем вы начали.
Как определяется продолжительность воспроизведения каждой ноты, если содержимое файла wav представляет собой сигнал?
Просто заполните пробное пространство, где звучит тон. Предположим, вы хотите сыграть А440 в течение 30 секунд, а затем A880 в течение 30 секунд:
// initialize the data to "flat", no change in pressure, in the middle:
for(int i = 0; i < data.Length; i++)
data[i] = 128;
// Add on a change in pressure equal to A440 for 30 seconds:
for(int i = 0; i < data.Length / 2; i++)
data[i] = (data[i] + volume * Math.Sin(i * multiplier * 440.0)));
// Add on a change in pressure equal to A880 for the other 30 seconds:
for(int i = data.Length / 2; i < data.Length; i++)
data[i] = (byte)(data[i] + volume * Math.Sin(i * multiplier * 880.0)));
Как результат преобразования нескольких заметок в обратное FFT-преобразование в массив байтов, которые составляют данные в файле WAV?
Обратное БПФ просто строит синусоиды и складывает их вместе, как мы делаем здесь. Вот и все!
любая другая соответствующая информация, касающаяся этого?
Смотрите мои статьи на эту тему.
http://blogs.msdn.com/b/ericlippert/archive/tags/music/
Части с первой по третью объясняют, почему у пианино двенадцать нот на октаву.
Часть четвертая относится к вашему вопросу; вот где мы создаем WAV-файл с нуля.
Обратите внимание, что в моем примере я использую 44100 выборок в секунду, а не 11025, и я использую 16-битные выборки с диапазоном от -16000 до +16000 вместо 8-битных выборок с диапазоном от 0 до 255. Но помимо этих деталей, это в основном так же, как у вас.
Я бы порекомендовал перейти на более высокую скорость передачи данных, если вы собираетесь использовать какой-либо сложный сигнал; 8 бит с частотой 11K выборок в секунду будут звучать ужасно для сложных сигналов. Качество 16 бит на семпл с частотой 44Кб в секунду.
И, честно говоря, намного проще понять математику, если вы делаете это в подписанных шортах, а не в беззнаковых байтах.
Часть пятая дает интересный пример слуховой иллюзии.
Кроме того, попробуйте просматривать свои волновые формы с помощью визуализации "scope" в проигрывателе Windows Media. Это даст вам хорошее представление о том, что на самом деле происходит.
ОБНОВИТЬ:
Я заметил, что при добавлении двух нот вместе вы можете получить шум, потому что переход между двумя осциллограммами слишком резкий (например, заканчивается в верхней части одной и начинается в нижней части следующей). Как можно преодолеть эту проблему?
Отличный дополнительный вопрос.
По сути, здесь происходит мгновенный переход от (скажем) высокого давления к низкому давлению, которое воспринимается как "поп". Есть несколько способов справиться с этим.
Техника 1: фазовый сдвиг
Один из способов состоит в том, чтобы "сдвинуть фазу" последующего тона на некоторое небольшое количество, чтобы разность между начальным значением последующего тона и конечным значением предыдущего тона. Вы можете добавить термин фазового сдвига следующим образом:
data[i] = (data[i] + volume * Math.Sin(phaseshift + i * multiplier * 440.0)));
Если фазовый сдвиг равен нулю, очевидно, это не изменится. Фазовый сдвиг 2π (или любой, даже кратный π) также не меняется, так как sin имеет период 2π. Каждое значение между 0 и 2π сдвигается, когда тон "начинается" немного дальше по волне.
Выяснить, что такое правильный сдвиг фазы, может быть немного сложно. Если вы прочтете мои статьи о генерации "непрерывно нисходящего" тона иллюзии Шепарда, вы увидите, что я использовал простое исчисление, чтобы убедиться, что все меняется непрерывно без каких-либо всплесков. Вы можете использовать аналогичные методы, чтобы выяснить, что такое правильный сдвиг, чтобы заставить популярность исчезнуть.
Я пытаюсь понять, как генерировать значение сдвига фаз. Правильно ли использовать "ArcSin(((первая выборка данных новой заметки) - (последняя выборка данных предыдущей заметки))/noteVolume)"?
Ну, первое, что нужно понять, это то, что не может быть "правильной стоимости". Если конечная нота очень громкая и заканчивается на пике, а начальная нота очень тихая, в новом тоне может не быть точки, соответствующей значению старого тона.
Предполагая, что есть решение, что это? У вас есть конечная выборка, назовите ее y, и вы хотите найти фазовый сдвиг x такой, что
y = v * sin(x + i * freq)
когда я ноль. Так вот
x = arcsin(y / v)
Однако это может быть не совсем правильно! Предположим, у вас есть
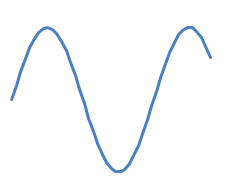
и вы хотите добавить
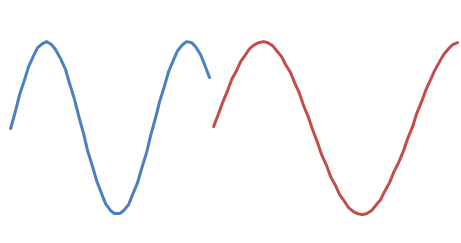
Есть два возможных сдвига фаз:
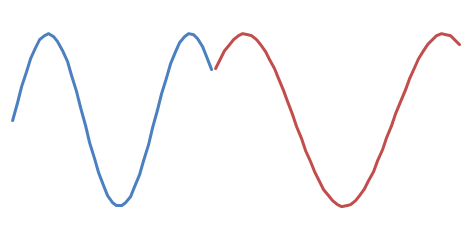
а также
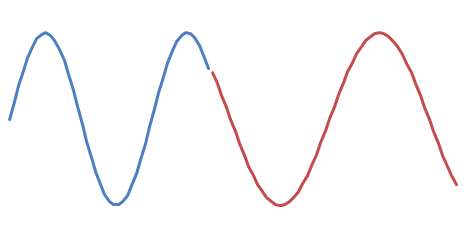
Думайте, какой из них звучит лучше.:-)
Выяснить, находитесь ли вы на "подъёме" или "подъёме" волны, может быть немного сложно. Если вы не хотите заниматься реальной математикой, вы можете сделать несколько простых эвристических операций, например, "изменился ли признак различия между последовательными точками данных при переходе?"
Техника 2: ADSR конверт
Если вы моделируете что-то, что должно звучать как настоящий инструмент, вы можете получить хорошие результаты, изменив громкость следующим образом.
То, что вы хотите сделать, это иметь четыре различных раздела для каждой ноты, называемые атака, затухание, сустейн и релиз. Громкость ноты, сыгранной на инструменте, может быть смоделирована следующим образом:
/\
/ \__________
/ \
/ \
A D S R
Громкость начинается с нуля. Затем происходит атака: звук быстро достигает максимальной громкости. Затем он немного разлагается до своего уровня поддержания. Затем он остается на этом уровне, возможно, медленно снижается во время воспроизведения ноты, а затем возвращается к нулю.
Если вы сделаете это, то всплывающего окна не будет, потому что начало и конец каждой ноты имеют нулевую громкость. Релиз гарантирует это.
Разные инструменты имеют разные "конверты". Трубный орган, например, имеет невероятно короткие атаки, разрушение и высвобождение; это все сустейн, а сустейн бесконечен. Ваш существующий код подобен органу. Сравните с, скажем, пианино. Снова короткая атака, короткое затухание, короткое освобождение, но звук постепенно становится тише во время сустейна.
Секции атаки, затухания и выпуска могут быть очень короткими, слишком короткими, чтобы их можно было услышать, но достаточно длинными, чтобы предотвратить появление. Поэкспериментируйте с изменением громкости во время воспроизведения ноты и посмотрите, что произойдет.
Ты на правильном пути.:)
Аудио сигнал
Вам не нужно делать обратное БПФ (вы могли бы, но вам нужно было бы найти для него библиотеку или реализовать ее, плюс генерировать сигнал в качестве входных данных). Намного проще получить ожидаемый результат от IFFT, который является синусоидальным сигналом с заданной частотой.
Аргумент синуса зависит как от сгенерированной ноты, так и от частоты дискретизации генерируемого вами волнового файла (часто равного 44100 Гц, в вашем примере вы используете 11025 Гц).
Для тона 1 Гц необходим синусоидальный сигнал с периодом, равным одной секунде. При частоте 44100 Гц частота дискретизации составляет 44100 в секунду, а это значит, что нам необходим синусоидальный сигнал с периодом, равным 44100 выборкам. Поскольку период синуса равен Тау (2* Пи), мы получаем:
sin(44100*f) = sin(tau)
44100*f = tau
f = tau / 44100 = 2*pi / 44100
Для 440 Гц мы получаем:
sin(44100*f) = sin(440*tau)
44100*f = 440*tau
f = 440 * tau / 44100 = 440 * 2 * pi / 44100
В C# это будет примерно так:
double toneFreq = 440d;
double f = toneFreq * 2d * Math.PI / 44100d;
for (int i = 0; i<data.Length; i++)
data[i] = (byte)(128 + 127*Math.Sin(f*i));
ПРИМЕЧАНИЕ: я не проверял это, чтобы проверить правильность кода. Я постараюсь сделать это и исправить любые ошибки.Обновление: я обновил код до чего-то, что работает. Извините за боль в ушах;-)
Аккорды
Аккорды - это комбинация нот (см., Например, Малый аккорд в Википедии). Таким образом, сигнал будет комбинацией (суммой) синусов с разными частотами.
Чистые тона
Эти тоны и аккорды не будут звучать естественно, потому что традиционные инструменты не воспроизводят одночастотные тоны. Вместо этого, когда вы играете на А4, наблюдается широкое распределение частот с концентрацией около 440 Гц. Смотрите, например, тембр.
Никто еще не упомянул алгоритм щипковых струн Karplus Strong.
Карплус - Сильный синтез струн. Это чрезвычайно простой метод для генерации реалистичного звучного струнного звука. Я написал полифонические музыкальные инструменты / MIDI-плееры в реальном времени, используя это.
Вы делаете это так:
Во-первых, какую частоту вы хотите симулировать? Допустим, концертный шаг А = 440 Гц
Предположим, что ваша частота дискретизации составляет 44,1 кГц, то есть 44100 / 440 = 100,25 выборок на длину волны.
Давайте округлим это до ближайшего целого числа: 100 и создадим кольцевой буфер длиной 100.
Таким образом, он будет удерживать одну стоячую волну с частотой ~440 Гц (заметьте, она не точная, есть способы обойти это).
Заполните его случайным статическим значением от -1 до +1, и:
DECAY = 0.99
while( n < 99999 )
outbuf[n++] = buf[k]
newVal = DECAY * ( buf[k] + buf_prev ) / 2
buf_prev = buf[k]
buf[k] = newVal
k = (k+1) % 100
Это удивительный алгоритм, потому что он очень прост и генерирует супер звук.
Лучший способ понять, что происходит, - это осознать, что случайная статика во временной области является белым шумом; случайная статика в частотной области. Вы можете представить его как композицию множества волн разной (случайной) частоты.
Частоты, близкие к 440 Гц (или 2*440 Гц, 3*440 Гц и т. Д.), Будут создавать конструктивные помехи для самих себя, поскольку они снова и снова проходят по кольцу. Так они будут сохранены. Другие частоты будут разрушительно мешать самим себе.
Кроме того, усреднение действует как фильтр нижних частот - представьте, что ваша последовательность равна +1 -1 +1 -1 +1 -1, если вы усредняете пары, тогда каждое среднее значение получается равным 0. Но если у вас более медленная волна, например 0 0,2 0,3 0,33 0,3 0,2... затем усреднение по-прежнему приводит к волне. Чем дольше волна, тем больше ее энергия сохраняется - т.е. усреднение вызывает меньшее затухание.
Таким образом, усреднение можно рассматривать как очень простой фильтр нижних частот.
Конечно, есть и сложности: необходимость выбора целочисленной длины буфера приводит к количественному определению возможных частот, что становится заметно ближе к вершине пианино. Все преодолимо, но становится трудно!
Ссылки:
Delicious Max / MSP Урок 1: Карплус-Стронг
Насколько я понимаю, JOS является ведущим мировым авторитетом в области генерации синтетических тонов, все дороги ведут на его сайт. Но имейте в виду, это очень сложно и требует математики университетского уровня.