Алгоритм обхода всех ребер графа

Question

Как личный пасхальный проект, я пытаюсь реализовать тестирование на основе моделей на работе. Я реализовал график в Python, и мне нужно пройти все ребра / сделать все переходы графа, по крайней мере, один раз. Обход ребра дважды или более не имеет значения, но мне нужно начать и закончить в одном и том же узле и получить последовательность ребер / переходов назад.

Более простой алгоритм> кратчайшая последовательность.

Я посмотрел вокруг и нашел много алгоритмов, но я не смог найти одну / комбинацию, которая работает для меня. Было бы здорово, если бы кто-то мог указать мне правильное направление или дать мне несколько советов, как это сделать.

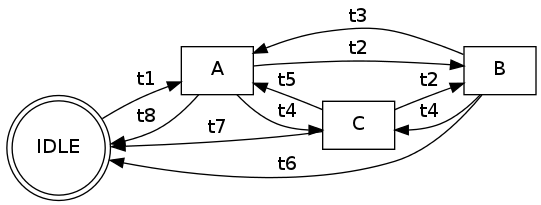
Моя реализация графа выглядит так:

graph = {
    A : {'IDLE': 't8', 'B': 't2', 'C': 't4'},
    B : {'A': 't3', 'C': 't4', 'IDLE': 't6'},
    C : {'A': 't5', 'IDLE': 't7', 'B': 't2'},
    IDLE : {'A': 't1'}
}

Answer 1

Подход 1

Вы можете изменить свой граф G на новый граф G', где каждое ребро в G становится узлом в G'. Сделайте ребро от t1 до t2 в G', если "A -> t1 -> B -> t2 -> C" возможно в G для некоторых A,B и C.

Тогда вам нужно найти покрытие пути в G'.

Подход 2

• Ваша позиция P изначально является некоторым узлом P0 (например, в режиме ожидания).
• Для каждого ребра T (от A до B) найдите любой маршрут от P до A, затем используйте T, чтобы перейти к B. Обновите P до B.
• Наконец, найдите любой маршрут от P до P0.

Answer 2

Эта проблема не совпадает с проблемой коммивояжера. Вместо этого это называется проблема китайского почтальона. Самое большое отличие состоит в том, что TSP хочет посетить все узлы (города), где CPP хочет посетить все края (улицы).

Идеальный учебник для именно этого можно найти здесь: https://www.datacamp.com/community/tutorials/networkx-python-graph-tutorial

Answer 3

Для каждой точки P1, точки P2 на вашем графике найдите все дороги R, где R выглядит следующим образом:

R = (P1, Pf1,..., Pfn, P2)

для каждой дороги R1, R2 от P1 до P2, если пересечение (R1, R2) имеет более 0 точек (кроме, конечно, P1 и P2), определить, какая из них короче. Если длина R1 меньше длины R2, тогда забудьте R2, в противном случае забудьте R1.

В итерации вы найдете самые короткие полностью отдельные дороги от P1 до P2. Если вы хотите пересечь дорогу, где у вас есть точки (P1, ..., Pk) Если мы выберем Pi, где 1<= i <= k, мы знаем, что первая точка будет Pi, а последняя точка будет также быть Пи.

Предположим, что порядок не имеет значения. Всякий раз, когда вы проходите точку, пометьте ее как пройденную. Если точка помечена как пройденная, вам не захочется снова идти к данной точке, но вы не будете возражать пересечь эту точку при необходимости. Итак, запланированная дорога будет: Pf1, ..., Pfk, Pf1.

для каждого Pfj, Pfm:

В данный момент мы находимся в Пфдж. Если Pfm пройден, мы не хотим снова переходить на Pfm, поэтому мы переходим к следующей итерации

Если Pfm не пройден, у нас есть дороги R1, ..., Rq из Pfj в Pfm. Выберите дорогу с максимальным количеством непересекающихся точек и минимальным количеством уже пройденных дорог. Вам нужно взвесить важность непересекаемого пункта на дороге и пройденного пункта с помощью умной идеи (надеюсь, ваш вес сведет к минимуму общую длину вашей дороги от Pf1 до Pf1).

Обратите внимание, что Pf1 не должен быть помечен как пройденный, потому что вы хотите прийти туда в конце вашего алгоритма.

Answer 4

Я не уверен, что вам нужен алгоритм или вы хотите знать, как выполнить свою работу. Если позже, вы можете использовать networkx.

После того, как вы загрузили и установили networkx, вы можете попробовать следующее

>>> import networkx as nx
>>> DG=nx.DiGraph()
>>> def CycleFrom(G,node):
    return sorted((c for c in nx.simple_cycles(DG) if node in c), key=len)[0]

>>> for (stnode, edges) in graph.items():
    for (ennode,edge) in edges.items():
        DG.add_edge(stnode,ennode,name=edge)


>>> for node in DG.nodes():
    print "Cycles from {0} is {1}".format(node,CycleFrom(DG,node))


Cycles from A is ['A', 'IDLE', 'A']
Cycles from IDLE is ['A', 'IDLE', 'A']
Cycles from B is ['A', 'B', 'A']
Cycles from C is ['A', 'C', 'A']
>>>