Как добавить несколько ограничений для diff_evolution?

Question

У меня та же проблема, что и в этом вопросе, но я не хочу добавлять только одно, но несколько ограничений к проблеме оптимизации.

Так, например, я хочу максимизировать x1 + 5 * x2 с ограничениями, что сумма x1 а также x2 меньше чем 5 а также x2 меньше чем 3 (Излишне говорить, что настоящая проблема гораздо сложнее и не может быть просто брошена в scipy.optimize.minimize как этот; это просто служит для иллюстрации проблемы...).

Я могу к такому уродливому хаку, как это:

from scipy.optimize import differential_evolution
import numpy as np

def simple_test(x, more_constraints):

    # check wether all constraints evaluate to True
    if all(map(eval, more_constraints)):

        return -1 * (x[0] + 5 * x[1])

    # if not all constraints evaluate to True, return a positive number
    return 10

bounds = [(0., 5.), (0., 5.)]

additional_constraints = ['x[0] + x[1] <= 5.', 'x[1] <= 3']
result = differential_evolution(simple_test, bounds, args=(additional_constraints, ), tol=1e-6)
print(result.x, result.fun, sum(result.x))

Это напечатает

[ 1.99999986  3.        ] -16.9999998396 4.99999985882

как и следовало ожидать.

Есть ли лучший / более простой способ добавить несколько ограничений, чем использование довольно "опасного" eval?

Answer 1

Пример примерно такой:

additional_constraints = [lambda(x): x[0] + x[1] <= 5., lambda(x):x[1] <= 3]

def simple_test(x, more_constraints):

    # check wether all constraints evaluate to True
    if all(constraint(x) for constraint in more_constraints):

        return -1 * (x[0] + 5 * x[1])

    # if not all constraints evaluate to True, return a positive number
    return 10

Answer 2

Принятый в настоящее время ответ описывает возможный взлом, но есть правильное решение проблемы, описанной в вопросе, для обеспечения соблюдения нескольких нелинейных ограничений с помощью scipy.optimize . Differential_evolution .

Правильный способ — использовать функцию scipy.optimize.NonlinearConstraint .

Ниже я привожу нетривиальный пример оптимизации классической функции Розенброка внутри области, определяемой пересечением двух окружностей.

      import numpy as np
from scipy import optimize

# Rosenbrock function
def fun(x):
    return 100*(x[1] - x[0]**2)**2 + (1 - x[0])**2

# Function defining the nonlinear constraints:
# 1) x^2 + (y - 3)^2 < 4
# 2) (x - 1)^2 + (y + 1)^2 < 13
def constr_fun(x):
    r1 = x[0]**2 + (x[1] - 3)**2
    r2 = (x[0] - 1)**2 + (x[1] + 1)**2
    return r1, r2

# No lower limit on constr_fun
lb = [-np.inf, -np.inf]

# Upper limit on constr_fun
ub = [4, 13]

# Bounds are irrelevant for this problem, but are needed
# for differential_evolution to compute the starting points
bounds = [[-2.2, 1.5], [-0.5, 2.2]]

nlc = optimize.NonlinearConstraint(constr_fun, lb, ub)
sol = optimize.differential_evolution(fun, bounds, constraints=nlc)

# Accurate solution by Mathematica
true = [1.174907377273171, 1.381484428610871]
print(f"nfev = {sol.nfev}")
print(f"x = {sol.x}")
print(f"err = {sol.x - true}\n")

Это печатает следующее с параметрами по умолчанию:

      nfev = 636
x = [1.17490808 1.38148613]
err = [7.06260962e-07 1.70116282e-06]

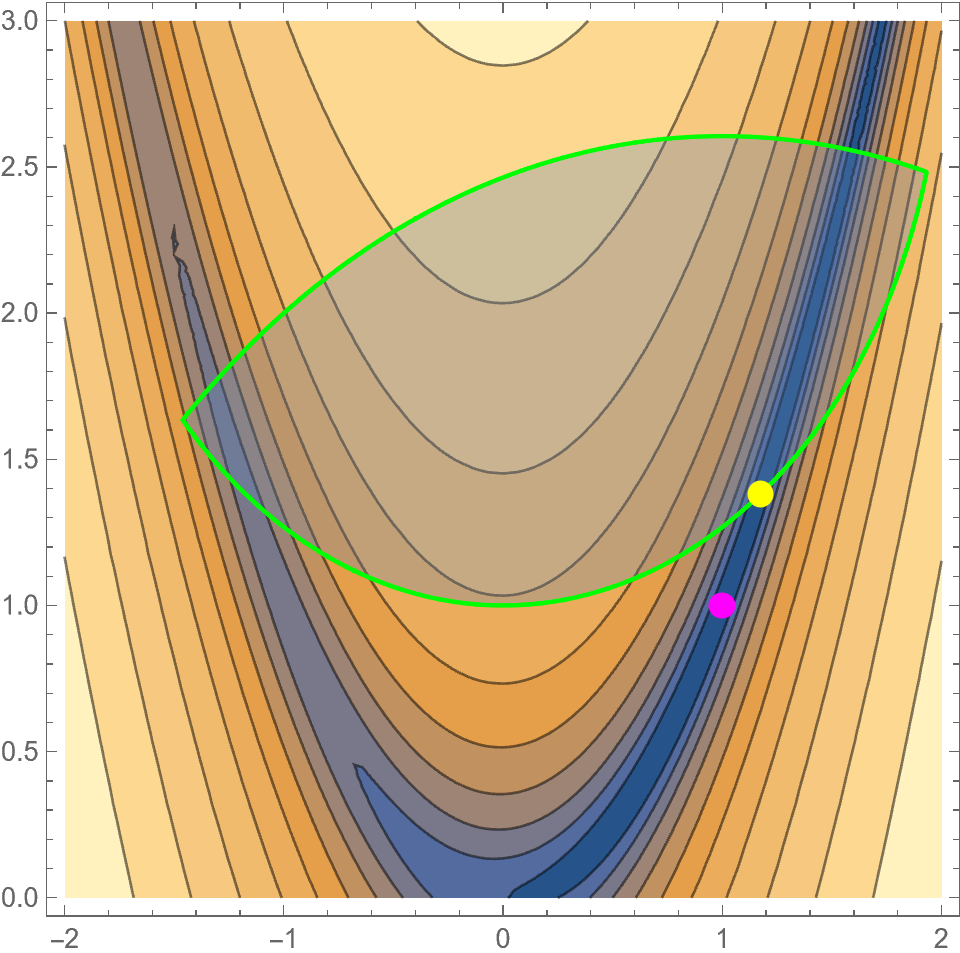
Вот визуализация функции (контуры) и допустимой области, определяемой нелинейными ограничениями (затенение внутри зеленой линии). Ограниченный глобальный минимум обозначен желтой точкой, а пурпурная точка показывает неограниченный глобальный минимум.

Эта задача с ограничениями имеет очевидный локальный минимум при (x, y) ~ (-1.2, 1.4)на границе допустимой области, из-за чего локальные оптимизаторы не смогут сходиться к глобальному минимуму для многих начальных местоположений. Однако, differential_evolutionпоследовательно находит глобальный минимум, как и ожидалось.