Python: перекрытие между двумя функциями (PDF kde и normal)
Краткое резюме: Я пытаюсь выяснить, как рассчитать перекрытие между двумя функциями. Один из них гауссовский, другой - плотность ядра, основанная на данных. Затем я хотел бы сделать небольшой алгоритм, который выбирает среднее значение и дисперсию для гауссиана, которая максимизирует перекрытие
Во-первых, необходим импорт:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats.kde import gaussian_kde
import scipy
У меня есть некоторые данные, которые являются приблизительно нормальными (несколько тяжелый правый хвост). Я вычисляю плотность ядра, cdf и pdf этих данных (в этом примере данные взяты из униформы, поскольку я не могу предоставить реальные данные) следующим образом:
def survivalFunction():
data = np.random.normal(7,1,100) #Random data
p = sns.kdeplot(data, shade=False, lw = 3)
x,y = p.get_lines()[0].get_data()
cdf = scipy.integrate.cumtrapz(y, x, initial=0)
plt.hist(data,50,normed = 1,facecolor='b',alpha = 0.3)
Тогда у меня есть другая функция, которая просто гауссовская:
def surpriseFunction(mu,variance):
hStates = np.linspace(0,20,100)
sigma = math.sqrt(variance)
plt.plot(hStates,scipy.stats.norm.pdf(hStates, mu, sigma))
вызывая функции
surpriseFunction(5,1)
survivalFunction()
дает этот сюжет
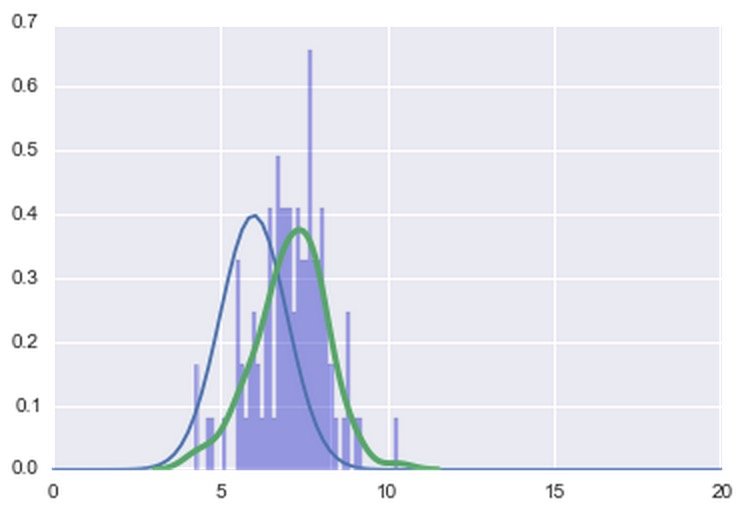
Как вы могли заметить, при обмене различными значениями mu происходит перемещение по нормали, чтобы более или менее перекрываться с оценкой ядра. Теперь мой вопрос состоит из двух частей:
1) Как рассчитать перекрытие между двумя функциями?
2) Как мне сделать небольшой алгоритм, который бы выбирал среднее и дисперсию для гауссиана таким образом, чтобы максимизировать это перекрытие?
1 ответ
Итак, я сделал довольно серьезную перестановку, я думаю, что она отделяет основные части и облегчит создание модульных / различных функций. Оригинальный код для предыдущего ответа, который я дал, здесь.
Вот новый материал, надеюсь, он довольно понятен.
# Setup our various global variables
population_mean = 7
population_std_dev = 1
samples = 100
histogram_bins = 50
# And setup our figure.
from matplotlib import pyplot
fig = pyplot.figure()
ax = fig.add_subplot(1,1,1)
from numpy.random import normal
hist_data = normal(population_mean, population_std_dev, samples)
ax.hist(hist_data, bins=histogram_bins, normed=True, color="blue", alpha=0.3)
from statsmodels.nonparametric.kde import KDEUnivariate
kde = KDEUnivariate(hist_data)
kde.fit()
#kde.supprt and kde.density hold the x and y values of the KDE fit.
ax.plot(kde.support, kde.density, color="red", lw=4)
#Gaussian function - though you can replace this with something of your choosing later.
from numpy import sqrt, exp, pi
r2pi = sqrt(2*pi)
def gaussian(x, mu, sigma):
return exp(-0.5 * ( (x-mu) / sigma)**2) / (sigma * r2pi)
#interpolation of KDE to produce a function.
from scipy.interpolate import interp1d
kde_func = interp1d(kde.support, kde.density, kind="cubic", fill_value=0)
То, что вы хотите сделать, - это просто стандартная подгонка кривой - есть множество способов сделать это, и вы говорите, что хотите подогнать кривую, максимизируя перекрытие двух функций (почему?). curve_fir подпрограмма scipy - это метод наименьших квадратов, который пытается минимизировать разницу между двумя функциями - разница невелика: максимальное перекрытие не наказывает функцию подгонки за то, что она больше, чем данные, тогда как curve_fit делает.
Я включил решения, использующие оба метода, а также профилировал их:
#We need to *maximise* the overlap integral
from scipy.integrate import quad as integrate
def overlap(func1, func2, limits, func1_args=[], func2_args=[]):
def product_func(x):
return min(func1(x, *func1_args),func2(x, *func2_args))
return integrate(product_func, *limits)[0] # we only care about the absolute result for now.
limits = hist_data.min(), hist_data.max()
def gaussian_overlap(args):
mu, sigma = args
return -overlap(kde_func, gaussian, limits, func2_args=[mu, sigma])
А теперь два разных метода, метрика перекрытия:
import cProfile, pstats, StringIO
pr1 = cProfile.Profile()
pr1.enable()
from scipy.optimize import fmin_powell as minimize
mu_overlap_fit, sigma_overlap_fit = minimize(gaussian_overlap, (population_mean, population_std_dev))
pr1.disable()
s = StringIO.StringIO()
sortby = 'cumulative'
ps = pstats.Stats(pr1, stream=s).sort_stats(sortby)
ps.print_stats()
print s.getvalue()
3122462 function calls in 6.298 seconds
Ordered by: cumulative time
ncalls tottime percall cumtime percall filename:lineno(function)
1 0.000 0.000 6.298 6.298 C:\Python27\lib\site-packages\scipy\optimize\optimize.py:2120(fmin_powell)
1 0.000 0.000 6.298 6.298 C:\Python27\lib\site-packages\scipy\optimize\optimize.py:2237(_minimize_powell)
57 0.000 0.000 6.296 0.110 C:\Python27\lib\site-packages\scipy\optimize\optimize.py:279(function_wrapper)
57 0.000 0.000 6.296 0.110 C:\Users\Will\Documents\Python_scripts\hist_fit.py:47(gaussian_overlap)
57 0.000 0.000 6.296 0.110 C:\Users\Will\Documents\Python_scripts\hist_fit.py:39(overlap)
57 0.000 0.000 6.296 0.110 C:\Python27\lib\site-packages\scipy\integrate\quadpack.py:42(quad)
57 0.000 0.000 6.295 0.110 C:\Python27\lib\site-packages\scipy\integrate\quadpack.py:327(_quad)
57 0.069 0.001 6.295 0.110 {scipy.integrate._quadpack._qagse}
66423 0.154 0.000 6.226 0.000 C:\Users\Will\Documents\Python_scripts\hist_fit.py:41(product_func)
4 0.000 0.000 6.167 1.542 C:\Python27\lib\site-packages\scipy\optimize\optimize.py:2107(_linesearch_powell)
4 0.000 0.000 6.166 1.542 C:\Python27\lib\site-packages\scipy\optimize\optimize.py:1830(brent)
4 0.000 0.000 6.166 1.542 C:\Python27\lib\site-packages\scipy\optimize\optimize.py:1887(_minimize_scalar_brent)
4 0.001 0.000 6.166 1.542 C:\Python27\lib\site-packages\scipy\optimize\optimize.py:1717(optimize)
и метод scipy curve_fit:
pr2 = cProfile.Profile()
pr2.enable()
from scipy.optimize import curve_fit
(mu_curve_fit, sigma_curve_fit), _ = curve_fit(gaussian, kde.support, kde.density, p0=(population_mean, population_std_dev))
pr2.disable()
s = StringIO.StringIO()
sortby = 'cumulative'
ps = pstats.Stats(pr2, stream=s).sort_stats(sortby)
ps.print_stats()
print s.getvalue()
122 function calls in 0.001 seconds
Ordered by: cumulative time
ncalls tottime percall cumtime percall filename:lineno(function)
1 0.000 0.000 0.001 0.001 C:\Python27\lib\site-packages\scipy\optimize\minpack.py:452(curve_fit)
1 0.000 0.000 0.001 0.001 C:\Python27\lib\site-packages\scipy\optimize\minpack.py:256(leastsq)
1 0.000 0.000 0.001 0.001 {scipy.optimize._minpack._lmdif}
19 0.000 0.000 0.001 0.000 C:\Python27\lib\site-packages\scipy\optimize\minpack.py:444(_general_function)
19 0.000 0.000 0.000 0.000 C:\Users\Will\Documents\Python_scripts\hist_fit.py:29(gaussian)
1 0.000 0.000 0.000 0.000 C:\Python27\lib\site-packages\scipy\linalg\basic.py:314(inv)
1 0.000 0.000 0.000 0.000 C:\Python27\lib\site-packages\scipy\optimize\minpack.py:18(_check_func)
Вы можете видеть, что метод curve_fit намного быстрее, и результаты:
from numpy import linspace
xs = linspace(-1, 1, num=1000) * sigma_overlap_fit * 6 + mu_overlap_fit
ax.plot(xs, gaussian(xs, mu_overlap_fit, sigma_overlap_fit), color="orange", lw=2)
xs = linspace(-1, 1, num=1000) * sigma_curve_fit * 6 + mu_curve_fit
ax.plot(xs, gaussian(xs, mu_curve_fit, sigma_curve_fit), color="purple", lw=2)
pyplot.show()

очень похожи Я бы посоветовал curve_fit, В этом случае это в 6000 раз быстрее. Разница немного больше, когда базовые данные более сложны, но не намного, и вы все еще получаете огромную скорость. Вот пример для 6 равномерно распределенных нормальных распределений:
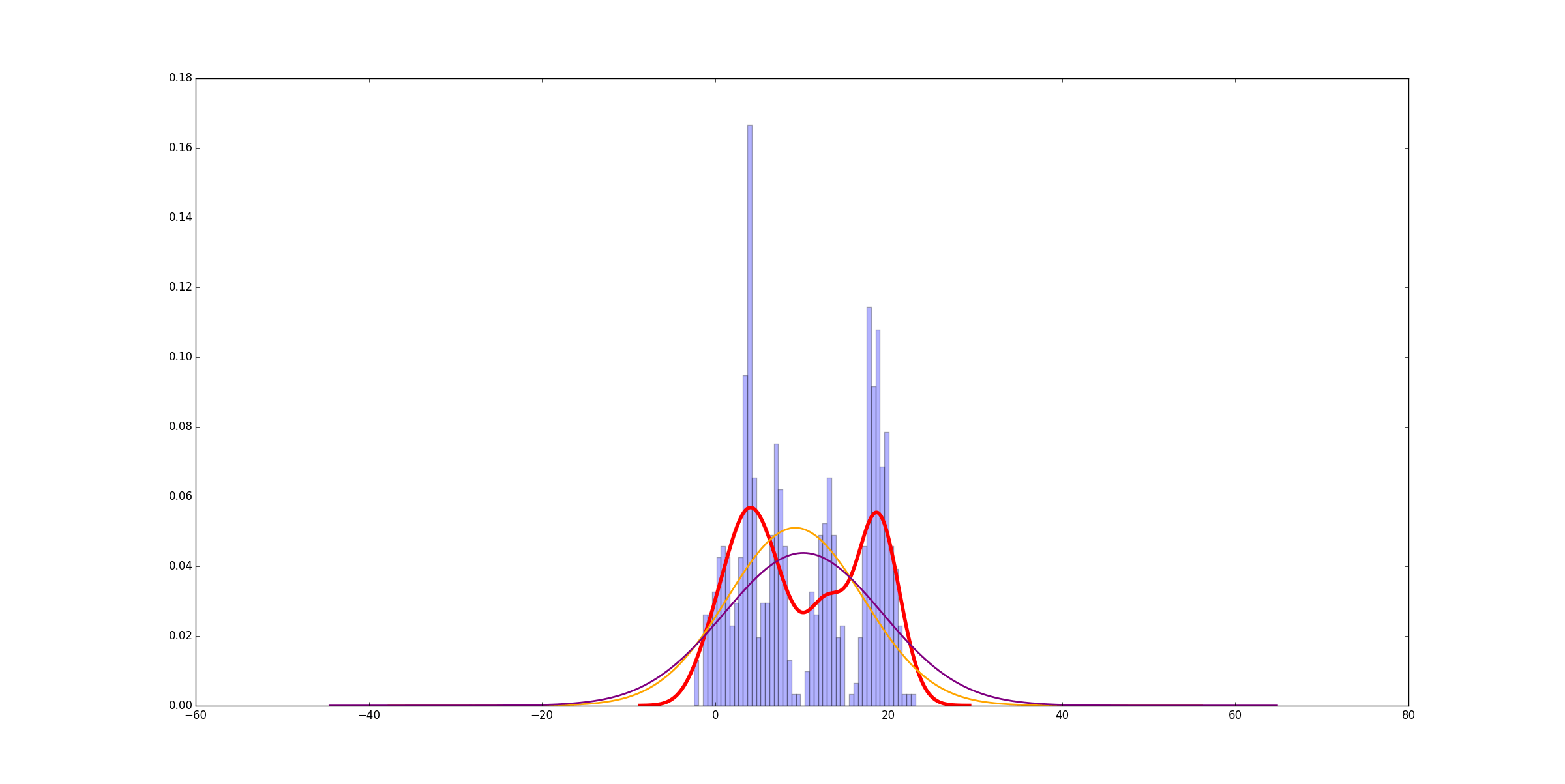
Идти с curve_fit!