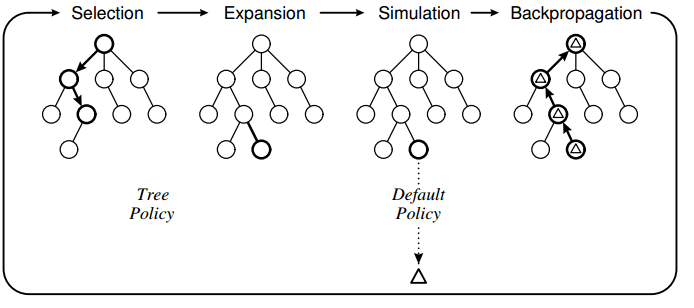
Как работает дерево поиска Монте-Карло?
Попытка изучить MCST, используя видео и документы YouTube, подобные этой.
http://www0.cs.ucl.ac.uk/staff/D.Silver/web/Applications_files/grand-challenge.pdf
Однако мне не очень повезло с пониманием деталей, выходящих за рамки теоретических объяснений высокого уровня. Вот некоторые цитаты из статьи выше и вопросы, которые у меня есть.
Этап выбора: MCTS итеративно выбирает дочерний узел с наибольшим количеством баллов текущего состояния. Если текущее состояние является корневым узлом, то откуда эти дети пришли в первую очередь? Разве у вас не было бы дерева с одним корневым узлом для начала? Имея только один корневой узел, вы сразу попадаете в фазу расширения и симуляции?
Если MCTS выбирает дочерний узел с наибольшим количеством баллов на этапе выбора, вы никогда не исследуете других дочерних узлов или, возможно, даже совершенно нового дочернего элемента, спускаясь по уровням дерева?
Как происходит фаза расширения для узла? На диаграмме выше, почему он не выбрал листовой узел, но решил добавить родного узла к листовому узлу?
На этапе симуляции стохастическая политика используется для выбора законных ходов для обоих игроков, пока игра не закончится. Является ли эта стохастическая политика жестко запрограммированным поведением, и вы, по сути, бросаете кубики в симуляции, чтобы выбрать один из возможных ходов по очереди между каждым игроком до конца?
Насколько я понимаю, вы начинаете с одного корневого узла и, повторяя описанные выше этапы, вы строите дерево до определенной глубины. Затем вы выбираете ребенка с лучшим результатом на втором уровне в качестве следующего шага. Размер дерева, которое вы хотите построить, в основном является вашим жестким требованием к отзывчивости ИИ, верно? Так как пока дерево строится, игра остановится и вычислит это дерево.
2 ответа
- Этап выбора: MCTS итеративно выбирает дочерний узел с наибольшим количеством баллов текущего состояния. Если текущее состояние является корневым узлом, то откуда эти дети пришли в первую очередь? Разве у вас не было бы дерева с одним корневым узлом для начала? Имея только один корневой узел, вы сразу попадаете в фазу расширения и симуляции?
Этап выбора, как правило, реализуется не для того, чтобы фактически выбирать узлы, которые действительно существуют в дереве (которые были созданы на этапе расширения). Обычно рекомендуется выбирать среди всех возможных преемников состояний игры, соответствующих вашему текущему узлу.
Таким образом, в самом начале, когда у вас есть только корневой узел, вы захотите, чтобы ваш шаг "Выбор" по-прежнему мог выбирать одно из всех возможных состояний игры-преемника (даже если у них нет соответствующих узлов в дереве). еще). Обычно вы хотите получить очень высокий балл (бесконечный или очень большую константу) для состояний игры, которые еще никогда не посещались (у которых еще нет узлов в дереве). Таким образом, ваш шаг выбора всегда будет случайным образом выбирать среди любых состояний, у которых еще нет соответствующего узла, и действительно использовать компромисс между разведкой и эксплуатацией только в тех случаях, когда все возможные игровые состояния уже имеют соответствующий узел в дереве,
- Если MCTS выбирает дочерний узел с наибольшим количеством баллов на этапе выбора, вы никогда не исследуете других дочерних узлов или, возможно, даже совершенно нового дочернего элемента, спускаясь по уровням дерева?
"Оценка", используемая на шаге "Выбор", обычно должна быть не просто средним значением всех результатов моделирования, проходящих через этот узел. Обычно это должен быть счет, состоящий из двух частей; часть "исследования", которая высока для узлов, которые посещались относительно редко, и часть "эксплуатации", которая высока для узлов, которые пока кажутся хорошими ходами (где многие симуляции, проходящие через этот узел, заканчивались победой для игрока, которому разрешено выбирать ход, чтобы сделать). Это описано в разделе 3.4 документа, который вы связали. W(s, a) / N(s, a) является частью эксплуатации (просто средний балл), а B(s, a) это разведочная часть.
- Как происходит фаза расширения для узла? На диаграмме выше, почему он не выбрал листовой узел, но решил добавить родного узла к листовому узлу?
Этап расширения обычно реализуется для простого добавления узла, соответствующего конечному состоянию игры, выбранному на этапе выбора (после того, как я ответил на ваш первый вопрос, на этапе выбора всегда заканчивается выбор одного состояния игры, которое никогда не было выбрано ранее).,
- На этапе симуляции стохастическая политика используется для выбора законных ходов для обоих игроков, пока игра не закончится. Является ли эта стохастическая политика жестко запрограммированным поведением, и вы, по сути, бросаете кубики в симуляции, чтобы выбрать один из возможных ходов по очереди между каждым игроком до конца?
Самая простая (и, вероятно, самая распространенная) реализация, действительно, должна играть совершенно случайно. Также возможно сделать это иначе. Например, вы можете использовать эвристику, чтобы создать уклон к определенным действиям. Как правило, полностью случайное воспроизведение выполняется быстрее, что позволяет вам запускать больше симуляций за одно и то же время обработки. Однако, как правило, это также означает, что каждая отдельная симуляция менее информативна, что означает, что вам действительно нужно запустить больше симуляций, чтобы MCTS играл хорошо.
- Насколько я понимаю, вы начинаете с одного корневого узла и, повторяя описанные выше этапы, вы строите дерево до определенной глубины. Затем вы выбираете ребенка с лучшим результатом на втором уровне в качестве следующего шага. Размер дерева, которое вы хотите построить, в основном является вашим жестким требованием к отзывчивости ИИ, верно? Так как пока дерево строится, игра остановится и вычислит это дерево.
MCTS не одинаково исследует все части дерева на одинаковую глубину. Он имеет тенденцию исследовать детали, которые кажутся интересными (сильные движения) глубже, чем детали, которые кажутся неинтересными (слабые движения). Поэтому, как правило, вы не будете использовать ограничение по глубине. Вместо этого вы должны использовать ограничение по времени (например, продолжать выполнение итераций до тех пор, пока вы не потратите 1 секунду, или 5 секунд, или 1 минуту, или любое другое время обработки), или ограничение количества итераций (например, позвольте ему запустить 10K или 50K или любое количество симуляций, которые вам нравятся).
По сути, Монте-Карло таков: попробуйте случайно много раз (*), а затем продолжайте движение, которое в большинстве случаев приводило к лучшему результату.
(*): количество раз и глубина зависит от скорости решения, которое вы хотите получить.
Таким образом, корневой узел всегда является текущим игровым состоянием, а вашими ближайшими детьми являются ваши возможные ходы. Если вы можете сделать 2 хода (да / нет, влево / вправо,...), то у вас есть 2 подузла.
Если вы не можете делать какие-либо ходы (это может произойти в зависимости от игры), тогда у вас нет никакого решения, поэтому Montec Carlo бесполезен для этого хода.
Если у вас есть X возможных ходов (игра в шахматы), то каждый возможный ход является прямым дочерним узлом.
Затем (в игре для 2 игроков) каждый уровень чередуется с "вашими ходами", "движениями противника" и так далее.
Как пройти дерево должно быть случайным (равномерным).
Ваш ход 1 (случайный ход подуровня 1)
Его ход 4 (случайный ход подуровня 2)
Ваш ход 3 (случайный ход подуровня 3) -> выиграть yay
Выберите опорную максимальную глубину и оцените, сколько раз вы выигрываете или проигрываете (или обладаете некоторой оценочной функцией, если игра не завершена после X глубины).
Вы повторяете операцию Y раз (будучи довольно большой) и выбираете непосредственный дочерний узел (он же ваш ход), который приводит к тому, что вы выигрываете большую часть времени.
Это чтобы оценить, какой шаг вы должны сделать сейчас. После этого противник двигается, и снова ваша очередь. Таким образом, вы должны воссоздать дерево с корневым узлом, являющимся новой текущей ситуацией, и переделать технику Монте-Карло, чтобы угадать, какой ваш лучший ход. И так далее.