Оценка области изображения, созданного набором точек (альфа-формы??)
У меня есть набор точек в примере файла ASCII, показывающий 2D-изображение.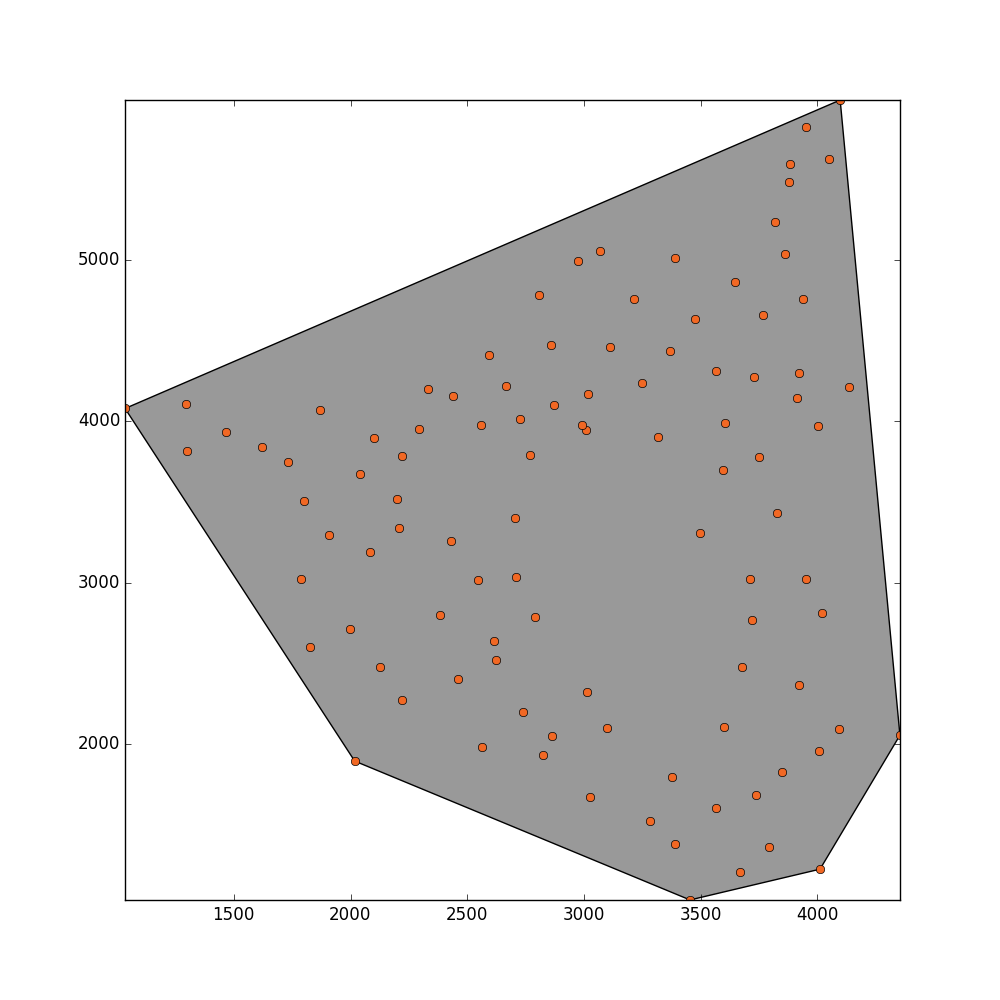 
Я хотел бы оценить общую площадь, которую заполняют эти точки. Есть некоторые места внутри этой плоскости, которые не заполнены ни одной точкой, потому что эти области были замаскированы. То, что я предполагаю, может быть практичным для оценки площади, будет применение вогнутой формы корпуса или альфа-формы. Я попробовал этот подход, чтобы найти подходящий alpha значение, и, следовательно, оценить площадь.
from shapely.ops import cascaded_union, polygonize
import shapely.geometry as geometry
from scipy.spatial import Delaunay
import numpy as np
import pylab as pl
from descartes import PolygonPatch
from matplotlib.collections import LineCollection
def plot_polygon(polygon):
fig = pl.figure(figsize=(10,10))
ax = fig.add_subplot(111)
margin = .3
x_min, y_min, x_max, y_max = polygon.bounds
ax.set_xlim([x_min-margin, x_max+margin])
ax.set_ylim([y_min-margin, y_max+margin])
patch = PolygonPatch(polygon, fc='#999999',
ec='#000000', fill=True,
zorder=-1)
ax.add_patch(patch)
return fig
def alpha_shape(points, alpha):
if len(points) < 4:
# When you have a triangle, there is no sense
# in computing an alpha shape.
return geometry.MultiPoint(list(points)).convex_hull
def add_edge(edges, edge_points, coords, i, j):
"""
Add a line between the i-th and j-th points,
if not in the list already
"""
if (i, j) in edges or (j, i) in edges:
# already added
return
edges.add( (i, j) )
edge_points.append(coords[ [i, j] ])
coords = np.array([point.coords[0]
for point in points])
tri = Delaunay(coords)
edges = set()
edge_points = []
# loop over triangles:
# ia, ib, ic = indices of corner points of the
# triangle
for ia, ib, ic in tri.vertices:
pa = coords[ia]
pb = coords[ib]
pc = coords[ic]
# Lengths of sides of triangle
a = np.sqrt((pa[0]-pb[0])**2 + (pa[1]-pb[1])**2)
b = np.sqrt((pb[0]-pc[0])**2 + (pb[1]-pc[1])**2)
c = np.sqrt((pc[0]-pa[0])**2 + (pc[1]-pa[1])**2)
# Semiperimeter of triangle
s = (a + b + c)/2.0
# Area of triangle by Heron's formula
area = np.sqrt(s*(s-a)*(s-b)*(s-c))
circum_r = a*b*c/(4.0*area)
# Here's the radius filter.
#print circum_r
if circum_r < 1.0/alpha:
add_edge(edges, edge_points, coords, ia, ib)
add_edge(edges, edge_points, coords, ib, ic)
add_edge(edges, edge_points, coords, ic, ia)
m = geometry.MultiLineString(edge_points)
triangles = list(polygonize(m))
return cascaded_union(triangles), edge_points
points=[]
with open("test.asc") as f:
for line in f:
coords=map(float,line.split(" "))
points.append(geometry.shape(geometry.Point(coords[0],coords[1])))
print geometry.Point(coords[0],coords[1])
x = [p.x for p in points]
y = [p.y for p in points]
pl.figure(figsize=(10,10))
point_collection = geometry.MultiPoint(list(points))
point_collection.envelope
convex_hull_polygon = point_collection.convex_hull
_ = plot_polygon(convex_hull_polygon)
_ = pl.plot(x,y,'o', color='#f16824')
concave_hull, edge_points = alpha_shape(points, alpha=0.001)
lines = LineCollection(edge_points)
_ = plot_polygon(concave_hull)
_ = pl.plot(x,y,'o', color='#f16824')
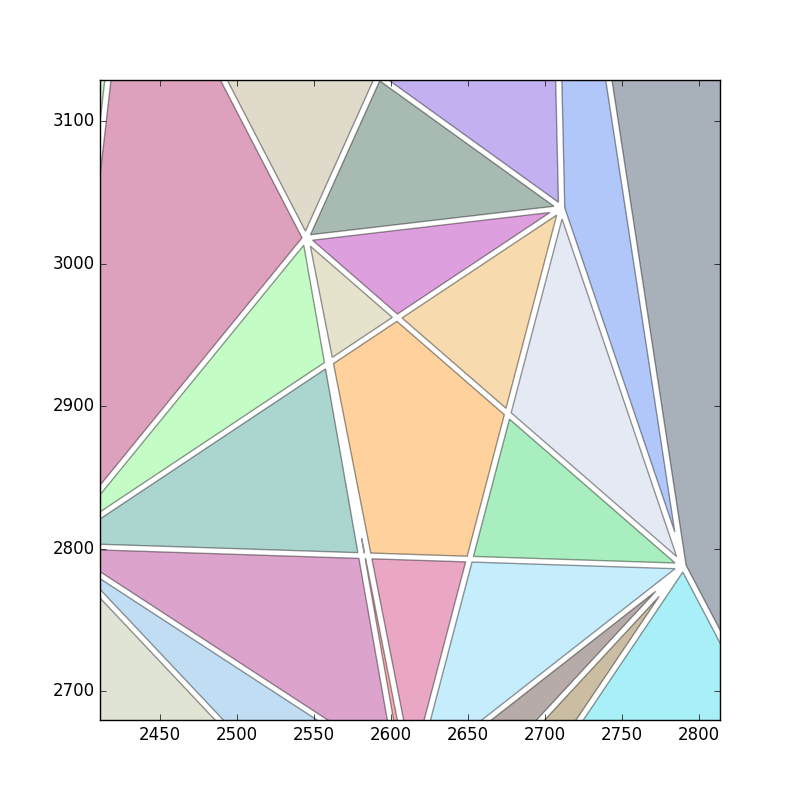
Я получаю этот результат, но я хотел бы, чтобы этот метод мог обнаружить дыру в середине.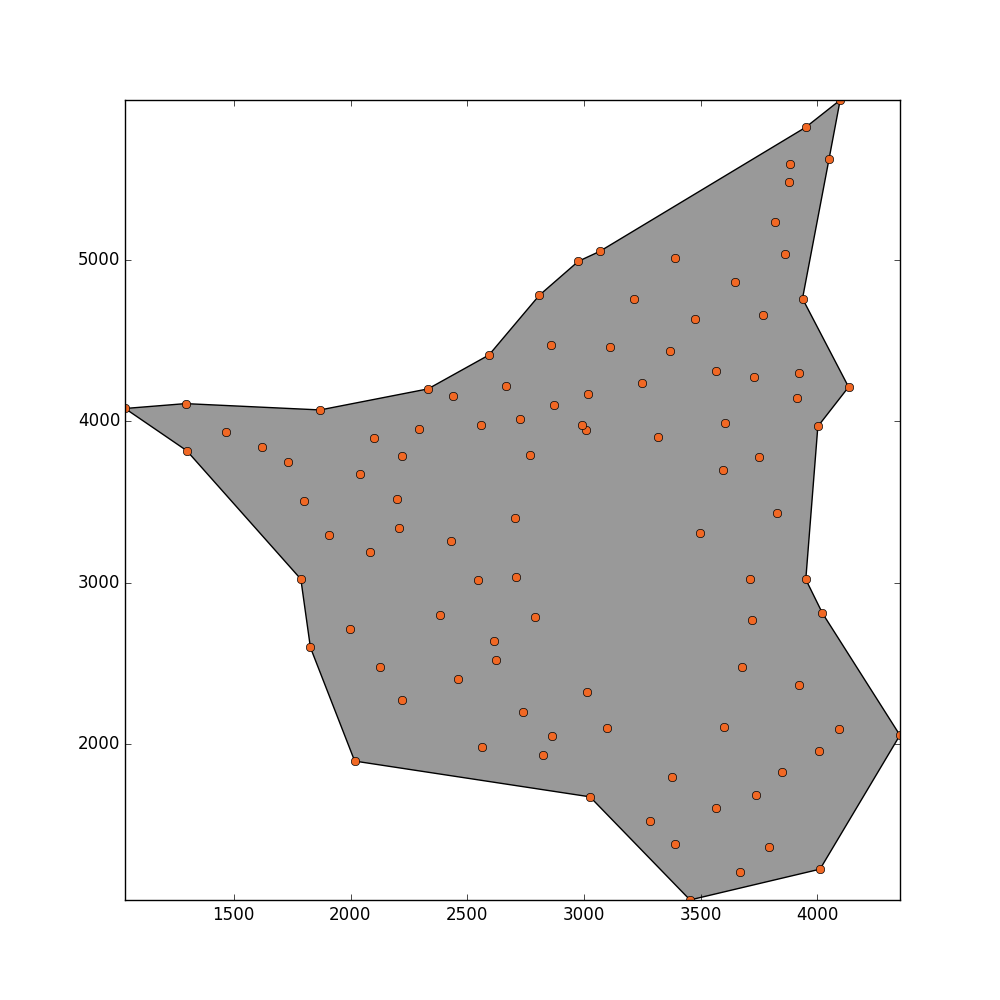 
Обновить
Вот как выглядят мои реальные данные: 
Мой вопрос: как лучше всего оценить площадь вышеупомянутой формы? Я не могу понять, что пошло не так, что этот код не работает должным образом?!! Любая помощь будет оценена.
4 ответа
Хорошо, вот идея. Триангуляция Делоне будет генерировать треугольники, которые являются неизбирательно большими. Это также будет проблематично, потому что будут генерироваться только треугольники.
Поэтому мы сгенерируем то, что вы могли бы назвать "нечеткой триангуляцией Делоне". Мы поместим все точки в kd-дерево и для каждой точки pпосмотри на его k ближайшие соседи. KD-дерево делает это быстро.
Для каждого из тех k соседи, найдите расстояние до фокуса p, Используйте это расстояние для генерации веса. Мы хотим, чтобы соседние точки были более предпочтительными, чем более отдаленные, поэтому экспоненциальная функция exp(-alpha*dist) уместно здесь. Используйте взвешенные расстояния, чтобы построить функцию плотности вероятности, описывающую вероятность рисования каждой точки.
Теперь возьмите из этого распределения большое количество раз. Ближайшие точки будут выбираться чаще, в то время как более отдаленные точки будут выбираться реже. Для нарисованной точки запишите, сколько раз она была нарисована для координационного центра. Результатом является взвешенный график, где каждое ребро на графике соединяет близлежащие точки и взвешивается по частоте выбора пар.
Теперь отбросим все ребра графа, вес которого слишком мал. Это точки, которые, вероятно, не связаны. Результат выглядит так:
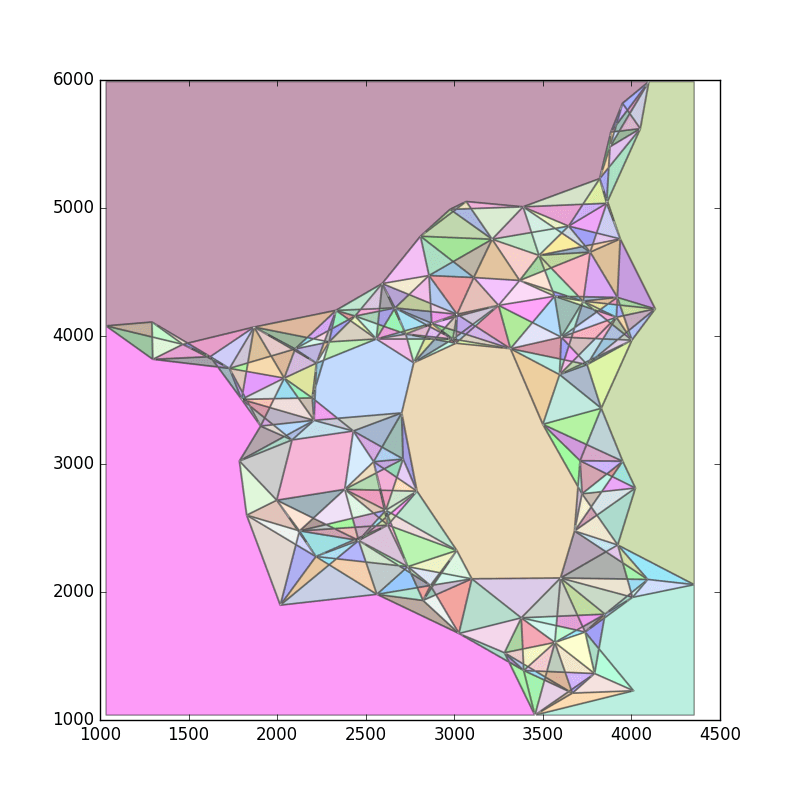
Теперь давайте бросим все остальные ребра в форму. Затем мы можем преобразовать ребра в очень маленькие многоугольники, буферизуя их. Вот так:
Дифференцирование полигонов с большим полигоном, покрывающим всю область, даст полигоны для триангуляции. Это может занять некоторое время Результат выглядит так:
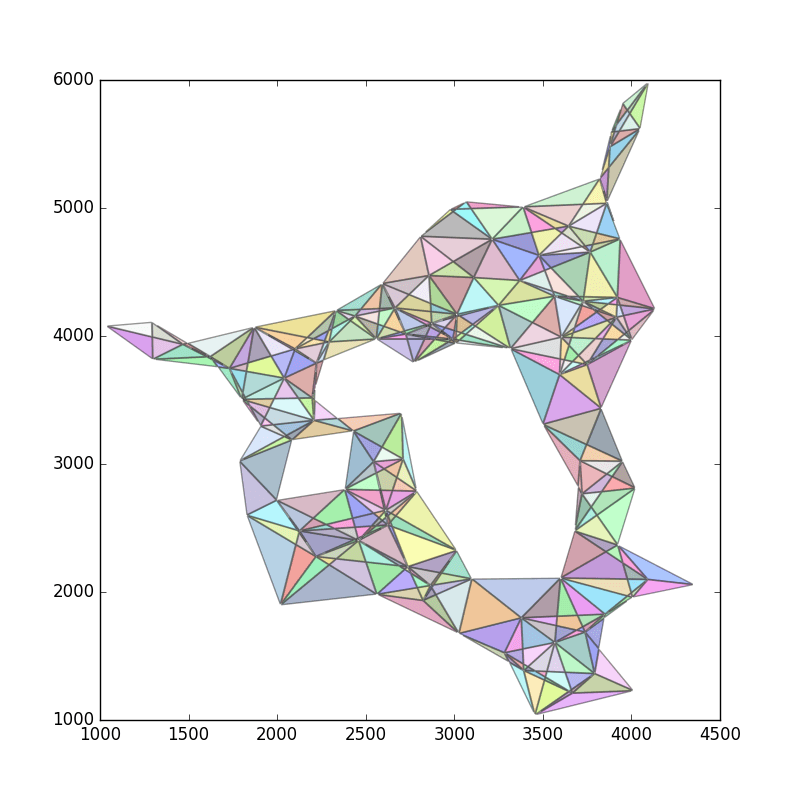
Наконец, отбросьте все слишком многоугольники:
#!/usr/bin/env python
import numpy as np
import matplotlib.pyplot as plt
import random
import scipy
import scipy.spatial
import networkx as nx
import shapely
import shapely.geometry
import matplotlib
dat = np.loadtxt('test.asc')
xycoors = dat[:,0:2]
xcoors = xycoors[:,0] #Convenience alias
ycoors = xycoors[:,1] #Convenience alias
npts = len(dat[:,0]) #Number of points
dist = scipy.spatial.distance.euclidean
def GetGraph(xycoors, alpha=0.0035):
kdt = scipy.spatial.KDTree(xycoors) #Build kd-tree for quick neighbor lookups
G = nx.Graph()
npts = np.max(xycoors.shape)
for x in range(npts):
G.add_node(x)
dist, idx = kdt.query(xycoors[x,:], k=10) #Get distances to neighbours, excluding the cenral point
dist = dist[1:] #Drop central point
idx = idx[1:] #Drop central point
pq = np.exp(-alpha*dist) #Exponential weighting of nearby points
pq = pq/np.sum(pq) #Convert to a PDF
choices = np.random.choice(idx, p=pq, size=50) #Choose neighbors based on PDF
for c in choices: #Insert neighbors into graph
if G.has_edge(x, c): #Already seen neighbor
G[x][c]['weight'] += 1 #Strengthen connection
else:
G.add_edge(x, c, weight=1) #New neighbor; build connection
return G
def PruneGraph(G,cutoff):
newg = G.copy()
bad_edges = set()
for x in newg:
for k,v in newg[x].items():
if v['weight']<cutoff:
bad_edges.add((x,k))
for b in bad_edges:
try:
newg.remove_edge(*b)
except nx.exception.NetworkXError:
pass
return newg
def PlotGraph(xycoors,G,cutoff=6):
xcoors = xycoors[:,0]
ycoors = xycoors[:,1]
G = PruneGraph(G,cutoff)
plt.plot(xcoors, ycoors, "o")
for x in range(npts):
for k,v in G[x].items():
plt.plot((xcoors[x],xcoors[k]),(ycoors[x],ycoors[k]), 'k-', lw=1)
plt.show()
def GetPolys(xycoors,G):
#Get lines connecting all points in the graph
xcoors = xycoors[:,0]
ycoors = xycoors[:,1]
lines = []
for x in range(npts):
for k,v in G[x].items():
lines.append(((xcoors[x],ycoors[x]),(xcoors[k],ycoors[k])))
#Get bounds of region
xmin = np.min(xycoors[:,0])
xmax = np.max(xycoors[:,0])
ymin = np.min(xycoors[:,1])
ymax = np.max(xycoors[:,1])
mls = shapely.geometry.MultiLineString(lines) #Bundle the lines
mlsb = mls.buffer(2) #Turn lines into narrow polygons
bbox = shapely.geometry.box(xmin,ymin,xmax,ymax) #Generate background polygon
polys = bbox.difference(mlsb) #Subtract to generate polygons
return polys
def PlotPolys(polys,area_cutoff):
fig, ax = plt.subplots(figsize=(8, 8))
for polygon in polys:
if polygon.area<area_cutoff:
mpl_poly = matplotlib.patches.Polygon(np.array(polygon.exterior), alpha=0.4, facecolor=np.random.rand(3,1))
ax.add_patch(mpl_poly)
ax.autoscale()
fig.show()
#Functional stuff starts here
G = GetGraph(xycoors, alpha=0.0035)
#Choose a value that rips off an appropriate amount of the left side of this histogram
weights = sorted([v['weight'] for x in G for k,v in G[x].items()])
plt.hist(weights, bins=20);plt.show()
PlotGraph(xycoors,G,cutoff=6) #Plot the graph to ensure our cut-offs were okay. May take a while
prunedg = PruneGraph(G,cutoff=6) #Prune the graph
polys = GetPolys(xycoors,prunedg) #Get polygons from graph
areas = sorted(p.area for p in polys)
plt.plot(areas)
plt.hist(areas,bins=20);plt.show()
area_cutoff = 150000
PlotPolys(polys,area_cutoff=area_cutoff)
good_polys = ([p for p in polys if p.area<area_cutoff])
total_area = sum([p.area for p in good_polys])
Вот мысль: используйте кластеризацию k-средних.
Вы можете сделать это в Python следующим образом:
from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt
dat = np.loadtxt('test.asc')
xycoors = dat[:,0:2]
fit = KMeans(n_clusters=2).fit(xycoors)
plt.scatter(dat[:,0],dat[:,1], c=fit.labels_)
plt.axes().set_aspect('equal', 'datalim')
plt.gray()
plt.show()
Используя ваши данные, это дает следующий результат:
Теперь вы можете взять выпуклый корпус верхнего кластера и нижнего кластера и рассчитать площади каждого отдельно. Добавление областей затем становится оценкой площади их объединения, но, как ни странно, избегает дыры в середине.
Чтобы точно настроить результаты, вы можете поиграть с количеством кластеров и количеством различных запусков алгоритма (алгоритм рандомизирован и обычно запускается более одного раза).
Вы, например, спросили, всегда ли два кластера покинут дыру в середине. Я использовал следующий код, чтобы поэкспериментировать с этим. Я генерирую равномерное распределение точек, а затем вырезаю эллипс произвольного размера и ориентирую его, чтобы смоделировать отверстие.
#!/usr/bin/env python3
import sklearn
import sklearn.cluster
import numpy as np
import matplotlib.pyplot as plt
PWIDTH = 6
PHEIGHT = 6
def GetPoints(num):
return np.random.rand(num,2)*300-150 #Centered about zero
def MakeHole(pts): #Chop out a randomly orientated and sized ellipse
a = np.random.uniform(10,150) #Semi-major axis
b = np.random.uniform(10,150) #Semi-minor axis
h = np.random.uniform(-150,150) #X-center
k = np.random.uniform(-150,150) #Y-center
A = np.random.uniform(0,2*np.pi) #Angle of rotation
surviving_points = []
for pt in range(pts.shape[0]):
x = pts[pt,0]
y = pts[pt,1]
if ((x-h)*np.cos(A)+(y-k)*np.sin(A))**2/a/a+((x-h)*np.sin(A)-(y-k)*np.cos(A))**2/b/b>1:
surviving_points.append(pt)
return pts[surviving_points,:]
def ShowManyClusters(pts,fitter,clusters,title):
colors = np.array([x for x in 'bgrcmykbgrcmykbgrcmykbgrcmyk'])
fig,axs = plt.subplots(PWIDTH,PHEIGHT)
axs = axs.ravel()
for i in range(PWIDTH*PHEIGHT):
lbls = fitter(pts[i],clusters)
axs[i].scatter(pts[i][:,0],pts[i][:,1], c=colors[lbls])
axs[i].get_xaxis().set_ticks([])
axs[i].get_yaxis().set_ticks([])
plt.suptitle(title)
#plt.show()
plt.savefig('/z/'+title+'.png')
fitters = {
'SpectralClustering': lambda x,clusters: sklearn.cluster.SpectralClustering(n_clusters=clusters,affinity='nearest_neighbors').fit(x).labels_,
'KMeans': lambda x,clusters: sklearn.cluster.KMeans(n_clusters=clusters).fit(x).labels_,
'AffinityPropagation': lambda x,clusters: sklearn.cluster.AffinityPropagation().fit(x).labels_,
}
np.random.seed(1)
pts = []
for i in range(PWIDTH*PHEIGHT):
temp = GetPoints(300)
temp = MakeHole(temp)
pts.append(temp)
for name,fitter in fitters.items():
for clusters in [2,3]:
np.random.seed(1)
ShowManyClusters(pts,fitter,clusters,"{0}: {1} clusters".format(name,clusters))
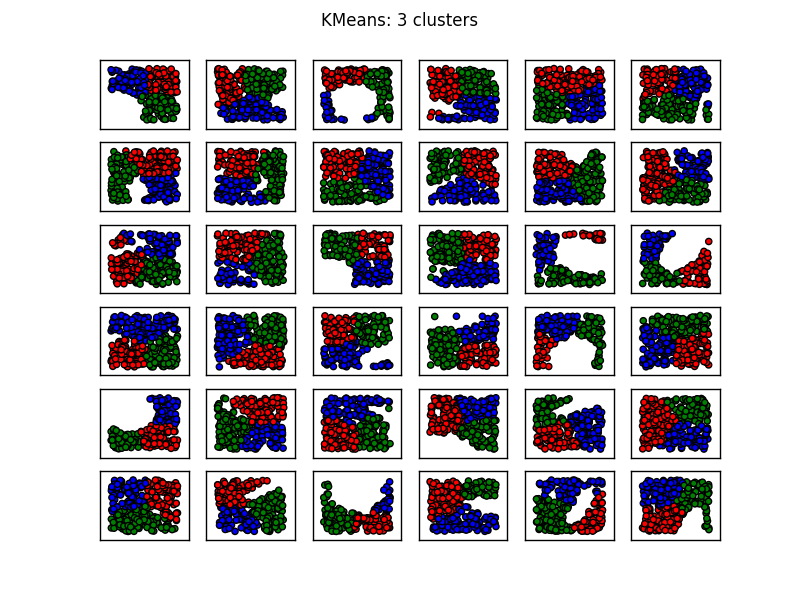
Рассмотрим результаты для K-Means:
По крайней мере, на мой взгляд, использование двух кластеров работает хуже, когда "дыра" разделяет данные на два отдельных объекта. (В этом случае это происходит, когда эллипс ориентирован так, что он перекрывает два ребра прямоугольной области, содержащей точки выборки.) Использование трех кластеров решает большинство из этих трудностей.
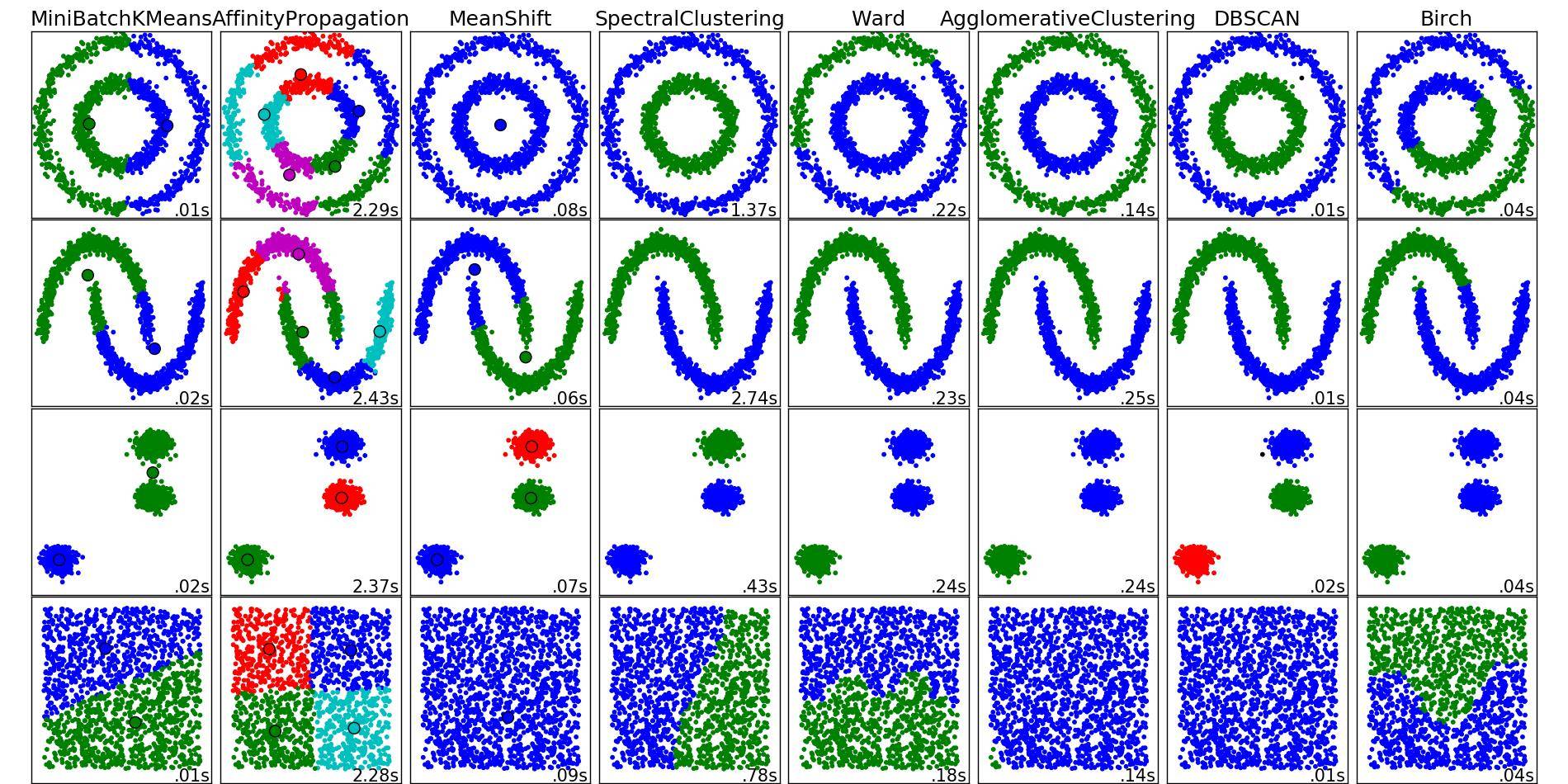
Вы также заметите, что K-means дает некоторые нелогичные результаты в 1-й колонке, 3-й строке, а также в 3-й колонке 4-й строки. Рассматривая зверинец склеарнских методов кластеризации, вы видите следующее изображение сравнения:
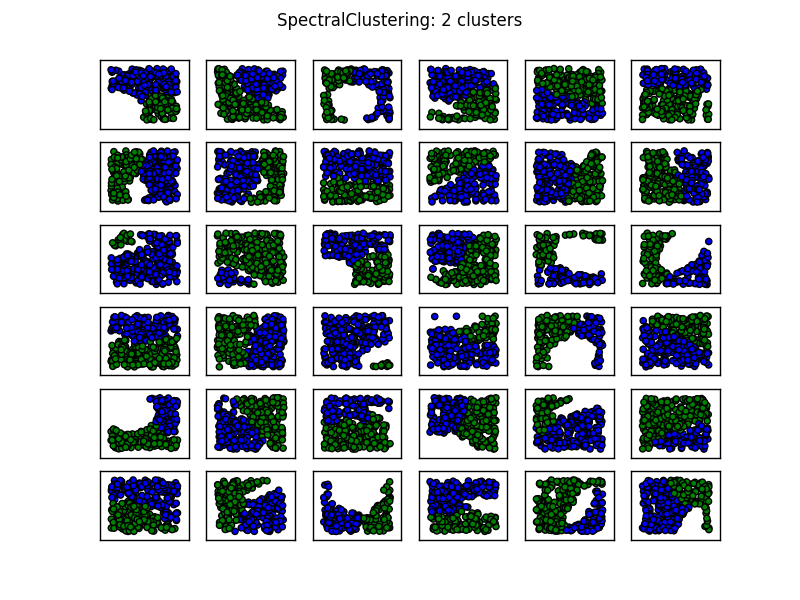
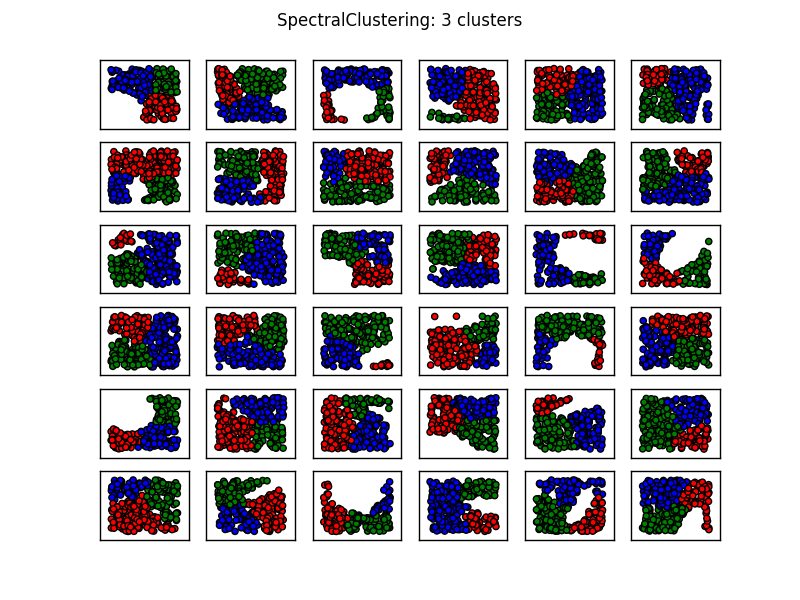
На этом изображении создается впечатление, что SpectralClustering дает результаты, которые соответствуют тому, что мы хотим. Попытка сделать это с теми же данными выше устраняет указанные проблемы (см. 1-й столбец, 3-й ряд и 3-й столбец, 4-й ряд).
Вышеизложенное предполагает, что спектральная кластеризация с тремя кластерами должна быть адекватной для большинства ситуаций такого рода.
Хотя вы, кажется, намереваетесь сделать вогнутую форму, вот альтернативный маршрут, который очень быстр, и я думаю, что вы получите очень стабильное чтение:
Создайте функцию, которая принимает в качестве аргумента (int radiusOfInfluence). Внутри функции запустите воксельный фильтр с радиусом. Затем просто умножьте площадь этого круга (pi*AOI^2) на количество оставшихся точек в облаке. Это должно дать вам относительно надежную оценку площади и будет очень устойчивым к отверстиям и странным краям.
Некоторые вещи для рассмотрения:
-Это даст вам положительное превышение площади из-за того, что края превышают ровно на один радиус. Модификацией для корректировки этого может быть запуск статистического фильтра удаления выбросов (в обратном режиме) для получения статистических граничных точек. Затем можно сделать предположение, что примерно половина каждой граничной точки лежит вне фигуры, вычтите половину числа точек, найденных из общего количества, до умножения на площадь.
- Радиус влияния в значительной степени определяет обнаружение отверстий в этой функции, так как более крупная точка позволит отдельным точкам покрывать большие области, но также с помощью настройки стандартного среза в фильтре выбросов выбросов можно более агрессивно обнаруживать внутренние отверстия и корректировать свою область таким образом.,
На самом деле напрашивается вопрос о том, к чему вы стремитесь, так как это скорее оценка точности снимка / типа группировки снимков, предполагающая разумно распределенный набор выборок. Ваш метод делает предположение, что ваши внешние граничные точки являются абсолютными пределами того, что возможно (что может быть справедливым предположением в зависимости от ситуации)
РЕДАКТИРОВАТЬ-----------------------
У меня нет времени написать пример кода, но я могу объяснить, чтобы помочь в понимании.
В основе этого лежит воксельный фильтр. Очень просто, он устанавливает начальную точку в координатах x,y, а затем создает сетку по всему пространству, которая имеет единицы измерения (интервал сетки) по обеим осям указанного пользователем радиуса фильтра. Внутри каждой ячейки сетки она будет усреднять все точки до одной точки. Это очень важно для этой концепции, потому что она почти полностью устраняет проблему наложения.
Вторая часть (обратное удаление статов) - это лишь небольшая хитрость для подгонки краев. По сути, статистические выбросы строятся для устранения шума путем рассмотрения расстояния от каждой точки до ее (k) ближайших соседей. После генерации среднего расстояния до k ближайших соседей для каждой точки он устанавливает гистограмму, а определяемый пользователем параметр действует как двоичный порог для сохранения или удаления точек. При инвертировании и установке на разумное значение среза (должно работать ~0,75 стандартного значения), вместо этого он удалит все точки, которые находятся в объеме объекта (т. Е. Только оставляя точки ребра). Это важно по той причине, что технически эти точки пересекают границу вашего объекта на 1 радиус. Хотя некоторые будут на остром, а некоторые на тупых углах кромки (то есть, больше или меньше, чем половина окружности переполнения), снимая половину площади круга на точку, следует над всем объектом дать вам довольно хорошее улучшение при подгонке кромки,
Имейте в виду, что в конце дня это просто даст вам номер. Что касается стресс-тестирования, я предлагаю создать искусственные облака точек известной области и создать графический вывод, показывающий, куда вы опускаете круги и полукруги (если вы хотите, ориентированные на внутреннюю часть объекта).
Ручки, которые вы захотите повернуть, чтобы улучшить этот метод: радиус фильтра Вокселя, область влияния на точку (фактически может управляться отдельно от радиуса фильтра вокс, хотя они должны оставаться довольно близко друг к другу), обрезание std.
Надеюсь, что это помогло уточнить, ура!
Редактировать:
Я заметил, что у вас есть свой собственный код для вычисления альфа-формы, и области треугольников Делоне как раз там, поэтому вычисление области формы еще проще...
Просто добавьте области треугольников, если треугольник будет добавлен к многоугольнику альфа-формы.
Если вы хотите обнаружить дыры... добавьте вторичный порог, чтобы избежать добавления треугольников с площадью, превышающей порог. Для этого примера значение max_area = 99999 удалит отверстие.
Единственная проблема - это способ создания графического вывода, потому что вы не увидите дыру.
def alpha_shape(points, alpha, max_area):
if len(points) < 4:
# When you have a triangle, there is no sense
# in computing an alpha shape.
return geometry.MultiPoint(list(points)).convex_hull , 0
def add_edge(edges, edge_points, coords, i, j):
"""
Add a line between the i-th and j-th points,
if not in the list already
"""
if (i, j) in edges or (j, i) in edges:
# already added
return
edges.add( (i, j) )
edge_points.append(coords[ [i, j] ])
coords = np.array([point.coords[0]
for point in points])
tri = Delaunay(coords)
total_area = 0
edges = set()
edge_points = []
# loop over triangles:
# ia, ib, ic = indices of corner points of the
# triangle
for ia, ib, ic in tri.vertices:
pa = coords[ia]
pb = coords[ib]
pc = coords[ic]
# Lengths of sides of triangle
a = np.sqrt((pa[0]-pb[0])**2 + (pa[1]-pb[1])**2)
b = np.sqrt((pb[0]-pc[0])**2 + (pb[1]-pc[1])**2)
c = np.sqrt((pc[0]-pa[0])**2 + (pc[1]-pa[1])**2)
# Semiperimeter of triangle
s = (a + b + c)/2.0
# Area of triangle by Heron's formula
area = np.sqrt(s*(s-a)*(s-b)*(s-c))
circum_r = a*b*c/(4.0*area)
# Here's the radius filter.
# print("radius", circum_r)
if circum_r < 1.0/alpha and area < max_area:
add_edge(edges, edge_points, coords, ia, ib)
add_edge(edges, edge_points, coords, ib, ic)
add_edge(edges, edge_points, coords, ic, ia)
total_area += area
m = geometry.MultiLineString(edge_points)
triangles = list(polygonize(m))
return cascaded_union(triangles), edge_points, total_area
Старый ответ:
Чтобы вычислить площадь нерегулярного простого многоугольника, вы можете использовать формулу Shoelace и координаты CCW границы в качестве входных данных.
Если вы хотите обнаружить дыры внутри вашего облака, вы должны удалить треугольники Делоне с радиусом окружности, превышающим вторичный порог. В идеале: вычислите триангуляцию Делоне и отфильтруйте по вашей текущей альфа-форме. Затем вычислите окружность каждого треугольника и удалите эти треугольники, у которых радиус окружности намного больше, чем у среднего.
Чтобы вычислить площадь неправильного многоугольника с отверстиями, используйте формулу Шнурка для каждой границы отверстия. Введите внешнюю границу в CCW (положительном) порядке, чтобы получить площадь. Затем введите границу каждого отверстия в непрерывном (отрицательном) порядке, чтобы получить (отрицательное) значение для площади.