Алгоритм проектирования - лучший способ найти наборы треугольников, которые разделяют вершину

Question

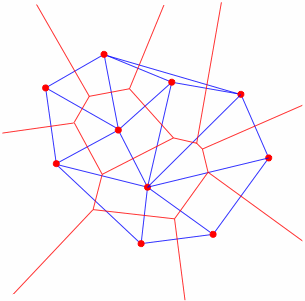
Я пытаюсь вычислить граф Вороного из триангуляции Делоне, у меня есть данные триангуляции в виде набора вершин (красные круги на графике) и треугольников (синие линии на графике):

Я могу легко вычислить вершины графа Вороного (пересечение красных линий), просто обведя центр всех треугольников.

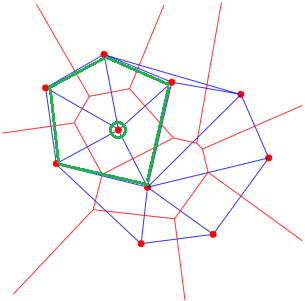
Тем не менее, мне нужно получить информацию о ячейке для каждого красного многоугольника. Чтобы сделать это, для каждой красной вершины мне нужно найти набор треугольников, которые разделяют ту же самую вершину. Итак, для обведенной вершины мне нужны зеленые треугольники:

Итак, мой код выглядит так (C#):

    foreach (Vertex3 vertex in DelaunayVertices)
    {
        VoronoiCell cell = new VoronoiCell();
        cell.Vertex = vertex;

        //seach all triangles for the ones that match this.
        foreach (Face3 face in DelaunayTriangles)
        {
            if (face.Vertices.Where(v => v.Equals(vertex)).Any())
            {
                //shares vertices, add it's circumcenter as an edge vertex of the cell
                cell.EdgeVertices.Add(face.Circumcenter);
            }
        }
    }

Что, конечно, крайне неэффективно, поскольку он ищет все. Тем не менее, коллекции лиц или вершин полностью не отсортированы (и я не уверен, как именно их отсортировать, или если это поможет). Просто чтобы запутать, на поверхности сферы есть 3-мерная вершина.

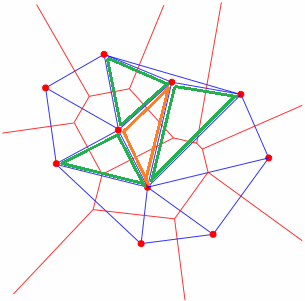
Единственное, что мне нужно, это найти смежные вершины или грани для каждого имеющегося у меня треугольника, это смежность, поэтому для оранжевого треугольника ниже я знаю три зеленых треугольника:

Я думаю, что было бы более эффективно обходить этот график, но я изо всех сил пытаюсь найти подход к алгоритму, который будет производить наборы, которые разделяют точки.

Answer 1

Если вы хотите сохранить вторичную структуру данных от вершины к треугольнику, вы можете сначала просмотреть список треугольников, поместив каждый треугольник в списки смежности, связанные с его тремя вершинами:

for (all tria's ti)
    for (all nodes ni in tria ti)
        v2t[ni] <- ti
    end for
end for

Это просто O(n) подметать.

Answer 2

Вы можете попробовать заполнить пространство кривой, то есть отсортировать вершины вдоль кривой Гильберта. Вы также можете попробовать провести тест на точку-полигон, но это очень сложно. Вы также можете попытаться создать растровое изображение с помощью алгоритма перебора.