Сглаживание двумерной фигуры

Question

У меня есть несколько смутно прямоугольных 2D фигур, которые нужно сгладить. Упрощенный пример:

fig, ax1 = plt.subplots(1,1, figsize=(3,3))
xs1 = [-0.25,  -0.625, -0.125, -1.25, -1.125, -1.25, 0.875, 1.0, 1.0, 0.5, 1.0, 0.625, -0.25]
ys1 = [1.25, 1.375, 1.5, 1.625, 1.75, 1.875, 1.875, 1.75, 1.625, 1.5, 1.375, 1.25, 1.25]

ax1.plot(xs1, ys1)
ax1.set_ylim(0.5,2.5)
ax1.set_xlim(-2,2) ;

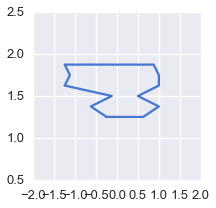
Я пробовал scipy.interpolate.RectBivariateSpline, но, по-видимому, для этого нужны данные во всех точках (например, для тепловой карты) и scipy.interpolate.interp1d, но для этого достаточно разумно сгенерировать 1d сглаженную версию.

Что является подходящим методом, чтобы сгладить это?

Изменить, чтобы пересмотреть / объяснить мою цель немного лучше. Мне не нужны линии, чтобы пройти все пункты; на самом деле, я бы предпочел, чтобы они не проходили все пункты, потому что есть явные выбросы, которые "должны" быть усреднены с соседями, или какой-то подобный подход. Я включил грубый ручной набросок начала того, что я имею в виду выше.

Answer 1

Алгоритм обрезки углов Чайкина может быть идеальным подходом для вас. Для данного многоугольника с вершинами как P0, P1, ...P(N-1) алгоритм разрезания углов будет генерировать 2 новые вершины для каждого отрезка, определенного P (i) и P(i+1) как

Q (i) = (3/4) P (i) + (1/4) P(i+1)
R (i) = (1/4) P (i) + (3/4) P(i+1)

Итак, ваш новый многоугольник будет иметь 2N вершин. Затем вы можете повторно и многократно накладывать резку углов на новый многоугольник, пока не будет достигнуто желаемое разрешение. Результатом будет многоугольник со многими вершинами, но они будут выглядеть гладкими при отображении. Можно доказать, что результирующая кривая, полученная из этого подхода резки углов, сойдется в квадратную кривую B-сплайна. Преимущество этого подхода в том, что результирующая кривая никогда не переиграет. Следующие фотографии помогут вам лучше понять этот алгоритм (фотографии взяты по этой ссылке)

Оригинальный полигон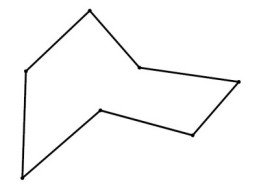

Применить угол резки один раз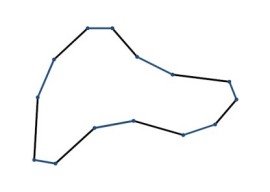

Примените угловое сокращение еще раз

Смотрите эту ссылку для более подробной информации об алгоритме резки углов Чайкина.

Answer 2

На самом деле, вы можете использовать scipy.interpolate.inter1d за это. Вы должны рассматривать компоненты x и y вашего многоугольника как отдельные серии.

В качестве быстрого примера с квадратом:

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d

x = [0, 1, 1, 0, 0]
y = [0, 0, 1, 1, 0]

t = np.arange(len(x))
ti = np.linspace(0, t.max(), 10 * t.size)

xi = interp1d(t, x, kind='cubic')(ti)
yi = interp1d(t, y, kind='cubic')(ti)

fig, ax = plt.subplots()
ax.plot(xi, yi)
ax.plot(x, y)
ax.margins(0.05)
plt.show()

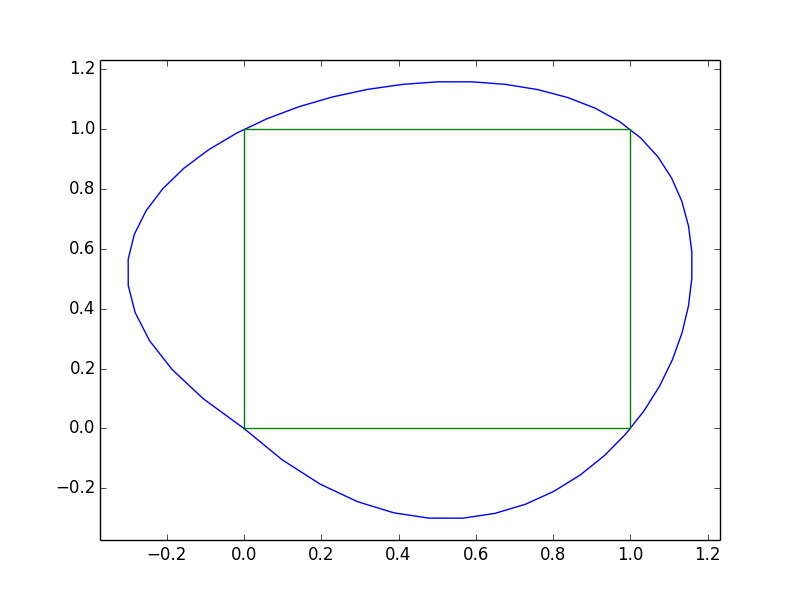
Однако, как вы можете видеть, это приводит к некоторым проблемам в 0,0.

Это происходит потому, что сплайн-сегмент зависит не только от двух точек. Первый и последний пункты не "связаны" так, как мы интерполировали. Мы можем исправить это, "дополнив" последовательности x и y второй и последней точками и вторыми точками, чтобы в конечных точках имелись граничные условия "обтекания" для сплайна.

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d

x = [0, 1, 1, 0, 0]
y = [0, 0, 1, 1, 0]

# Pad the x and y series so it "wraps around".
# Note that if x and y are numpy arrays, you'll need to
# use np.r_ or np.concatenate instead of addition!
orig_len = len(x)
x = x[-3:-1] + x + x[1:3]
y = y[-3:-1] + y + y[1:3]

t = np.arange(len(x))
ti = np.linspace(2, orig_len + 1, 10 * orig_len)

xi = interp1d(t, x, kind='cubic')(ti)
yi = interp1d(t, y, kind='cubic')(ti)

fig, ax = plt.subplots()
ax.plot(xi, yi)
ax.plot(x, y)
ax.margins(0.05)
plt.show()

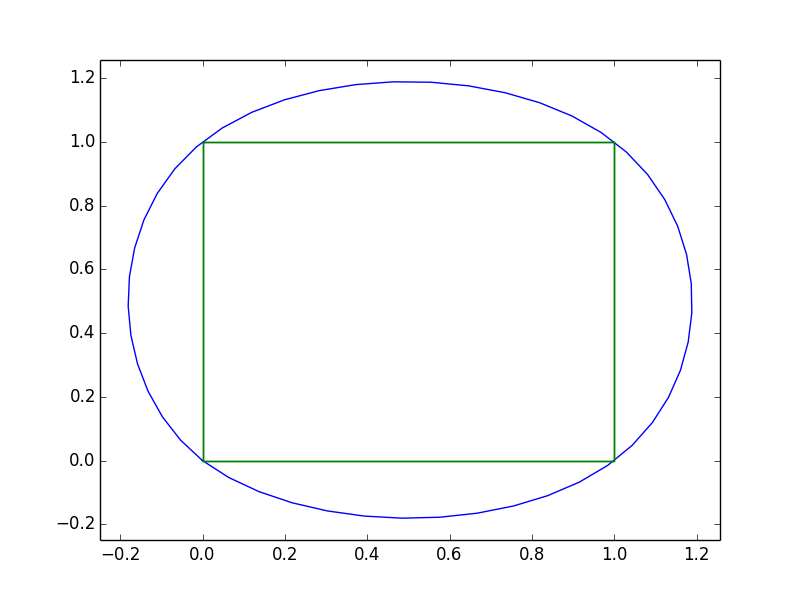
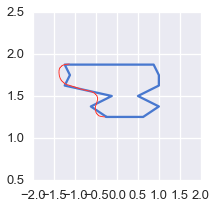
И просто чтобы показать, как это выглядит с вашими данными:

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d

x = [-0.25, -0.625, -0.125, -1.25, -1.125, -1.25,
     0.875, 1.0, 1.0, 0.5, 1.0, 0.625, -0.25]
y = [1.25, 1.375, 1.5, 1.625, 1.75, 1.875, 1.875,
     1.75, 1.625, 1.5, 1.375, 1.25, 1.25]

# Pad the x and y series so it "wraps around".
# Note that if x and y are numpy arrays, you'll need to
# use np.r_ or np.concatenate instead of addition!
orig_len = len(x)
x = x[-3:-1] + x + x[1:3]
y = y[-3:-1] + y + y[1:3]

t = np.arange(len(x))
ti = np.linspace(2, orig_len + 1, 10 * orig_len)

xi = interp1d(t, x, kind='cubic')(ti)
yi = interp1d(t, y, kind='cubic')(ti)

fig, ax = plt.subplots()
ax.plot(xi, yi)
ax.plot(x, y)
ax.margins(0.05)
plt.show()

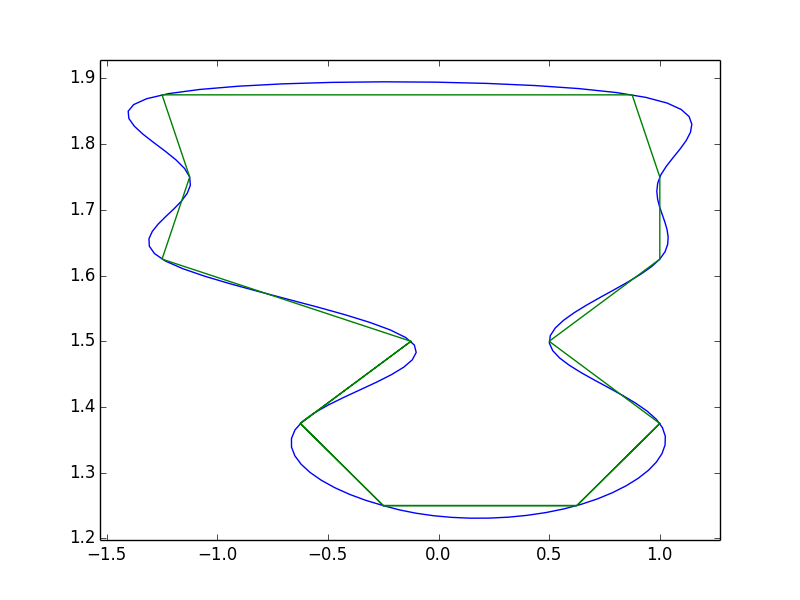
Обратите внимание, что с этим методом вы получаете немного "перерегулирования". Это связано с кубической сплайн-интерполяцией. Предложение @ pythonstarter - еще один хороший способ справиться с этим, но кривые Безье будут страдать от той же проблемы (математически они в основном эквивалентны, это просто вопрос определения контрольных точек). Существует ряд других способов обработки сглаживания, включая методы, специализированные для сглаживания многоугольника (например, полиномиальная аппроксимация с экспоненциальным ядром (PAEK)). Я никогда не пытался внедрить PAEK, поэтому я не уверен, насколько это важно. Если вам нужно сделать это более надежно, вы можете попробовать поискать PAEK или другой подобный метод.

Answer 3

Это скорее комментарий, чем ответ, но, возможно, вы можете попытаться определить этот многоугольник как кривую Безье. Код довольно прост, и я уверен, что вы знакомы с тем, как работают эти кривые. В этом случае эта кривая будет контрольным многоугольником. Но не все идеально: во-первых, это не действительно "сглаженная версия" этого многоугольника, а кривая и другое; чем выше степень кривой, тем меньше она выглядит как контрольный многоугольник. Я хочу сказать, что, возможно, вам следует попытаться решить эту проблему с помощью математических инструментов, а не пытаться сгладить, а не сгладить многоугольник с помощью навыков программирования.