Сколько хеш-функций требуется в алгоритме minhash

Question

Я стремлюсь реализовать minhashing, чтобы найти почти дублированный контент. http://blog.cluster-text.com/tag/minhash/ есть хорошее описание, но возникает вопрос о том, сколько алгоритмов хеширования вам нужно запустить по элементам документа в документе, чтобы получить приемлемые результаты.

В сообщении блога упоминалось что-то вроде 200 алгоритмов хеширования. http://blogs.msdn.com/b/spt/archive/2008/06/10/set-similarity-and-min-hash.aspx по умолчанию перечислено 100.

Очевидно, что с ростом числа хешей точность увеличивается, но сколько хеш-функций является разумным?

Цитировать из блога

Трудно получить полосу ошибок в нашей оценке сходства, намного меньшую, чем [7%], из-за того, как шкалы ошибок в статистически выбранных значениях масштабируются - чтобы сократить полосу ошибок пополам, нам потребуется в четыре раза больше выборок.

Означает ли это, что это означает, что уменьшение числа хэшей до 12 (200 / 4 / 4) приведет к частоте ошибок 28% (7 * 2 * 2)?

Answer 1

В значительной степени... но 28% будет "оценкой ошибки", означая, что сообщенные измерения часто будут неточными на +/- 28%.

Это означает, что измеренное значение 78% может легко быть получено только из 50% -ого сходства. Или что 50% -ое сходство может быть легко сообщено как 22%. Для меня это звучит недостаточно точно для деловых ожиданий.

Математически, если вы сообщаете две цифры, вторая должна быть значимой.

Почему вы хотите уменьшить количество хеш-функций до 12? Что на самом деле означает "200 хеш-функций", так это вычислить хеш-код приличного качества для каждого гальки / строки один раз, а затем примените 200 дешевых и быстрых преобразований, чтобы подчеркнуть определенные факторы / вывести определенные биты вперед.

Я рекомендую объединить побитовые вращения (или тасование) и операцию XOR. Каждая хеш-функция может объединять вращение на некоторое количество битов, а затем выполнять XOR с помощью случайно сгенерированного целого числа.

Это как "расширяет" избирательность функции min() по битам, так и относительно того, какое значение min() заканчивается выбором.

Основанием для поворота является то, что "min(Int)" будет 255 раз из 256 выбирать только в пределах 8 старших разрядов. Только если все старшие биты одинаковы, младшие биты оказывают какое-либо влияние на сравнение... поэтому расширение может быть полезным, чтобы избежать чрезмерного акцентирования только одного или двух символов в гальке.

Основанием для XOR является то, что само по себе побитовое вращение (ROTR) может в 50% случаев (когда 0 бит сдвинуты слева направо) сходиться к нулю, и это приведет к тому, что "отдельные" хеш-функции будут отображать нежелательные тенденция совпадать с нулем вместе - таким образом, чрезмерная тенденция для них в конечном итоге выбрать один и тот же, а не независимый.

Существует очень интересная "побитовая" причуда целых чисел со знаком, где MSB отрицателен, но все последующие биты положительны, что делает тенденцию вращения сходиться гораздо менее заметной для целых чисел со знаком - где это было бы очевидно для неподписанных. XOR все равно должен использоваться в этих условиях.

Java имеет встроенные 32-битные хэш-коды. А если вы используете библиотеки Google Guava, доступны 64-битные хеш-коды.

Спасибо @BillDimm за его вклад и настойчивость в указании, что XOR был необходим.

Answer 2

Один из способов генерирования 200 значений хеш-функции состоит в том, чтобы сгенерировать одно значение хеш-функции с использованием хорошего алгоритма хеширования и дешево сгенерировать 199 значений, XOR с помощью правильного значения хеш-функции с 199 наборами произвольно выглядящих битов, имеющих ту же длину, что и значение хорошего хеш-значения (т. Е. Если хороший хеш составляет 32 бита, создайте список из 199 32-битных псевдослучайных целых чисел и XOR каждого хорошего хеша с каждым из 199 случайных целых чисел).

Не просто вращайте биты, чтобы дешево генерировать хеш-значения, если вы используете целые числа без знака (целые числа со знаком - это хорошо), - которые часто выбирают один и тот же шингл снова и снова. Поворот битов на единицу - это то же самое, что деление на 2 и копирование старого младшего бита в новое местоположение старшего бита. Примерно 50% хороших значений хеш-функции будут иметь 1 в младшем бите, поэтому они будут иметь огромные значения хэш-функции без молитвы о том, чтобы быть минимальным хэшем, когда этот младший бит вращается в месте старшего бита. Остальные 50% хороших хеш-значений будут просто равны их исходным значениям, разделенным на 2, когда вы сдвигаетесь на один бит. Деление на 2 не меняет, какое значение является наименьшим. Таким образом, если бит, который дал минимальный хэш с хорошей хэш-функцией, имеет нулевой бит (вероятность 50% этого), он снова даст минимальное хеш-значение, когда вы сдвигаетесь на один бит. В качестве крайнего примера, если бит с наименьшим значением хеш-функции из хорошей хэш-функции имеет значение хеш-функции 0, он всегда будет иметь минимальное значение хеш-значения, независимо от того, насколько вы вращаете биты. Эта проблема не возникает с целыми числами со знаком, поскольку минимальные значения хеш-функции имеют крайние отрицательные значения, поэтому они, как правило, имеют 1 в старшем бите, за которым следуют нули (100...). Таким образом, только значения хеш-функции с младшим битом, равным 1, будут иметь шанс стать новым самым низким значением хэш-функции после уменьшения на один бит. Если бит с минимальным значением хеш-функции имеет 1 в младшем бите, после поворота на один бит он будет выглядеть как 1100..., так что почти наверняка он будет выбит другим битом, который имеет значение, подобное 10... после поворота, и проблема того, что один и тот же гонт выбирается дважды подряд с вероятностью 50%, исключается.

Answer 3

То, что вы хотите, может быть легко получено из универсального хеширования. Популярные учебники, такие как Corman и др., Очень читаемы в разделе 11.3.3, с. 265-268. Короче говоря, вы можете генерировать семейство хеш-функций, используя следующее простое уравнение:

h(x,a,b) = ((ax+b) mod p) mod m

• х ключ, который вы хотите хэшировать
• a - любое нечётное число, которое вы можете выбрать от 1 до p-1 включительно.
• b - любое число, которое вы можете выбрать от 0 до p-1 включительно.
• р простое число, которое больше максимально возможного значения х
• m - максимально возможное значение, которое вы хотите для хэш-кода + 1

Выбирая различные значения a и b, вы можете генерировать множество хеш-кодов, которые не зависят друг от друга.

Оптимизированная версия этой формулы может быть реализована следующим образом в C/C++/C#/Java:

(unsigned) (a*x+b) >> (w-M)

Здесь - w - размер машинного слова (обычно 32) - M - размер хеш-кода, который вы хотите в битах - a - любое нечетное целое число, которое подходит к машинному слову - b - любое целое число меньше 2^(wM)

Выше работает для хеширования числа. Чтобы хэшировать строку, получите хеш-код, который вы можете получить с помощью встроенных функций, таких как GetHashCode, а затем используйте это значение в приведенной выше формуле.

Например, предположим, что вам нужно 200 16-битного хеш-кода для строки s, тогда следующий код может быть записан как реализация:

public int[] GetHashCodes(string s, int count, int seed = 0)
{
    var hashCodes = new int[count];
    var machineWordSize = sizeof(int);
    var hashCodeSize = machineWordSize / 2; 
    var hashCodeSizeDiff = machineWordSize - hashCodeSize;
    var hstart = s.GetHashCode();
    var bmax = 1 << hashCodeSizeDiff;
    var rnd = new Random(seed);     

    for(var i=0; i < count; i++) 
    {
        hashCodes[i] = ((hstart * (i*2 + 1)) + rnd.Next(0, bmax)) >>  hashCodeSizeDiff;
    }
}

Заметки:

1. Я использую размер хеш-кода как половину машинного слова, которое в большинстве случаев будет 16-битным. Это не идеально и имеет гораздо больше шансов на столкновение. Это можно использовать, обновив всю арифметику до 64-битной.
2. Обычно вы хотите выбрать a и b оба случайно в указанных выше диапазонах.

Answer 4

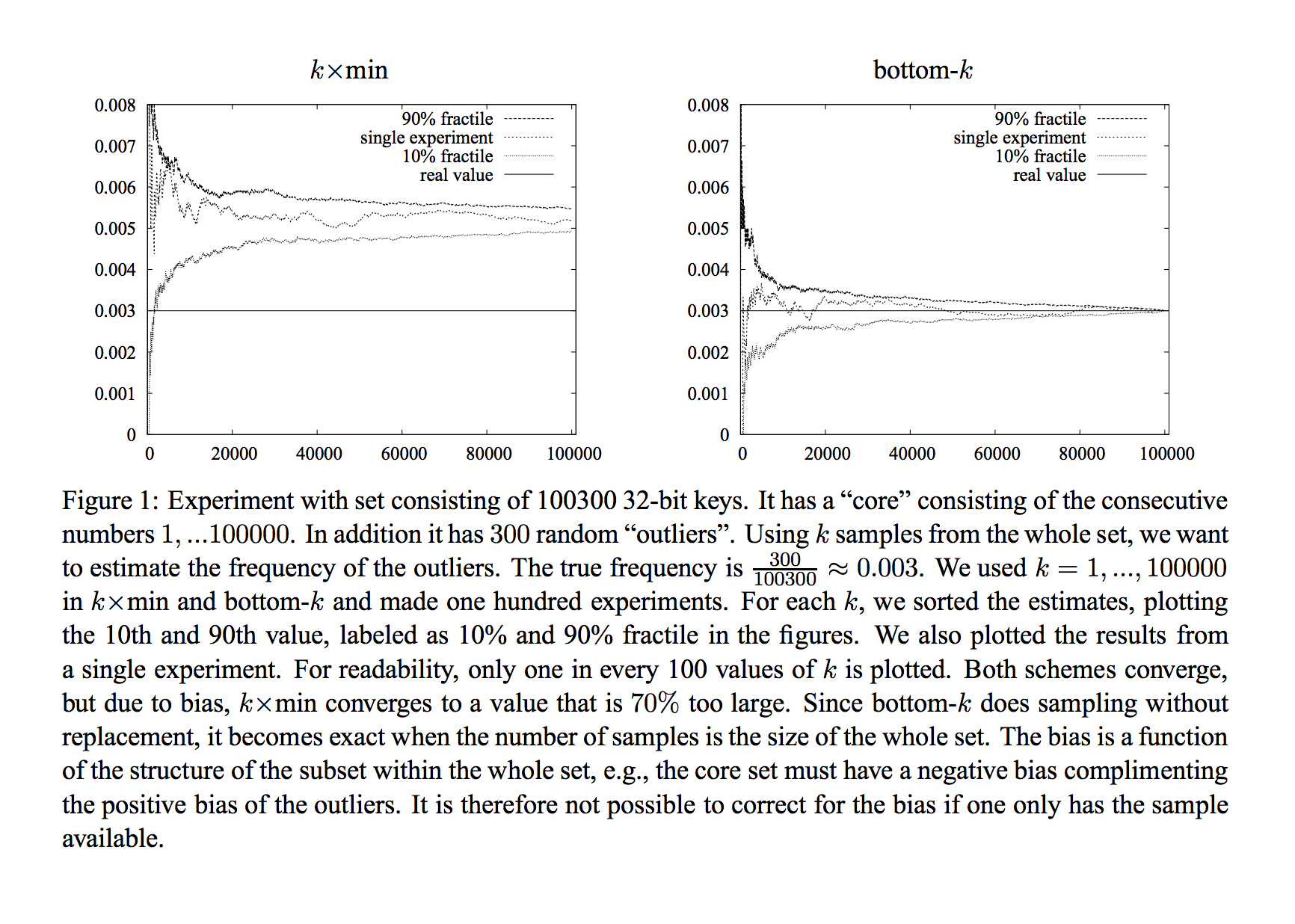
Проверьте эту статью для современных практических и теоретических границ. У этого есть хороший график (ниже), объясняющий, почему вы, вероятно, хотите использовать только одну 2-независимую хеш-функцию и сохранить k наименьшие значения.

При оценке размеров набора на бумаге показано, что вы можете получить относительную ошибку приблизительно ε = 1/sqrt(f k) где f это сходство Жаккарда и k количество сохраненных значений Так что, если вы хотите ошибку ε, тебе нужно k=1/(fε^2) или если ваши наборы имеют сходство вокруг 1/3 и ты хочешь 10% Относительная ошибка, вы должны сохранить 300 наименьшие значения.

Answer 5

Кажется, что другой способ получить N чисел хороших хэшированных значений состоит в том, чтобы засолить один и тот же хеш с N различными солт-значениями.

На практике, если применить солт второй, кажется, что вы могли бы хэшировать данные, а затем "клонировать" внутреннее состояние вашего хеша, добавить первую соль и получить ваше первое значение. Вы вернете этот клон в чистое клонированное состояние, добавите вторую соль и получите второе значение. Промыть и повторить для всех N предметов.

Вероятно, не так дешево, как XOR в зависимости от значений N, но кажется, что есть возможность для получения более качественных результатов при минимальных дополнительных затратах, особенно если хешируемые данные намного больше, чем солт-значение.