Проблема в расчете ошибки для нескольких прогонов эксперимента

Question

В следующем коротком примере кода, который является частью большего кода, я пытаюсь найти среднеквадратическую ошибку, которая является метрикой производительности, которая будет определять, насколько хорошо функция была оценена путем изучения MSE. Чем ниже значение MSE, тем ближе оцениваемый результат к истинному результату. Я повторяю эксперимент 10 раз с 10 различными наборами данных и записываю минимальную ошибку среди всех наборов данных. Весь этот процесс выполняется 100 раз. Данные представляют собой матрицу размером 10*3, т.е. 10 выборок данных, каждая из которых содержит 3 элемента.

У меня есть сомнения в том, как рассчитать среднеквадратичную ошибку, среднеквадратичную ошибку и минимальную ошибку. В конце мне интересно построить график, который показывает убывающую кривую ошибки, где ось X = количество оценок функции и ось Y = MinimumErr, чтобы показать функцию ошибки, уменьшающуюся несколько раз за 100 попыток программы. Пожалуйста помоги

for trials = 1:100
    for expt = 1:10
        DataSet = Data(expt,:);
        for evaluation = 1:50
            %Evaluate a function 
            [B1 B2 B3] = F(DataSet)

            %Find error between the desired outputs(A1,A2,A3) of the function and the obtained output (B1,B2,B3). The function evaluation returns these 3 values.
            err(evaluation,:) = (A1-B1)^2+ (A2-B2)^2 + (A3-B3)^2;
        end
        MeanSqErr = sum(err)/(3*evaluation);
    end
    MinimumErr(expt)  = min(err);
end
AverageMSE= sum(MeanSqErr)/(trials)

Answer 1

Прежде чем написать хотя бы одну строчку кода, необходимо понять, чего мы хотим.

Средняя квадратическая ошибка (MSE) - это измерение разности, определяемой как:

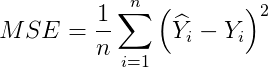
где Yhat - расчетный результат, а Y - эталонный выход. Оба сигнала / вектора имеют одинаковое количество точек, равное n.

Затем вы хотите усредненную MSE за m экспериментов, следовательно, вам нужно применить оператор среднего.

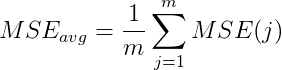
Например, у вас есть эталонное измерение Y = [0 1 3 6 10], В первом эксперименте вы измеряете Y1 = [1 2 4 5 9]и во втором эксперименте вы измеряете Y2 = [0 1 2 3 8], MSE первого и второго эксперимента равны 1 и 2,8 соответственно. Следовательно, среднее значение MSE по всем экспериментам составляет 1,9.

Y  = [0 1 3 6 10];
Y1 = [1 2 4 5 9];
Y2 = [0 1 2 3 8];

MSE1 = ((Y-Y1)*(Y-Y1).')/numel(Y);
MSE2 = ((Y-Y2)*(Y-Y2).')/numel(Y);
MSEavg = (MSE1+MSE2)/2; 

---

Ваш код кажется правильным, но грязным, за исключением MinimumErr переменная, которая должна быть внутри цикла for expt = 1:10, Я бы немного реорганизовал ваш код:

% Parameters
Ntrials = 100;
Nexpt   = 10;
Neval   = 50;

% Calculate
A = [A1 A2 A3];
MSE = zeros(Ntrials,Nexpt,Neval);
for trials = 1:Ntrials
    for expt = 1:Nexpt
        for eval = 1:Neval
            % Evaluate a function 
            [B1,B2,B3] = F(Data(expt,:));
            B = [B1 B2 B3];
            % Find MSE 
            MSE(trials,expt,eval) = ((A-B)*(A-B).')/numel(A);
        end
    end
end

% Statistics
MeanSqErr  = mean(MSE,3);
MinimumErr = min(MeanSqErr,[],2);
AverageMSE = mean(MeanSqErr,2);

% Plot
figure; plot(1:Ntrials,AverageMSE); xlabel('#trials'); ylabel('MSE');