Отсутствует несколько путей в алгоритме Эдмондса Карпа Макса

Question

Я бы реализовал алгоритм Эдмонда Карпа, но, похоже, он не правильный, и я не получаю правильный поток, рассмотрим следующий график и поток от 4 до 8:

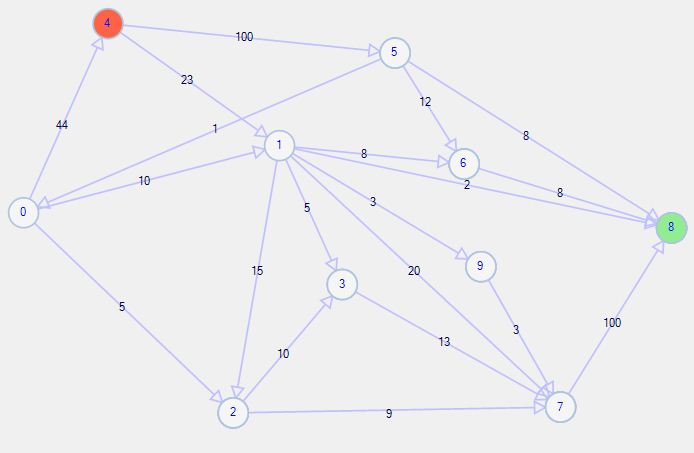
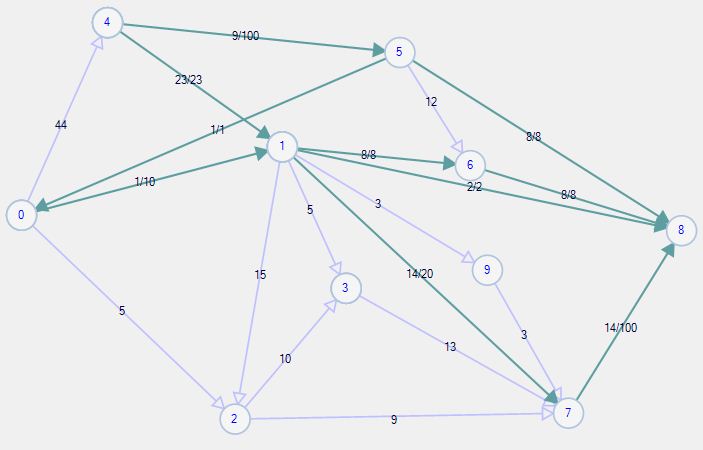
Алгоритм работает следующим образом:

Сначала находит 4→1→8, затем находит 4→5→8 после этого 4→1→6→8

И я думаю, что третий путь неправильный, потому что, используя этот путь, мы не можем использовать поток из 6→8 (потому что он использовал), и на самом деле мы не можем использовать поток из 4→5→6→8.

Фактически, если мы выберем 4→5→6→8, а затем 4→1→3→7→8, а затем 4→1→3→7→8, мы можем получить лучший поток (40).

Я реализовал алгоритм из примера кода вики. Я думаю, что мы не можем использовать какой-либо действительный путь, и на самом деле этот жадный выбор неверен.

Я ошибся?

Код такой, как показано ниже (в C# порог равен 0 и не влияет на алгоритм):

   public decimal EdmondKarps(decimal[][] capacities/*Capacity matrix*/,
                    List<int>[] neighbors/*Neighbour lists*/,
                    int s /*source*/,
                    int t/*sink*/,
                    decimal threshold,
                    out decimal[][] flowMatrix
                    /*flowMatrix (A matrix giving a legal flowMatrix with the maximum value)*/
                    )
    {
        THRESHOLD = threshold;
        int n = capacities.Length;
        decimal flow = 0m; // (Initial flowMatrix is zero)
        flowMatrix = new decimal[n][]; //array(1..n, 1..n) (Residual capacity from u to v is capacities[u,v] - flowMatrix[u,v])
        for (int i = 0; i < n; i++)
        {
            flowMatrix[i] = new decimal[n];
        }

        while (true)
        {
            var path = new int[n];
            var pathCapacity = BreadthFirstSearch(capacities, neighbors, s, t, flowMatrix, out path);
            if (pathCapacity <= threshold)
                break;
            flow += pathCapacity;

            //(Backtrack search, and update flowMatrix)
            var v = t;
            while (v != s)
            {
                var u = path[v];
                flowMatrix[u][v] = flowMatrix[u][v] + pathCapacity;
                flowMatrix[v][u] = flowMatrix[v][u] - pathCapacity;
                v = u;
            }
        }
        return flow;
    }

    private decimal BreadthFirstSearch(decimal[][] capacities, List<int>[] neighbors, int s, int t, decimal[][] flowMatrix, out int[] path)
    {
        var n = capacities.Length;
        path = Enumerable.Range(0, n).Select(x => -1).ToArray();//array(1..n)
        path[s] = -2;
        var pathFlow = new decimal[n];
        pathFlow[s] = Decimal.MaxValue; // INFINT
        var Q = new Queue<int>(); // Q is exactly Queue :)
        Q.Enqueue(s);
        while (Q.Count > 0)
        {
            var u = Q.Dequeue();
            for (int i = 0; i < neighbors[u].Count; i++)
            {
                var v = neighbors[u][i];
                //(If there is available capacity, and v is not seen before in search)
                if (capacities[u][v] - flowMatrix[u][v] > THRESHOLD && path[v] == -1)
                {
                    // save path:
                    path[v] = u;
                    pathFlow[v] = Math.Min(pathFlow[u], capacities[u][v] - flowMatrix[u][v]);
                    if (v != t)
                        Q.Enqueue(v);
                    else
                        return pathFlow[t];
                }
            }
        }
        return 0;
    }

Answer 1

Способ выбора путей не важен.

Вы должны добавить ребра пути в обратном порядке с пропускной способностью пути и уменьшить вместимость ребер пути на это значение.

На самом деле это решение работает:

while there is a path with positive capacity from source to sink{
    find any path with positive capacity from source to sink, named P with capacity C.
    add C to maximum_flow_value.
    reduce C from capacity of edges of P.
    add C to capacity of edges of reverse_P.
}

Наконец, значение максимального потока является суммой Cв петле.

Если вы хотите видеть поток в ребрах в максимальном потоке, который вы создали, вы можете где-то сохранить исходный граф, поток в ребре e будет иметь вид original_capacity_e - current_capacity_e.