Numpy восемь функций с правильными знаками

Question

Я хотел бы рассчитать собственные векторы матрицы второй производной в Python. Согласно математике первый вектор должен быть равен sin-функции между 0 и pi, второй равен sin-функции между 0 и 2*pi. Таким образом мой код выглядит

import numpy as np
from matplotlib import pyplot as plt
from scipy import sparse
import scipy.integrate as integrate
import scipy.special as special
import scipy

def create_second_deriv(size, h):
    delta_matrix_2_second_diff = (np.eye(size, dtype=np.float)*-2+np.eye(size, k=-1,dtype=np.float)*1+np.eye(size, k=1,dtype=np.float)*1)
    delta_matrix_2_second_diff /= (h*h)
    return -1*delta_matrix_2_second_diff

delta_x = 0.001
x = np.linspace(0, 1, (int)(1/delta_x))
delta_matrix = create_second_deriv(len(x), delta_x)
w, v = scipy.linalg.eigh(delta_matrix)

plt.plot(v.tolist()[0])
plt.show()
plt.plot(v.tolist()[1])
plt.show()

Теперь, что я получаю в качестве вывода, это 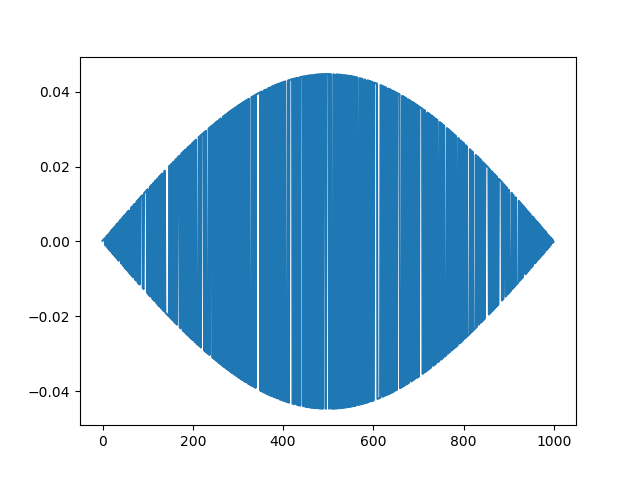как сюжет для первого собственного вектора, и 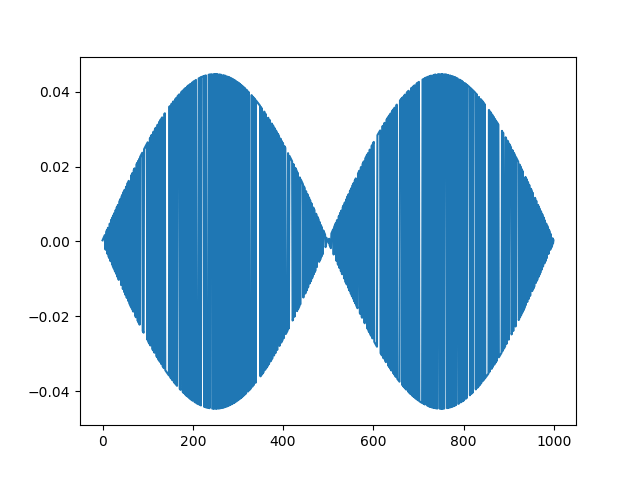как сюжет для второго собственного вектора. Я уже знаю, что знаки для различных значений являются произвольными, но в моем случае они важны для дальнейшей обработки. Есть ли способ "перевернуть" знаки так, чтобы результирующие значения были примерно равны ожидаемым функциям? Просто используя abs()-функция не поможет в этом случае.

Answer 1

Есть гоча с scipy.linalg.eigh() функция:

Будьте очень осторожны, используя eigh() рутина, чтобы получить собственные значения, хотя. В ней похоронена "гоча".

Синтаксис:

(eigenvalues, eigenvectors) = eigh(matrix)

Это возвращает массив собственных значений и двумерный массив собственных векторов (каждый собственный вектор состоит из множества компонентов).

И есть гоча. Допустим, вы хотите nСобственное значение и собственный вектор. Я бы написал:

eigenvalues[n]
eigenvectors[n]

И я был бы ужасно неправ. Собственные векторы и собственные значения имеют общий индекс, но индекс для собственного вектора - это второй столбец:

eigenvectors[:,n]

Таким образом, последние четыре строки вашего кода должны быть изменены на:

plt.plot(v[:,0])
plt.show()
plt.plot(v[:,1])
plt.show()