Получить подграф кратчайшего пути между n узлами

Question

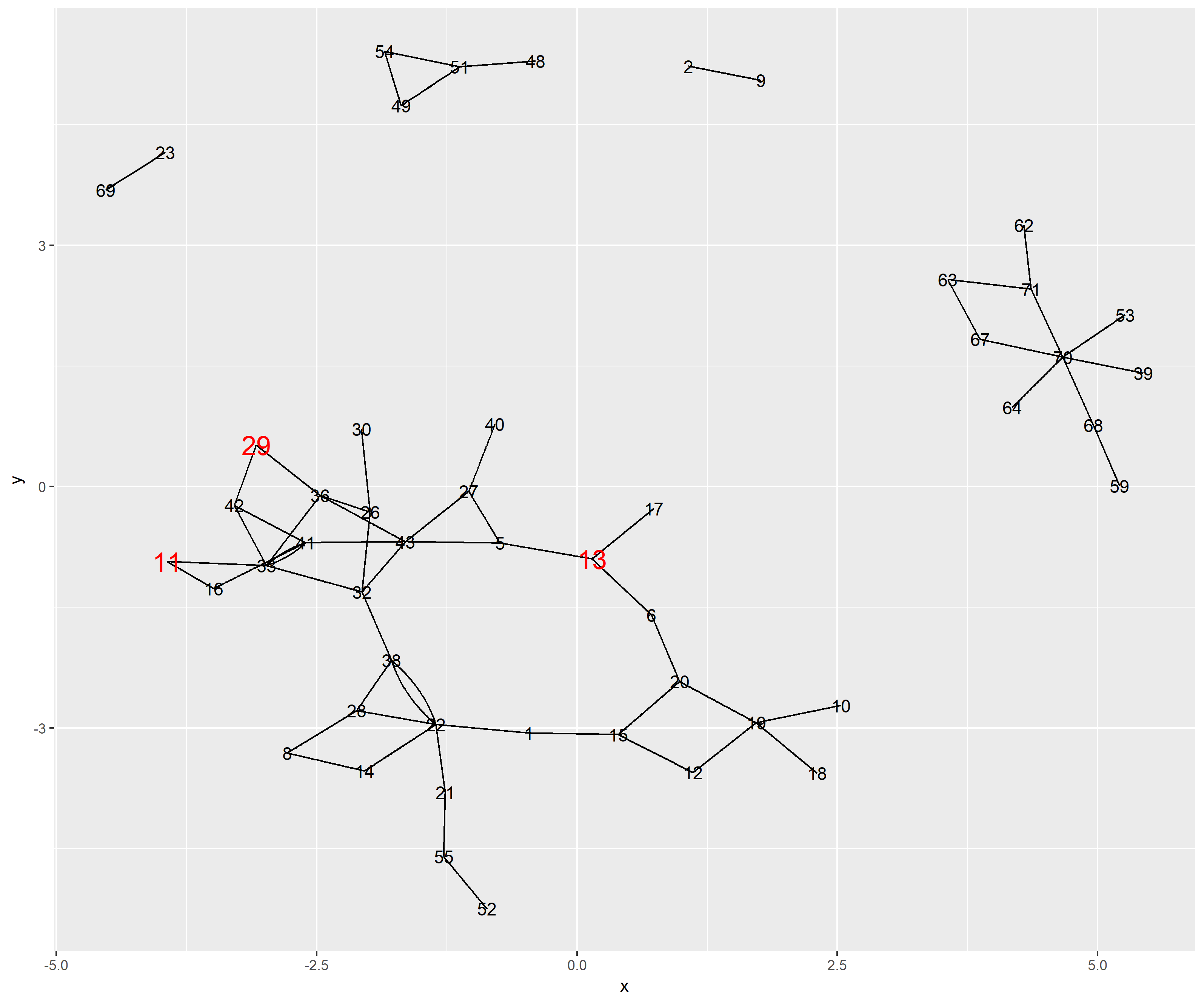
У меня есть невзвешенный граф, и я хочу получить подграф, который имеет только узлы и ребра, которые содержат кратчайшие пути между n известными узлами. В этом случае 3 узла (11, 29 и 13 являются именами).

Вопрос

Как я могу получить подграф кратчайшего пути между n узлами в R?

MWE

library(ggraph)
library(igraph)

hs <- highschool[highschool$year == '1958',]
set.seed(11)
graph <- graph_from_data_frame(hs[sample.int(nrow(hs), 60),])


# plot using ggraph
ggraph(graph, layout = 'kk') + 
    geom_edge_fan() + 
    geom_node_text(aes(label = name)) 

Желаемый вывод

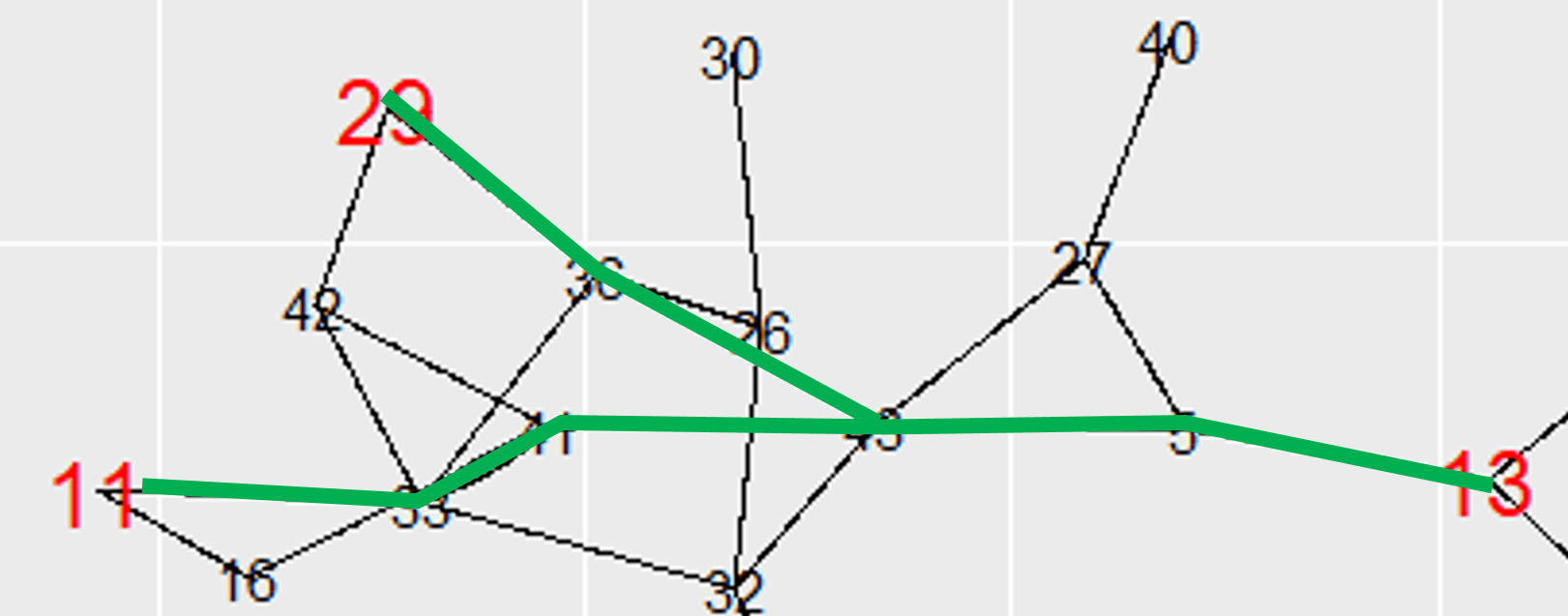
Желаемым результатом будет следующий зеленый подграф (или близко, я смотрю на график выше и визуально выбираю, что будет подграфом), игнорируя / удаляя другие узлы и ребра.

Answer 1

Вы не можете найти кратчайший путь между n узлами. Поскольку кратчайший путь определяется только между двумя узлами.

Я думаю, что вы хотите кратчайший путь от 1 узел к другому n-1 узел, который вы можете использовать
get_all_shortest_paths(v, to=None, mode=ALL) от igraph библиотека.

• v - источник для рассчитанных путей
• to - селектор вершин, описывающий пункт назначения для вычисленных путей. Это может быть один идентификатор вершины, список идентификаторов вершин, одно имя вершины, список имен вершин. Ни один не означает все вершины.
• Режим - направленность путей. IN означает рассчитать входящие пути, OUT означает рассчитать исходящие пути, ALL означает рассчитать оба.

Возвращает: весь кратчайший путь от данного узла ко всем другим достижимым узлам в графе в списке.
get_all_shortest_paths

Итак, теперь вам нужно создать график из списка кратчайших путей.

1. Инициализируйте пустой график, затем добавьте к нему весь путь из списка путей.
   добавление пути в граф

   ИЛИ ЖЕ

2. сделать график для каждого найденного кратчайшего пути и взять объединение графов.
   Юнион Играф

Answer 2

Вам нужна матрица кратчайших путей, чтобы затем создать подграф, используя объединение всех ребер, принадлежащих этим путям.

Пусть ключевые вершины будут теми вершинами, между которыми появляется нужный вам подграф. Вы говорите, что у вас есть три таких ключевых вершины.

Учтите, что кратчайший путь между любыми i а также j из них unlist(shortest_paths(g, i, j, mode="all", weights=NULL)$vpath), Вы хотели бы перечислить все комбинации ij (1-2, 1-3, 2-3 в вашем случае) ваших ключевых вершин, а затем перечислить все вершины, которые появляются на путях между ними. Когда-нибудь, конечно же, одни и те же вершины появляются на кратчайших путях более чем одной из ваших ij-пар (см. Центральность промежуточности). Ваш желаемый подграф должен включать только эти вершины, которые вы можете дать induced_subgraph(),

Тогда возникает еще одна интересная проблема. Не все ребра между выбранными вами вершинами являются частью ваших кратчайших путей. Я не уверен в том, что вы хотите в своем подграфе, но я предполагаю, что вам нужны только вершины и ребра, являющиеся частью кратчайших путей. Руководство по induced_subgraph() Говорит, что eids может быть предоставлен для фильтрации подграфов по краям, но я не получил это работать. Комментарии на это приветствуются, если кто-нибудь взломает его. Чтобы создать подграф только с теми ребрами и вершинами, которые действительно находятся на вашем кратчайшем пути, некоторые лишние ребра должны быть удалены.

Ниже приведен пример, когда некоторые ключевые вершины выбираются случайным образом, визуализируется проблема с избыточным краем подграфа и генерируется правильный подграф только с более короткими путями:

library(igraph)
N <- 40 # Number of vertices in a random network
E <- 70 # Number of edges in a random network
K <- 5  # Number of KEY vertices between which we are to calculate the
        # shortest paths and extract a sub-graph.

# Make a random network
g <- erdos.renyi.game(N, E, type="gnm", directed = FALSE, loops = FALSE)
V(g)$label <- NA
V(g)$color <- "white"
V(g)$size <- 8
E(g)$color <- "gray"

# Choose some random verteces and mark them as KEY vertices
key_vertices <- sample(1:N, 5)
g <- g %>% set_vertex_attr("color", index=key_vertices, value="red")
g <- g %>% set_vertex_attr("size", index=key_vertices, value=12)

# Find shortest paths between two vertices in vector x:
get_path <- function(x){
  # Get atomic vector of two key verteces and return their shortest path as vector.
  i <- x[1]; j <- x[2]
  # Check distance to see if any verticy is outside component. No possible
  # connection will return infinate distance:
  if(distances(g,i,j) == Inf){
    path <- c()
  } else {
    path <- unlist(shortest_paths(g, i, j, mode="all", weights=NULL)$vpath)
  }
}

# List pairs of key vertices between which we need the shortest path
key_el <- expand.grid(key_vertices, key_vertices)
key_el <- key_el[key_el$Var1 != key_el$Var2,]

# Get all shortest paths between each pair of key_vertices:
paths <- apply(key_el, 1, get_path)

# These are the vertices BETWEEN key vertices - ON the shortest paths between them:
path_vertices <- setdiff(unique(unlist(paths)), key_vertices)
g <- g %>% set_vertex_attr("color", index=path_vertices, value="gray")


# Mark all edges of a shortest path
mark_edges <- function(path, edges=c()){
  # Get a vector of id:s of connected vertices, find edge-id:s of all edges between them.
  for(n in 1:(length(path)-1)){
    i <- path[n]
    j <- path[1+n]
    edge <- get.edge.ids(g, c(i,j), directed = TRUE, error=FALSE, multi=FALSE)
    edges <- c(edges, edge)
  }
  # Return all edges in this path
  (edges)
}

# Find all edges that are part of the shortest paths between key vertices
key_edges <- lapply(paths, function(x) if(length(x) > 1){mark_edges(x)})
key_edges <- unique(unlist(key_edges))
g <- g %>% set_edge_attr("color", index=key_edges, value="green")

# This now shoes the full graph and the sub-graph which will be created
plot(g)

# Create sub-graph:
sg_vertices <- sort(union(key_vertices, path_vertices))
unclean_sg <- induced_subgraph(g, sg_vertices)
# Note that it is essential to provide both a verticy AND an edge-index for the
# subgraph since edges between included vertices do not have to be part of the
# calculated shortest path. I never used it before, but eids=key_edges given
# to induced_subgraph() should work (even though it didn't for me just now).

# See the problem here:
plot(unclean_sg)

# Kill edges of the sub-graph that were not part of shortest paths of the mother
# graph:
sg <- delete.edges(unclean_sg, which(E(unclean_sg)$color=="gray"))

# Plot a comparison:
l <-layout.auto(g)
layout(matrix(c(1,1,2,3), 2, 2, byrow = TRUE))
plot(g, layout=l)
plot(unclean_sg, layout=l[sg_vertices,])  # cut l to keep same layout in subgraph
plot(sg, layout=l[sg_vertices,])          # cut l to keep same layout in subgraph