Как скрыть линию за графиком поверхности в matplotlib?

Question

Я хочу нанести данные с помощью Matplotlib с помощью карты цветов на поверхности сферы. Кроме того, я хотел бы добавить линейный 3D-график. Код, который у меня пока есть, такой:

import matplotlib
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np


NPoints_Phi         = 30
NPoints_Theta       = 30

radius              = 1
pi                  = np.pi
cos                 = np.cos
sin                 = np.sin

phi_array           = ((np.linspace(0, 1, NPoints_Phi))**1) * 2*pi
theta_array         = (np.linspace(0, 1, NPoints_Theta) **1) * pi


phi, theta          = np.meshgrid(phi_array, theta_array) 


x_coord             = radius*sin(theta)*cos(phi)
y_coord             = radius*sin(theta)*sin(phi)
z_coord             = radius*cos(theta)


#Make colormap the fourth dimension
color_dimension     = x_coord 
minn, maxx          = color_dimension.min(), color_dimension.max()
norm                = matplotlib.colors.Normalize(minn, maxx)
m                   = plt.cm.ScalarMappable(norm=norm, cmap='jet')
m.set_array([])
fcolors             = m.to_rgba(color_dimension)



theta2              = np.linspace(-np.pi,  0, 1000)
phi2                = np.linspace( 0 ,  5 * 2*np.pi , 1000)


x_coord_2           = radius * np.sin(theta2) * np.cos(phi2)
y_coord_2           = radius * np.sin(theta2) * np.sin(phi2)
z_coord_2           = radius * np.cos(theta2)

# plot
fig                 = plt.figure()

ax                  = fig.gca(projection='3d')
ax.plot(x_coord_2, y_coord_2, z_coord_2,'k|-', linewidth=1 )
ax.plot_surface(x_coord,y_coord,z_coord, rstride=1, cstride=1, facecolors=fcolors, vmin=minn, vmax=maxx, shade=False)
fig.show()

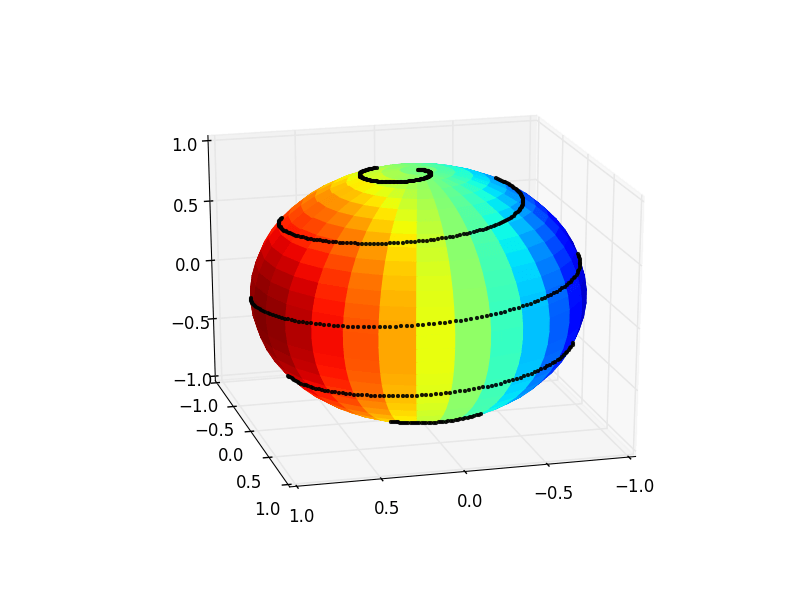
Этот код создает изображение, которое выглядит так: 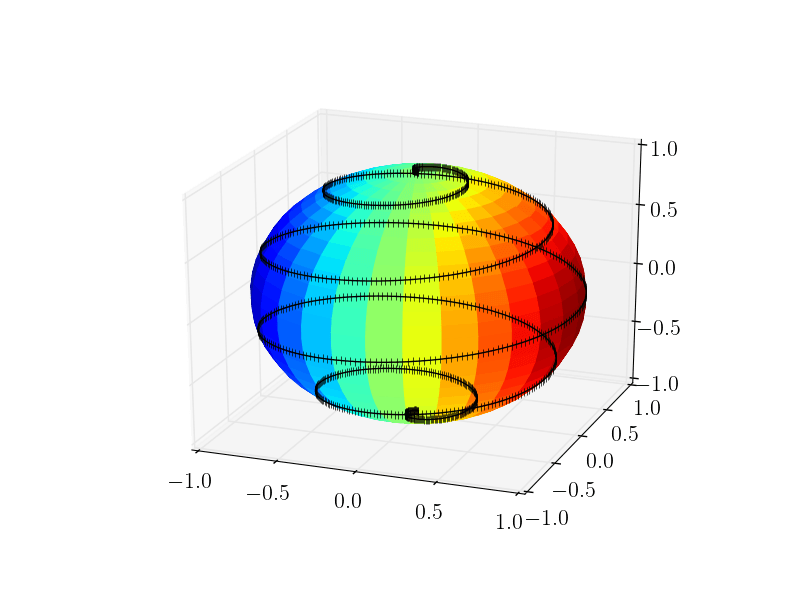что почти то, что я хочу. Однако черная линия должна быть скрыта графиком поверхности, когда он находится на заднем плане, и видимой, когда он находится на переднем плане. Другими словами, черная линия не должна "просвечивать" сферу.

Можно ли это сделать в Matplotlib и без использования Mayavi?

Answer 1

Проблема в том, что matplotlib не является трассировщиком лучей и на самом деле не предназначен для работы с 3D-графикой. Как таковой, он работает с системой слоев в 2D-пространстве, и объекты могут находиться в слое, более спереди или больше сзади. Это можно установить с помощью zorder Ключевой аргумент для большинства функций построения. Однако в matplotlib отсутствует информация о том, находится ли объект впереди или позади другого объекта в трехмерном пространстве. Поэтому вы можете иметь полную линию видимой (перед сферой) или скрытой (за ней).

Решением было бы рассчитать точки, которые должны быть видны сами. Я говорю о точках здесь, потому что линия будет соединять видимые точки "через" сферу, что нежелательно. Поэтому я ограничиваю себя построением точек - но если их у вас достаточно, они выглядят как линия:-).

Вычисление точек, которые должны быть видны, не является слишком сложным для идеальной сферы, и идея заключается в следующем:

1. Получить угол обзора 3D-графика
2. Исходя из этого, рассчитать вектор нормали к плоскости зрения в координатах данных в направлении обзора.
3. Вычислить скалярное произведение между этим вектором нормалей (называемый X в приведенном ниже коде) и линия указывает, чтобы использовать этот скалярный продукт как условие того, показывать ли точки или нет. Если скалярное произведение меньше 0 тогда соответствующая точка находится на другой стороне плоскости наблюдения, если смотреть со стороны наблюдателя, и поэтому ее показывать не следует.
4. Отфильтруйте точки по условию.

Еще одна дополнительная задача состоит в том, чтобы затем адаптировать показанные точки для случая, когда пользователь поворачивает вид. Это достигается путем подключения motion_notify_event к функции, которая обновляет данные, используя процедуру сверху, на основе вновь установленного угла обзора.

Посмотрите код ниже о том, как это реализовать.

import matplotlib
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np


NPoints_Phi         = 30
NPoints_Theta       = 30

phi_array           = ((np.linspace(0, 1, NPoints_Phi))**1) * 2*np.pi
theta_array         = (np.linspace(0, 1, NPoints_Theta) **1) * np.pi

radius=1
phi, theta          = np.meshgrid(phi_array, theta_array) 

x_coord             = radius*np.sin(theta)*np.cos(phi)
y_coord             = radius*np.sin(theta)*np.sin(phi)
z_coord             = radius*np.cos(theta)

#Make colormap the fourth dimension
color_dimension     = x_coord 
minn, maxx          = color_dimension.min(), color_dimension.max()
norm                = matplotlib.colors.Normalize(minn, maxx)
m                   = plt.cm.ScalarMappable(norm=norm, cmap='jet')
m.set_array([])
fcolors             = m.to_rgba(color_dimension)

theta2              = np.linspace(-np.pi,  0, 1000)
phi2                = np.linspace( 0, 5 * 2*np.pi , 1000)

x_coord_2           = radius * np.sin(theta2) * np.cos(phi2)
y_coord_2           = radius * np.sin(theta2) * np.sin(phi2)
z_coord_2           = radius * np.cos(theta2)

# plot
fig = plt.figure()

ax = fig.gca(projection='3d')
# plot empty plot, with points (without a line)
points, = ax.plot([],[],[],'k.', markersize=5, alpha=0.9)
#set initial viewing angles
azimuth, elev = 75, 21
ax.view_init(elev, azimuth )

def plot_visible(azimuth, elev):
    #transform viewing angle to normal vector in data coordinates
    a = azimuth*np.pi/180. -np.pi
    e = elev*np.pi/180. - np.pi/2.
    X = [ np.sin(e) * np.cos(a),np.sin(e) * np.sin(a),np.cos(e)]  
    # concatenate coordinates
    Z = np.c_[x_coord_2, y_coord_2, z_coord_2]
    # calculate dot product 
    # the points where this is positive are to be shown
    cond = (np.dot(Z,X) >= 0)
    # filter points by the above condition
    x_c = x_coord_2[cond]
    y_c = y_coord_2[cond]
    z_c = z_coord_2[cond]
    # set the new data points
    points.set_data(x_c, y_c)
    points.set_3d_properties(z_c, zdir="z")
    fig.canvas.draw_idle()

plot_visible(azimuth, elev)
ax.plot_surface(x_coord,y_coord,z_coord, rstride=1, cstride=1, 
            facecolors=fcolors, vmin=minn, vmax=maxx, shade=False)

# in order to always show the correct points on the sphere, 
# the points to be shown must be recalculated one the viewing angle changes
# when the user rotates the plot
def rotate(event):
    if event.inaxes == ax:
        plot_visible(ax.azim, ax.elev)

c1 = fig.canvas.mpl_connect('motion_notify_event', rotate)

plt.show()

В конце, возможно, придется немного поиграть с markersize, alpha и количество баллов, чтобы получить наиболее визуально привлекательный результат из этого.