Как называется этот алгоритм поиска?
Недавно я столкнулся с алгоритмом поиска чисел в отсортированном списке, и вот как он работает:
Дано: оракул, который сообщает вам, является ли данное число большим или меньшим, чем искомое число.
Начните с первого элемента в списке. Пропустите 1 элемент вперед и спросите оракула, опередили ли вы число, которое искали.
Если нет, попросите пропустить 2 элемента и спросите оракула, если вы зашли слишком далеко.
Если не пропустить 4 элемента впереди и т.д....
Когда вы найдете первый пропуск, который заставляет вас пропустить искомый номер, вы можете определить подинтервал, содержащий искомый номер.
Наконец, выполните бинарный поиск по подынтервалу.
Мне было интересно, как этот алгоритм назывался, чтобы я мог провести дополнительные исследования.
Спасибо
3 ответа
Вот как вы бинарный поиск неограниченного множества.
Например, решить неравенство f(n) < t над положительными целыми числами, где f - возрастающая функция.
Конкретный пример:
Solve n**2 + 10*n < 100 over the positive integers.
Let f(n) = n**2 + 10*n for n > 0
f is increasing because it's the sum of increasing functions.
f(1) = 1 + 10 = 11
f(2) = 4 + 20 = 24
f(4) = 16 + 40 = 56
f(8) = 64 + 80 = 144 > 100
Now we binary search the interval [4,8]
f(6) = 36 + 60 = 96
f(7) = 49 + 70 = 119 > 100
Thus n < 7
Я бы предложил несколько изменений в алгоритме. Должно быть 2 итератора, один за другим, и когда вы поймете, что перешли к узлу списка, который имеет большее число, чем искомый номер... мы должны повторить те же шаги с предыдущим итератором... это продолжается до тех пор, пока мы не найдем число.. потому что я не понимаю, как бы сделать двоичный поиск, то есть в журнале (N) время со списком...
Эта структура данных называется Skip Lists
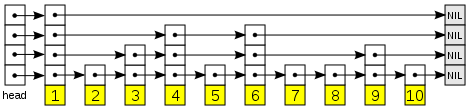
Список пропусков - это структура данных для хранения отсортированного списка элементов с использованием иерархии связанных списков, которые связывают все более разрозненные подпоследовательности элементов. Эти вспомогательные списки позволяют осуществлять поиск элементов с эффективностью, сравнимой с сбалансированными деревьями двоичного поиска (то есть с количеством проб, пропорциональных log n вместо n).