Matlab: решение логарифмического уравнения
У меня есть следующее уравнение, которое я хочу решить в отношении a:
x = (a-b-c+d)/log((a-b)/(c-d))
где x, b, c, а также d известны. Я использовал Wolfram Alpha для решения уравнения, и результат:
a = b-x*W(-((c-d)*exp(d/x-c/x))/x)
где W является функцией журнала продукта (W функция Ламберта). Это может быть легче увидеть на странице Wolfram Alpha.
Я использовал встроенный в Matlab lambertW Функция для решения уравнения. Это довольно медленно и является узким местом в моем сценарии. Есть ли другой, более быстрый, способ сделать это? Он не должен быть точным с точностью до десятого знака после запятой.
РЕДАКТИРОВАТЬ: я понятия не имел, что это уравнение так трудно решить. Вот картинка, иллюстрирующая мою проблему. Температуры bd плюс LMTD изменяются на каждом временном шаге, но известны. Тепло передается от красной линии (CO2) к синей линии (вода). Мне нужно найти температуру "а". Я не знал, что это так сложно рассчитать!:П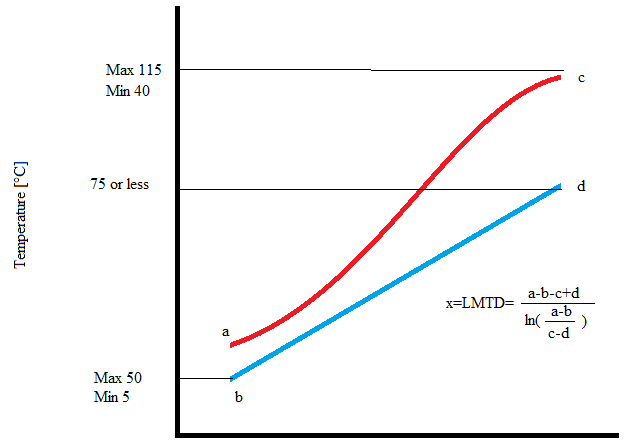
2 ответа
Другой вариант основан на более простой функции Wright ω:
a = b - x.*wrightOmega(log(-(c-d)./x) - (c-d)./x);
при условии, что d ~= c + x.*wrightOmega(log(-(c-d)./x) - (c-d)./x) (То есть, d ~= c+b-a, x является 0/0 в этом случае). Это эквивалентно главной ветви W- функции Ламберта, W 0, которая, я думаю, является той ветвью решения, которую вы хотите.
Так же, как с lambertW, есть wrightOmega функция в наборе инструментов Symbolic Math. К сожалению, это, вероятно, также будет медленным для большого количества входов. Тем не менее, вы можете использовать мой wrightOmegaq на GitHub для комплексных входных данных с плавающей точкой (двойной или одинарной точности). Функция более точная, полностью векторизованная и может быть на три-четыре порядка быстрее, чем при использовании встроенного wrightOmega для входов с плавающей точкой.
Для тех, кто заинтересован, wrightOmegaq основан на этой превосходной статье:
Пирс В. Лоуренс, Роберт М. Корлесс и Дэвид Дж. Джеффри, " Алгоритм 917: комплексная оценка двойной точности омега-функции Райта ", ACM транзакции по математическому программному обеспечению, Vol. 38, № 3, статья 20, с. 1-17, апрель 2012 г.
Этот алгоритм выходит за рамки кубической сходимости метода Галлея, используемого в Cleve Moler's Lambert_W и использует метод поиска корней с сходимостью четвертого порядка (Fritsch, Shafer, & Crowley, 1973), чтобы сходиться не более чем за две итерации.
Кроме того, для дальнейшего ускорения Moler's Lambert_W используя расширения серии, смотрите мой ответ на Math.StackExchange.
Два (комбинируемых) варианта:
- Ваш сценарий уже векторизован? Оцените функцию для более чем одного аргумента. проведение
for i = 1:100, a(i)=lambertw(rhs(i)); endмедленнее, чемa=lambertw(rhs), - Если вы имеете дело с реальным значением ветви LambertW (т.е. ваши аргументы находятся в интервале
[-1/e, inf)), вы можете использовать реализациюLambert_Wпредставленный Cleve Moler на Обмене файлами.
Знаете ли вы массовый расход с обеих сторон теплообменника на каждом шаге по времени? Если да, то температура "а" может быть решена с помощью подхода "эффективность-NTU", который не требует какой-либо итерации, а не подхода LMTD. Ссылка: например, http://ceng.tu.edu.iq/ched/images/lectures/chem-lec/st3/c2/Lec23.pdf