Внедрение SARSA с использованием Gradient Discent

Question

Я успешно реализовал алгоритм SARSA (как одношаговый, так и с использованием трасс приемлемости), используя поиск в таблице. По сути, у меня есть матрица q-значений, где каждая строка соответствует состоянию, а каждый столбец - действию.

Что-то вроде:

[Q(s1,a1), Q(s1,a2), Q(s1,a3), Q(s1,a4)]
[Q(s2,a1), (Q(s2,a2), Q(s2a3), Q(s2, a2]
.
.
.
[Q(sn,a1), Q(sn,a2), Q(sn,a3), Q(sn,a4)]

На каждом временном шаге выбирается строка из матрицы, и, в зависимости от политики, действие выбирается и обновляется в соответствии с правилами SARSA.

Сейчас я пытаюсь реализовать его как нейронную сеть с использованием градиентного спуска.

Моя первая гипотеза состояла в том, чтобы создать двухслойную сеть, в которой входной слой имел бы столько входных нейронов, сколько имеется состояний, а выходной слой имел столько выходных нейронов, сколько было действий. Каждый вход будет полностью подключен к каждому выходу. (Так, на самом деле, это будет выглядеть как матрица выше)

Мой входной вектор был бы вектором строки 1xn, где n - количество входных нейронов. Все значения во входном векторе будут равны 0, за исключением индекса, соответствующего текущему состоянию, которое будет равно 1. Т.е.

[0 0 0 1 0 0]

Будет входным вектором для агента в состоянии 4.

Итак, процесс будет примерно таким:

[0 0 0 1 0 0] X [ 4 7 9 3]
                [ 5 3 2 9]
                [ 3 5 6 9]
                [ 9 3 2 6]
                [ 2 5 7 8]
                [ 8 2 3 5]

Где я создал случайную, весовую матрицу выборки.

Результат будет:

[9 3 2 6]

Это означает, что если была выбрана жадная политика, должно быть выбрано действие 1, и связь между четвертым входным нейроном и первым выходным нейроном должна стать сильнее:

dw = dw_old + learning_rate*(reward + discount*network_output - dw_old)

(Уравнение взято из алгоритма SARSA)

ОДНАКО - эта реализация не убеждает меня. Согласно тому, что я прочитал, сетевые веса должны использоваться для вычисления Q-значения пары состояние-действие, но я не уверен, что они должны представлять такие значения. (Особенно потому, что я обычно видел значения веса, включенные только между 0 и 1.)

Любой совет?

Answer 1

Резюме: ваш текущий подход верен, за исключением того, что вы не должны ограничивать свои выходные значения между 0 и 1.

На этой странице есть отличное объяснение, которое я приведу здесь. В нем конкретно не обсуждается SARSA, но я думаю, что все, что он говорит, должно переводиться.

Значения в векторе результатов должны действительно представлять оценки вашей нейронной сети для значений Q, связанных с каждым состоянием. По этой причине обычно рекомендуется не ограничивать диапазон допустимых значений значениями от нуля до единицы (поэтому просто суммируйте значения, умноженные на вес соединения, вместо использования какой-либо функции активации сигмоида).

Что касается того, как представлять состояния, одним из вариантов является их представление в терминах датчиков, которые агент имеет или может теоретически иметь. Например, в приведенном ниже примере робот имеет три "щупальцевых" датчика, каждый из которых может находиться в одном из трех условий. Вместе они предоставляют роботу всю информацию, которую он собирается получить, в каком состоянии он находится.

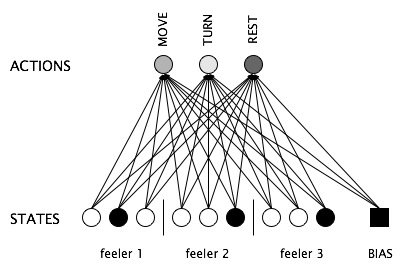
Однако, если вы хотите предоставить своему агенту точную информацию, вы можете себе представить, что у него есть датчик, который точно сообщает ему, в каком состоянии он находится, как показано в конце этой страницы. Это будет работать точно так, как настроена ваша сеть, с одним входом, представляющим каждое состояние.