Уточнение STFT (FFT для ввода в реальном времени)
Я понимаю, как работает ДПФ с помощью корреляции, и использую его в качестве основы для понимания результатов БПФ. Если у меня есть дискретный сигнал, который был дискретизирован с частотой 44,1 кГц, то это означает, что если бы я брал 1 с данных, у меня было бы 44 100 выборок. Чтобы запустить FFT, мне понадобится массив из 44 100 и DFT с N=44 100, чтобы получить разрешение, необходимое для обнаружения частот до 22 кГц, верно? (Поскольку БПФ может коррелировать вход только с синусоидальными компонентами до частоты N/2)
Это, очевидно, много точек данных и времени вычислений, и я прочитал, что именно здесь вступает в действие короткое время FT (STFT). Если я тогда возьму первые 1024 выборки (~23 мс) и запусту FFT на этом, то Взяв перекрывающиеся 1024 выборки, я могу получить непрерывную частотную область сигнала каждые 23 мс. Тогда как мне интерпретировать вывод? Если выходной сигнал БПФ для статических данных составляет N / 2 точек данных с полосой пропускания fs/(N/2), какова ширина полосы частотного выхода STFT?
Вот пример, который я запускал в Mathematica:
100 Гц синусоида с частотой дискретизации 44,1 кГц: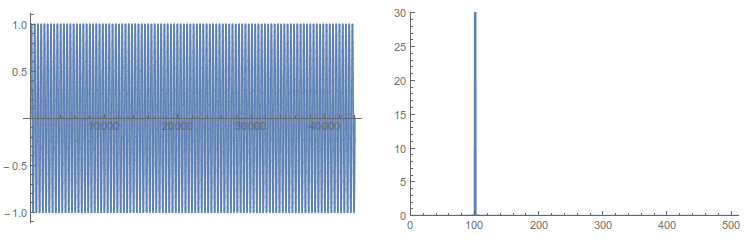
Затем я запускаю БПФ только на первых 1024 точках: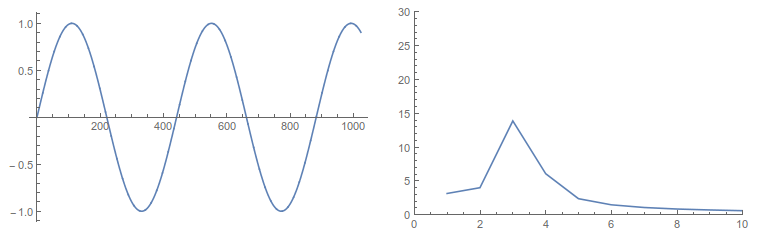
Частота интереса тогда находится в точке данных 3, которая должна как-то соответствовать 100 Гц. Я думаю, что 44100/1024 = 43 - это что-то вроде коэффициента масштабирования, который означает, что сигнал с частотой 1 Гц в этом маленьком окне будет соответствовать сигналу с частотой 43 Гц в полном массиве данных. Тем не менее, это даст мне выход 43 Гц *3 = 129 Гц. Правильна ли моя логика, но не моя реализация?
1 ответ
Как я уже говорил в моих предыдущих комментариях, переменная N влияет на разрешение, достигаемое спектром выходной частоты, а не на диапазон частот, которые вы можете обнаружить. Чем больше N, тем выше разрешение за счет более высокого времени вычислений и меньшего времени. N дает вам меньшее время вычислений, но может вызвать спектральную утечку, что является эффектом, который вы видели на своем последнем рисунке.
Что касается вашего другого вопроса, теоретически полоса пропускания БПФ бесконечна, но мы ограничиваем наш результат полосой частот в диапазоне [-fs/2 до fs/2], поскольку все частоты вне этой полосы восприимчивы к псевдонимы и, следовательно, бесполезны. Кроме того, если входной сигнал является реальным (что верно в большинстве случаев, в том числе и у нас), то частоты от [-fs/2 до 0] являются просто отражением частот от [0 до fs/2], и поэтому некоторые процедуры FFT просто выводят спектр FFT от [0 до fs/2], что, я думаю, применимо к вашему случаю. Это означает, что N / 2 точек данных, которые вы получили в качестве выходных данных, представляют частоты в диапазоне [0 - fs/2], так что это полоса пропускания, с которой вы работаете в случае FFT, а также в случае STFT (STFT - это просто серия FFT, каждый FFT в STFT даст вам спектр с точками данных в этой полосе).
Я также хотел бы отметить, что STFT, скорее всего, не сократит ваше время вычислений, если ваш входной сигнал представляет собой изменяющийся сигнал, такой как музыка, потому что в этом случае вам потребуется выполнить его несколько раз в течение всей песни, чтобы он Однако это поможет вам лучше понять частотные характеристики вашей песни, чем если бы вы только что исполнили одно БПФ.
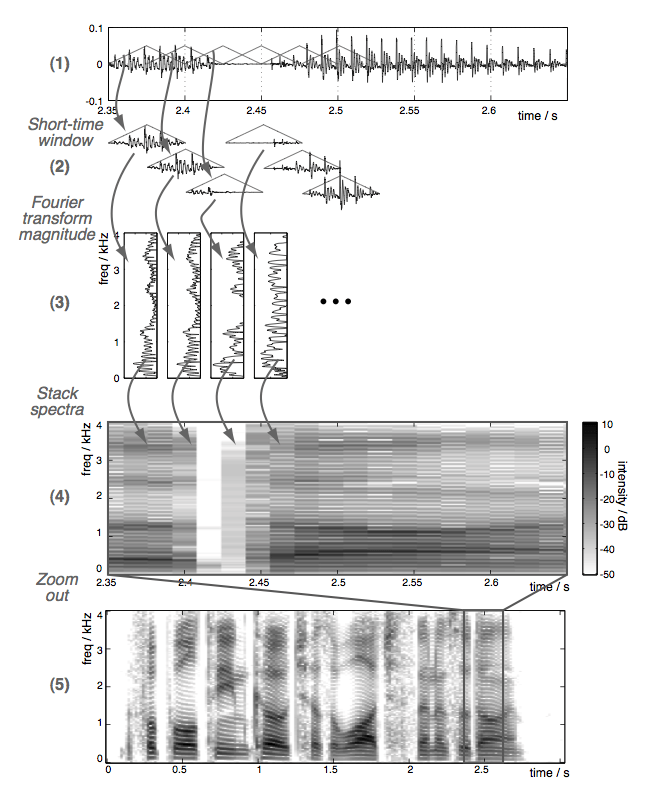
Чтобы визуализировать результаты БПФ, вы используете графики частотного (и / или фазового) спектра, но для визуализации результатов БПФ вам, скорее всего, потребуется создать спектрограмму, которая в основном представляет собой график, который можно получить, просто поместив отдельные спектры БПФ бок о бок. Процесс создания спектрограммы можно увидеть на рисунке ниже (Источник: Дэн Эллис - Введение в обработку речи). Спектрограмма покажет вам, как частотные характеристики вашего сигнала меняются со временем и как вы их интерпретируете будет зависеть от того, какие конкретные функции вы хотите извлечь / обнаружить из аудио. Возможно, вы захотите взглянуть на страницу википедии спектрограммы для получения дополнительной информации.