Объяснение алгоритма "Граф эскиза"
Может кто-нибудь объяснить, как работает алгоритм Sketch Count? Я до сих пор не могу понять, например, как используются хеши. Мне трудно понять эту статью.
2 ответа
Этот алгоритм потоковой передачи создает следующую структуру.
Найдите алгоритм рандомизированной потоковой передачи, выход которого (как случайная величина) имеет желаемое ожидание, но обычно высокую дисперсию (т. Е. Шум).
Чтобы уменьшить дисперсию / шум, запустите много независимых копий параллельно и объедините их выходные данные.
Обычно 1 интереснее, чем 2. Этот алгоритм 2 на самом деле несколько нестандартный, но я собираюсь поговорить только о 1.
Предположим, мы обрабатываем ввод
a b c a b a .
С тремя счетчиками нет необходимости хешировать.
a: 3, b: 2, c: 1
Предположим, однако, что у нас есть только один. Есть восемь возможных функций h : {a, b, c} -> {+1, -1}, Вот таблица результатов.
h |
abc | X = counter
----+--------------
+++ | +3 +2 +1 = 6
++- | +3 +2 -1 = 4
+-- | +3 -2 -1 = 0
+-+ | +3 -2 +1 = 2
--+ | -3 -2 +1 = -4
--- | -3 -2 -1 = -6
-+- | -3 +2 -1 = -2
-++ | -3 +2 +1 = 0
Теперь мы можем рассчитать ожидания
(6 + 4 + 0 + 2) - (-4 + -6 + -2 + 0)
E[h(a) X] = ------------------------------------ = 24/8 = 3
8
(6 + 4 + -2 + 0) - (0 + 2 + -4 + -6)
E[h(b) X] = ------------------------------------ = 16/8 = 2
8
(6 + 2 + -4 + 0) - (4 + 0 + -6 + -2)
E[h(c) X] = ------------------------------------ = 8/8 = 1 .
8
Что тут происходит? За aскажем, мы можем разложить X = Y + Z, где Y это изменение суммы для aс и Z сумма для неas. По линейности ожидания мы имеем
E[h(a) X] = E[h(a) Y] + E[h(a) Z] .
E[h(a) Y] сумма с термином для каждого вхождения a то есть h(a)^2 = 1, так E[h(a) Y] это число вхождений a, Другой термин E[h(a) Z] ноль; даже учитывая h(a)хэш-значения друг друга с равной вероятностью могут быть плюс или минус один и, следовательно, дают нулевое ожидание.
На самом деле хеш-функция не обязательно должна быть однородной случайной, и это хорошая вещь: не было бы способа ее сохранить. Достаточно, чтобы хеш-функция была попарно независимой (любые два конкретных хеш-значения независимы). Для нашего простого примера достаточно случайного выбора следующих четырех функций.
abc
+++
+--
-+-
--+
Я оставлю вам новые расчеты.
Эскиз подсчета - это вероятностная структура данных, которая позволяет ответить на следующий вопрос:
Чтение потока элементов a1, a2, a3, ..., an там, где может быть много повторяющихся элементов, в любое время он даст вам ответ на следующий вопрос: сколько ai элементы вы уже видели.
Вы можете четко получить точное значение в любое время, просто поддерживая хэш, где ключи являются вашими ai и значения - это то, сколько элементов вы уже видели. Это быстро O(1) добавлять, O(1) проверьте, и это даст вам точный счет. Единственная проблема, которая требуется O(n) пробел, где n - количество отдельных элементов (имейте в виду, что размер каждого элемента имеет большую разницу, потому что он занимает way more space to store this big string as a key чем просто this,
Так как граф Скетч поможет тебе? Как и во всех вероятностных структурах данных, вы жертвуете определенностью для пространства. Эскиз подсчета позволяет выбрать 2 параметра: точность результатов ε и вероятность неверной оценки δ.
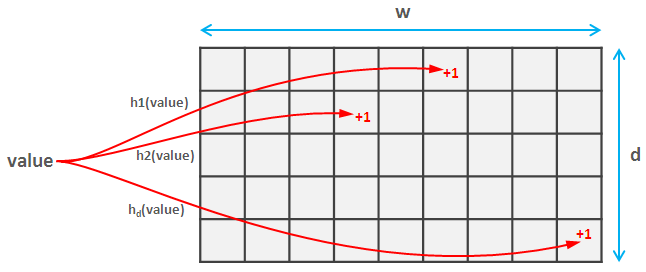
Для этого вы выбираете семью d попарно независимые хеш-функции. Эти сложные слова означают, что они не сталкиваются часто (фактически, если оба хэша отображают значения в пространство [0, m] вероятность столкновения составляет примерно 1/m^2). Каждая из этих хеш-функций отображает значения в пространство [0, w], Итак, вы создаете d * w матрица.
Теперь, когда вы читаете элемент, вы рассчитываете каждый из d хэши этого элемента и обновите соответствующие значения в эскизе. Эта часть одинакова для графического эскиза и графического эскиза.
Insomniac хорошо объяснил идею (вычисление ожидаемого значения) для эскиза счета, поэтому я просто скажу, что с помощью счетчика-минут все еще проще. Вы просто вычисляете d хешей значения, которое хотите получить, и возвращаете наименьшее из них. Удивительно, но это дает надежную гарантию точности и вероятности, которую вы можете найти здесь.
Увеличение диапазона хэш-функций, повышение точности результатов, увеличение количества хеш-функций снижает вероятность неверной оценки: ε = e/w и δ=1/e^d. Другая интересная вещь заключается в том, что значение всегда завышено (если вы нашли значение, оно, скорее всего, больше реального значения, но, конечно, не меньше).
На самом деле, хеш-функция не обязательно должна быть однородной случайной, и это хорошая вещь: не было бы способа ее сохранить. Достаточно, чтобы хеш-функция была попарно независимой (любые два конкретных хеш-значения независимы). Для нашего простого примера достаточно случайного выбора следующих четырех функций.