Алгоритм Флойда – Варшалла с реконструкцией пути не находит путь
Я пытаюсь найти кратчайший путь между источником и целью, используя алгоритм Флойда-Варшалла, вычисляя кратчайшие пути между всеми парами.
Мне нужно найти кратчайший путь, а не только расстояние. Вот что я пытаюсь сделать:
Я храню первую вершину на кратчайшем пути от i до j. Всякий раз, когда кратчайший путь от i до j обновляется, и теперь он проходит через k, я устанавливаю первую вершину на кратчайшем пути от i до j к этому на кратчайшем пути от i до k.
/*first[i][j] is the first vertex after i on the shortest path from i to j.
first[i][j] is initially j if there is an edge from i to j and the dist[i][j] is the weight of the edge. Otherwise f[i][j] is -1 and the cost is infinity.
*/
for(k = 0; k < N; ++k){
for(i = 0; i < N; ++i){
for(j = 0; j < N; ++j){
if(dist[i][j] >= dist[i][k]+dist[k][j]){
dist[i][j] = dist[i][k]+dist[k][j];
//When the distance is updated, update first[i][j]
first[i][j] = first[i][k];
}
}
}
}
Проблема с этим алгоритмом состоит в том, что когда я запускаю этот алгоритм на следующем графике, путь, найденный этим алгоритмом, представляет собой бесконечный цикл.
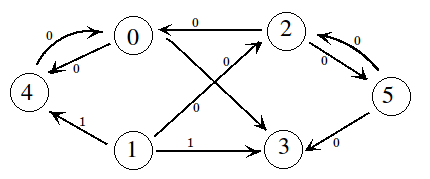
Здесь first Матрица рассчитывается по алгоритму:
4 4 4 4 4 4
2 2 2 2 2 2
5 5 5 5 5 5
1 1 1 1 1 1
0 0 0 0 0 0
2 2 2 2 2 2
Первая вершина на кратчайшем пути от 0 до любой другой вершины, согласно алгоритму, равна 4, но первая вершина на кратчайшем пути от 4 до любой другой вершины равна 0.
- Почему этот алгоритм ведет себя таким образом?
- Есть ли другой способ вычислить первую (после исходного) вершину на каждом пути, пока я вычисляю длину пути?
Я прочитал статью в Википедии, а также некоторые вопросы по SO, но они не сильно помогли.
1 ответ
Ваш dist Матрица уже, кажется, рассчитана правильно, но ваш first Кажется, что у матричных дополнений есть проблема с ребрами нулевой стоимости.
Посмотрите на эту слегка модифицированную версию Python вашего кода, которая использует 0.01 как стоимость для всех само-ребер и других ребер с нулевой стоимостью.
Этот код выводит (надеюсь) правильный dist а также first матрицы
[0.01, inf, inf, 0.01, 0.01, inf]
[0.02, 0.01, 0.01, 0.01, 0.03, 0.02]
[0.01, inf, 0.01, 0.02, 0.02, 0.01]
[ inf, inf, inf, 0.01, inf, inf]
[0.01, inf, inf, 0.02, 0.01, inf]
[0.02, inf, 0.01, 0.01, 0.03, 0.01]
а также
[ 0, None, None, 3, 4, None]
[ 2, 1, 2, 3, 2, 2]
[ 0, None, 2, 5, 0, 5]
[None, None, None, 3, None, None]
[ 0, None, None, 0, 4, None]
[ 2, None, 2, 3, 2, 5]