Форма неба кажется неправильной в Скайфилде - мой питон правильный?

Question

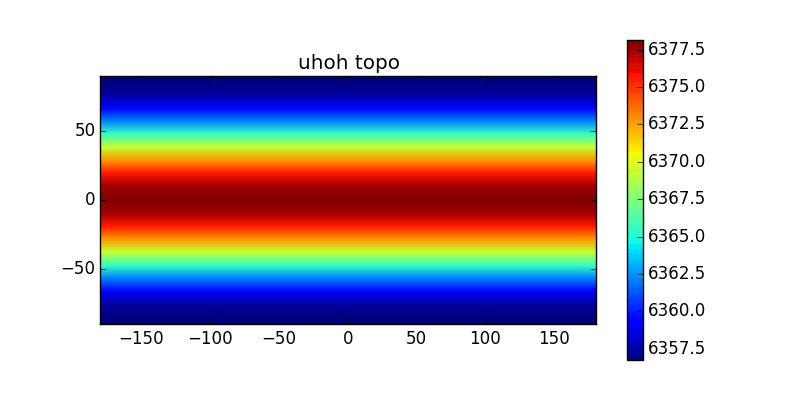
Отображение расстояния от центра Земли до различных (lat, lon) положения с использованием Skyfield показывают изменение с широтой, но независимо от долготы (субмиллиметр). Это может быть документированное приближение в пакете, ошибка в моем скрипте или что-то еще в целом. Я что-то здесь не так делаю? (кроме того, конечно, используя самолет)

import numpy as np
import matplotlib.pyplot as plt
from skyfield.api import load, now

data  = load('de421.bsp')
earth = data['earth']
jd    = now()

epos = earth.at(jd).position.km

lats = np.linspace( -90,  90, 19)
lons = np.linspace(-180, 180, 37)
LATS, LONS = np.meshgrid(lats, lons)

s = LATS.shape

points = zip(LATS.flatten(), LONS.flatten())

rr = []
for point in points:
    la, lo = point
    pos = earth.topos(la, lo).at(jd).position.km
    r   = np.sqrt( ((pos-epos)**2).sum() )
    rr.append(r)

surf = np.array(rr).reshape(s)

extent = [lons.min(), lons.max(), lats.min(), lats.max()]

plt.figure()
plt.imshow(surf.T, origin='lower', extent=extent)
plt.colorbar()
plt.title('uhoh topo')
plt.savefig('uhoh topo')
plt.show()

В качестве перекрестной проверки я попробовал несколько случайных пар местоположений с одинаковой широтой:

pe = earth.at(jd).position.km
for i in range(10):

    lon1, lon2 = 360.*np.random.random(2)-180
    lat = float(180.*np.random.random(1)-90.)

    p1  = earth.topos(lat, lon1).at(jd).position.km
    p2  = earth.topos(lat, lon2).at(jd).position.km

    r1   = np.sqrt( ((p1-pe)**2).sum() )
    r2   = np.sqrt( ((p2-pe)**2).sum() )

    print lat, lon1, lon2, r2-r1

и получил это (четвертый столбец показывает разницу в микронах):

45.8481950437 55.9538249618 115.148786114 1.59288902069e-08
-72.0821405192 4.81264755835 172.783338907 2.17096385313e-09
51.6126938075 -54.5670258363 -134.888403816 2.42653186433e-09
2.92691713179 -178.553103457 134.648099589 1.5916157281e-10
-78.7376163827 -55.0684703115 125.714124504 -6.13908923697e-10
48.5852207923 -169.061708765 35.5374862329 7.60337570682e-10
42.3767785876 130.850223447 -111.520896867 -1.62599462783e-08
11.2951212126 -60.0296460731 32.8775784623 6.91579771228e-09
18.9588262131 71.3414406837 127.516370219 -4.84760676045e-09
-31.5768658495 173.741960359 90.3715297869 -6.78483047523e-10

Answer 1

topos() метод включает в себя elevation_m=0.0 что вы не указываете. Таким образом, для каждого из ваших вызовов значение по умолчанию составляет 0,0 метра над уровнем моря. И определение "уровня моря" не меняется с долготой - на данной широте уровень моря находится на фиксированном расстоянии от геоцентра по всему миру.

Я не уверен, почему вы называете ошибку микронного уровня "довольно большим приближением", но вы действительно сталкиваетесь с ограниченной точностью 64-битной математики вашей машины, когда вычитаете два расстояния, каждое из которых имеет длину около 1 а.е. - вы видите ошибку округления вниз в последнем бите или два.