Интерполяция и экстраполяция случайно рассеянных данных в равномерную сетку в 3D

Question

У меня есть сетка 256 x 256 x 32 с регулярно расположенными точками в диапазоне x, y и z и соответствующей переменной "a". У меня также есть группа случайно разбросанных точек в более узком пространстве x, y, z со связанной переменной "b". По сути, я хочу интерполировать и экстраполировать мои случайные данные на сетку с регулярным интервалом, которая соответствует кубу "а", как показано ниже:

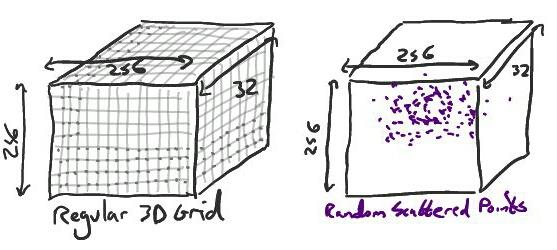
До сих пор я использовал griddata scipy для достижения интерполяции, которая, кажется, работает нормально, но она не может справиться с экстраполяцией (насколько я знаю), и результат резко усекается до значений 'nan'. Во время исследования этой проблемы я столкнулся с парой людей, использующих griddata во второй раз с "ближайшим" в качестве метода интерполяции для заполнения значений "nan". Я пробовал это, но результаты не кажутся надежными. Более подходящие результаты получаются, если я использую fill_Value с "линейным" режимом, но на данный момент это больше помадка, потому что fill_Value должен быть константой.

Я заметил, что в MATLAB есть класс ScatteredInterpolant, который, кажется, делает то, что я хочу, но я не могу найти эквивалентный класс в Python или выяснить, как эффективно реализовать такую ​​процедуру в 3D. Любая помощь с благодарностью.

Код, который я использую для интерполяции, приведен ниже:

x, y, z, b = np.loadtxt(scatteredfile, unpack = True)

# Create cube to match aCube dimensions
xi = np.linspace(-xmax_aCube, xmax_aCube, 256)
yi = np.linspace(-ymax_aCube, ymax_aCube, 256)
zi = np.linspace(zmin_aCube, zmax_aCube, 32)

# Interpolate scattered points
X, Y, Z = np.meshgrid(xi, yi, zi)
bCube = griddata((x, y, z), b, (X, Y, Z), method = 'linear')    

Answer 1

Это обсуждение применимо в любой размерности. Для вашего трехмерного случая давайте сначала поговорим о вычислительной геометрии, чтобы понять, почему часть региона дает NaN от griddata,

Рассеянные точки в вашем объеме составляют выпуклый корпус; геометрическая форма со следующими свойствами:

• Поверхность всегда выпуклая (как следует из названия)
• Объем формы минимально возможен без нарушения выпуклости
• Поверхность (в 3d) триангулирована и замкнута

Менее формально выпуклый корпус ( который вы можете легко вычислить с помощью scipy) похож на растягивание воздушного шара над рамой, где углы рамки являются крайними точками вашего рассеянного скопления.

В обычном месте сетки внутри воздушного шара вы окружены известными точками. Вы можете интерполировать в эти места. За пределами этого вы должны экстраполировать.

Экстраполяция это сложно. Там нет общего правила, как это сделать... это зависит от конкретной проблемы. В этом регионе алгоритмы, такие как griddata выбрать, чтобы вернуться NaN - это самый безопасный способ сообщить ученому, что он должен выбрать разумный способ экстраполяции.

Давайте рассмотрим несколько способов сделать это.

1. [WORST] Обманите это

Назначьте некоторое скалярное значение вне корпуса. В кратких документах вы увидите, что это делается с помощью: s = mean(b) bCube = griddata((x, y, z), b, (X, Y, Z), method = 'linear', fill_value=s)

Минусы: это приводит к резкому разрыву в интерполированном поле на границе корпуса, сильно смещает среднее значение скалярного поля и не учитывает функциональную форму данных.

2. [СЛЕДУЮЩИЙ МИР] "Смешанный дурак"

Предположим, что в углах вашего домена вы применяете некоторую ценность. Это может быть среднее значение скалярного поля, связанного с вашими рассеянными точками.

Извините, это псевдокод, поскольку я вообще не использую numpy, но, вероятно, это будет довольно ясно.

# With a unit cube, and selected scalar value
x, y, z, b = np.loadtxt(scatteredfile, unpack = True)
s = mean(b)
x.append([0 0 0 0 1 1 1 1])
y.append([0 0 1 1 0 0 1 1])
z.append([0 1 0 1 0 1 0 1])
b.append([s s s s s s s s])
# drop in the rest of your code

Минусы: это приводит к резкому разрыву градиента интерполированного поля на границе корпуса, довольно сильно смещает среднее значение скалярного поля и не учитывает функциональную форму данных.

3. [Все еще ПЛОХО ПЛОХО] Ближайший сосед

Для каждой из обычных точек NaN найдите ближайшее не-NaN и присвойте это значение. Это эффективно и стабильно, но грубо, потому что ваше поле может в конечном итоге иметь узорные элементы (например, полосы или лучи, выходящие из корпуса), часто визуально непривлекательные или, что еще хуже, неприемлемые с точки зрения гладкости данных

В зависимости от плотности данных вы можете использовать ближайшую рассеянную точку данных вместо ближайшей не-NaN регулярной точки. Это может быть сделано просто (опять же, псевдокод):

bCube = griddata((x, y, z), b, (X, Y, Z), method = 'linear', fill_value=nan)
bCubeNearest = griddata((x, y, z), b, (X, Y, Z), method = 'nearest')
indicesMask = isNan(bCube)
# Use nearest interpolation outside the hull, keeping linear interpolation inside.
bCube(indicesMask) = bCubeNearest(indicesMask)

Использование подходов MATLAB на основе delaunay покажет более мощные методы для достижения подобного в однострочнике, но здесь numpy выглядит немного ограниченным.

4. [НЕ ВСЕГДА УЖАСНО] Естественно взвешенный

Извините за плохое объяснение в этом разделе, я никогда не писал алгоритм, но я уверен, что некоторые исследования техники естественного соседа помогут вам далеко

Используйте функцию взвешивания расстояния с некоторым параметром D, который может быть примерно или вдвое больше (скажем) длины вашей коробки. Вы можете настроить. Для каждого местоположения NaN определите расстояние до каждой точки рассеяния.

# Don't do it this way for anything but small matrices - this is O(NM) 
# and it can be done much more effectively (e.g. MATLAB has a quick 
# natural weighting option), but for illustrative purposes:
for each NaN point 1:N
    for each scattered point 1:M
        calculate a basis function using inverse distance from NaN to point, normalised on D, and store in a [1 x M] vector of weights
Multiply weights by the b value, summate and divide by M   

В основном вы хотите получить функцию, которая плавно переходит к средней интенсивности B на расстоянии D от корпуса, но совпадает с оболочкой на границе. Вдали от границы он наиболее сильно взвешен в ближайших точках.

Плюсы: приятно стабильные и достаточно продолжительные. Из-за взвешивания более устойчив к шуму в отдельных точках данных, чем ближайший сосед.

5. [HEROIC ROCKSTAR] Допущение функциональной формы

Что вы знаете о физике? Предположим, что функциональная форма представляет то, что вы ожидаете от физики, затем выполните наименьшие квадраты (или какой-нибудь эквивалент) для подгонки этой формы к разбросанным данным. Используйте функцию для стабилизации экстраполяции.

Несколько хороших идей, которые могут помочь вам построить функцию:

• Ожидаете ли вы симметрию или периодичность?
• Является ли компонент ba векторного поля, обладающего некоторым свойством, например, нулевой дивергенцией?
• Направленность: ожидаете ли вы, что все углы будут одинаковыми? Или, может быть, линейное изменение в одном направлении?
• находится ли поле b в определенный момент времени - возможно, можно использовать сглаженную серию измерений, чтобы придумать основную функцию?
• Существует ли уже известная форма, подобная гауссовой или квадратичной?

Некоторые примеры:

• b представляет интенсивность лазерного луча, проходящего через объем. Вы ожидаете, что входная сторона будет номинально идентична выходной, а остальные четыре границы нулевой интенсивности. Интенсивность будет иметь концентрический гауссов профиль.

• b является одной из составляющих поля скоростей в несжимаемой жидкости. Жидкость должна быть бездивергентной, поэтому любое месторождение в зоне NaN также должно быть бездивергентным, чтобы вы применили это условие.

• б представляет температуру в комнате. Вы ожидаете более высокую температуру наверху, потому что горячий воздух поднимается.

• b представляет подъемную силу на аэродинамической поверхности, проверенную по трем независимым переменным. Вы можете легко найти лифт в стойле, поэтому точно знайте, что будет в некоторых частях пространства.

Плюсы / минусы: поймите это правильно, и это будет здорово. Поймите это неправильно, особенно с нелинейными функциональными формами, и это пойдет очень неправильно и может привести к очень нестабильным результатам.

Предупреждение о вреде для здоровья: вы не можете принять функциональную форму, получить симпатичные результаты, а затем использовать их, чтобы доказать, что функциональная форма верна. Это просто плохая наука. Форма должна быть чем-то хорошим и известным независимо от вашего анализа данных.

Answer 2

Если ваш разброс точек достаточно хорошо соответствует форме куба, одним из подходов может быть использование griddata интерполировать на регулярную сетку данных, которая вписывается в ваше облако точек (следовательно, избегая nans), а затем использовать эту регулярную сетку значений в качестве входных данных для interpn что облегчает линейную экстраполяцию (но требует регулярной сетки в качестве входных данных).

Таким образом, вы можете использовать griddata как и раньше для всех точек внутри выпуклой оболочки вашего разброса точек, и вы можете использовать interpn оценить точки, которые возвращаются как нанс.

Это далеко не идеально, но я думаю, что это ближе к достижению того, что вы ищете.

Плюсы:

• Избегает резких разрывов.
• Захватывает основные линейные тренды на границе вашего набора данных, не зная функциональной формы.
• Учитывает асимметрию в ваших данных (например, не имеет тенденцию к значению совокупности на больших расстояниях, поэтому одна сторона вашего набора данных может иметь большие значения, чем другая на больших расстояниях.)

Минусы:

• Эффективность этого подхода будет во многом зависеть от того, насколько большой куб вы можете поместить в выпуклую оболочку вашего первоначального разброса точек. Если ваши данные являются заостренными / неоднородными и нерегулярными, то даже точки на краю выпуклого корпуса могли быть экстраполированы на значительные расстояния от края вложенного куба, что приводило к ошибкам, поскольку при экстраполяции не учитывались более близкие точки данных, лежащие вне куба.
• Линейная экстраполяция будет сильно зависеть от шума в данных на краях облака точек.
• Вычислительная стоимость выполнения двух наборов интерполяций.