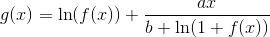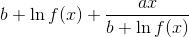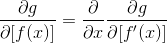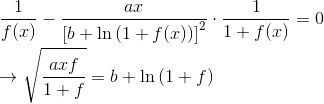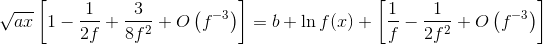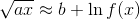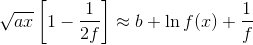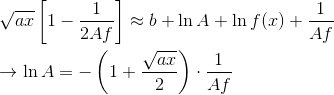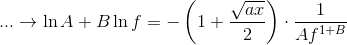Какой f(x) минимизирует порядок g(f(x)), так как x уходит в бесконечность

Question

Предположим, что f (x) стремится к бесконечности, поскольку x стремится к бесконечности и a,b>0. Найдите f (x), который дает самый низкий порядок для

как х стремится к бесконечности. Под порядком я подразумеваю обозначения Big O и Little O.

Я могу только решить это примерно:

Мое решение: мы можем сказать, что ln(1+f(x)) приблизительно равно ln (f (x)), поскольку x стремится к бесконечности. Затем я должен минимизировать порядок

Поскольку для любого c>0 y+c/y уменьшается, когда y =sqrt(c), b+ln f(x)}=sqrt(ax) - ответ. Эквивалентно, f(x)=e^(sqrt(ax)-b) и самый низкий порядок для g (x) составляет 2 sqrt(ax).

Можете ли вы помочь мне получить точный ответ?

Answer 1

Строгий способ минимизировать (я бы сказал, экстремизировать) функцию другой функции заключается в использовании отношения Эйлера-Лагранжа:

Таким образом:

Расширение Тейлора:

Если мы рассмотрим только до "постоянных" условий:

Что, конечно, результат, который вы получили.

---

Далее линейные условия:

Мы не можем решить это уравнение аналитически; но мы можем исследовать влияние возмущения в функции f(x) (т.е. небольшое изменение параметра по сравнению с предыдущим решением). Очевидно, мы можем игнорировать любые линейные изменения f, но мы можем добавить положительный мультипликативный фактор A:

sqrt(ax) а также Af очевидно, оба положительные, поэтому RHS имеет отрицательный знак. Это означает, что ln(A) < 0, и поэтому A < 1новая возмущенная функция дает (немного) более узкую границу. Так как RHS должен быть исчезающе маленьким (1/f), A не должен быть намного меньше 1.

Идя дальше, мы можем добавить еще одно возмущение B к показателю f:

поскольку ln(A) и RHS оба исчезают маленькими, B-термин на LHS должен быть еще меньше, чтобы знак был последовательным.

Таким образом, мы можем сделать вывод, что (1) A очень близко к 1, (2) B намного меньше, чем 1, то есть результат, который вы получили, на самом деле является очень хорошей верхней границей.

Сказанное также приводит к возможности еще более жестких границ для более высоких степеней f,