Существуют ли условия, при которых поддеревья, порожденные спектральным (вектором Фидлера), разъединяются?

Question

Я пытаюсь разделить неориентированное дерево на два поддерева, где каждое поддерево связано. Насколько я понимаю, это можно сделать, используя вектор Фидлера, как описано здесь. Однако, когда я следую этому процессу, полученные поддеревья не связаны.

Код, который я использовал для реализации деления пополам, приведен ниже, и здесь определяется дерево, которое не разбивается пополам.

import networkx as nx
from itertools import compress

g = nx.from_dict_of_dicts(broken_g)

def split_graph(graph):
    """Split a graph into two pieces using the Fiedler vector.

    See https://en.wikipedia.org/wiki/Graph_partition#Fiedler_eigenvalue_and_eigenvector
    """

    assert nx.is_connected(graph), 'must pass connected graph'

    fiedler_vec = nx.fiedler_vector(graph, normalized=True, weight=False)

    mask_a = fiedler_vec > 0
    mask_b = ~ mask_a

    subgraph_a_nodes = compress(graph.nodes(), mask_a)
    subgraph_b_nodes = compress(graph.nodes(), mask_b)

    subgraph_a = graph.subgraph(subgraph_a_nodes)
    subgraph_b = graph.subgraph(subgraph_b_nodes)

    assert nx.is_connected(subgraph_a) and nx.is_connected(subgraph_b), 'split did not produce connected subgraphs'

    return [subgraph_a, subgraph_b]

split_graph(g)

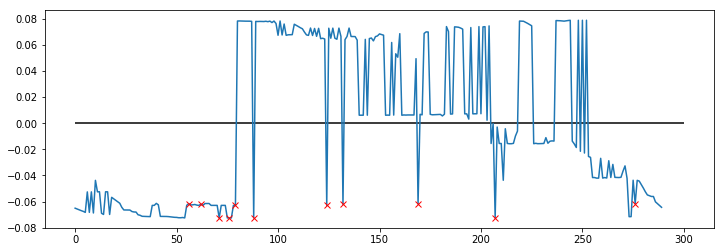
Когда я запускаю это, ни одно из полученных поддеревьев не подключается - каждое поддерево имеет один или два больших связанных компонента и несколько изолированных узлов. Построение значений вектора Фидлера и определение изолированных узлов выглядит следующим образом:

Что здесь происходит?

Answer 1

Одной из характеристик дерева является то, что между каждой парой вершин в дереве существует только один путь. В результате, когда ребро обрезается, вершины, которые были на этом ребре, больше не связаны, так как это был их единственный путь. Поскольку связность коммутативна, каждая вершина на одной стороне разреза отсоединяется от каждой вершины на другой стороне разреза. В результате вы всегда разделяете дерево на два подключенных поддерева, когда вы обрезаете один край. Глядя на эту страницу википедии, кажется, что использование спектрального деления может привести к решениям, которые срезают несколько ребер. По существу, любое деление пополам, которое обрезает более 1 края, приведет к созданию более 2 связанных поддеревьев.