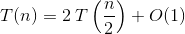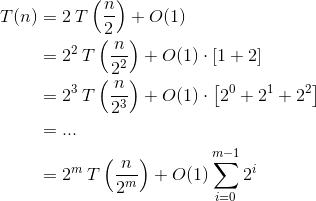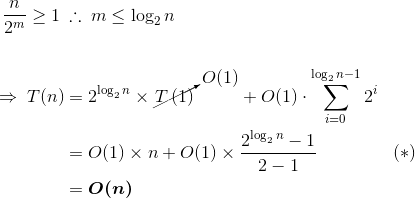Big O Рекурсивный метод

Question

У меня есть метод под названием бинарная сумма

Algorithm BinarySum(A, i, n):
Input: An array A and integers i and n
Output: The sum of the n integers in A starting at index i
if n = 1 then
    return A[i]
return BinarySum(A, i, n/ 2) + BinarySum(A, i + n/ 2, n/ 2)

Игнорируя факт усложнения простой задачи, меня попросили найти Большой О. Вот мой мыслительный процесс. Для массива размера NI будет делать 1 + 2 + 4 .. + N рекурсивных вызовов. Это почти половина суммы от 1 до N, поэтому я скажу, что это примерно N(N + 1)/4. Сделав так много звонков, мне нужно сложить их вместе. Итак, еще раз мне нужно выполнить N (N + 1) / 4 сложения. Сложив их вместе, мы оставляем N^2 в качестве доминирующего термина. Так будет ли большой O этого алгоритма O(N^2)? Или я что-то не так делаю. Кажется странным иметь двоичную рекурсию и не иметь 2^n или log n в окончательном ответе

Answer 1

Есть на самом деле 2^n а также log n условия в конечном результате... вроде.

Для каждого вызова подмассива длины n для обеих половин этого массива выполняются два рекурсивных вызова плюс постоянный объем работы (оператор if, сложение, добавление в стек вызовов и т. д.). Таким образом, рекуррентное соотношение определяется как:

На данный момент мы можем просто использовать теорему мастера, чтобы непосредственно прийти к конечному результату - O(n), Но давайте вместо этого выведем это повторным расширением:

Условие остановки n = 1 дает максимальное значение m (игнорируя округление):

На шаге (*) мы использовали стандартную формулу для геометрических рядов. Так что, как вы видите, ответ включает в себя log n а также 2^n термины в некотором смысле, но они "отменяют", чтобы дать простой линейный член, который такой же, как и для простого цикла.