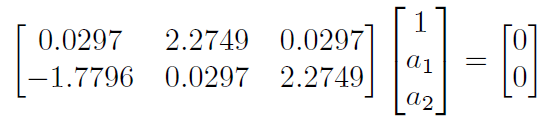Решение системы уравнений на MATLAB, когда константа существует в переменной матрице?

Question

Как мне решить следующую систему уравнений на MATLAB, когда один из элементов переменного вектора является константой? Пожалуйста, дайте код, если это возможно.

В более общем смысле, если решение заключается в использовании символической математики, как я буду генерировать большое количество переменных, скажем, 12 (а не только две), даже до их решения?

Answer 1

Например, создайте ряд символических переменных, используя syms, а затем составьте систему уравнений, как показано ниже.

syms a1 a2

A = [matrix]
x = [1;a1;a2];
y = [1;0;0];

eqs = A*x == y

sol = solve(eqs,[a1, a2])

sol.a1
sol.a2

---

Если у вас есть система с множеством переменных, вы можете определить все символы, используя syms и решить это, как указано выше.

Вы также можете выполнить оптимизацию параметров с fminsearch, Сначала вы должны определить функцию стоимости в отдельном файле функций, в этом примере она называется cost_fcn.m,

function J = cost_fcn(p)

    % make sure p is a vector
    p = reshape(p, [length(p) 1]);

    % system of equations, can be linear or nonlinear
    A = magic(12); % your system, I took some arbitrary matrix
    sol = A*p;

    % the goal of the system of equations to reach, can be zero, or some other
    % vector
    goal = zeros(12,1);

    % calculate the error
    error = goal - sol;

    % Use a cost criterion, e.g. sum of squares
    J = sum(error.^2);

end

Эта функция стоимости будет содержать вашу систему уравнений и решение задачи. Это может быть любая система. Вектор p будет содержать оцениваемые параметры, которые будут оптимизированы, начиная с некоторого начального предположения. Для оптимизации вам нужно будет создать скрипт:

% initial guess, can be zeros, or some other starting point
p0 = zeros(12,1);

% do the parameter optimization
p = fminsearch(@cost_fcn, p0);

В этом случае p0 это исходное предположение, которое вы предоставляете fminsearch, Затем значения этого начального предположения будут увеличиваться до тех пор, пока не будет найден минимум для функции стоимости. Когда оптимизация параметров закончена, p будет содержать параметры, которые приведут к наименьшей ошибке для вашей системы уравнений. Однако возможно, что это локальный минимум, если нет точного решения проблемы.

Answer 2

Ваша система чрезмерно ограничена, то есть у вас больше уравнений, чем неизвестных, поэтому вы не можете ее решить. Что вы можете сделать, это найти решение наименьших квадратов, используя mldivide, Сначала переставьте уравнения так, чтобы у вас были все постоянные члены справа от знака равенства, затем используйте mldivide:

>> A = [0.0297 -1.7796; 2.2749 0.0297; 0.0297 2.2749]
A =

   0.029700  -1.779600
   2.274900   0.029700
   0.029700   2.274900

>> b = [1-2.2749; -0.0297; 1.7796]
b =

  -1.274900
  -0.029700
   1.779600

>> A\b
ans =

  -0.022191
   0.757299