R: способ получить выражение модели, которая соответствует данным

Question

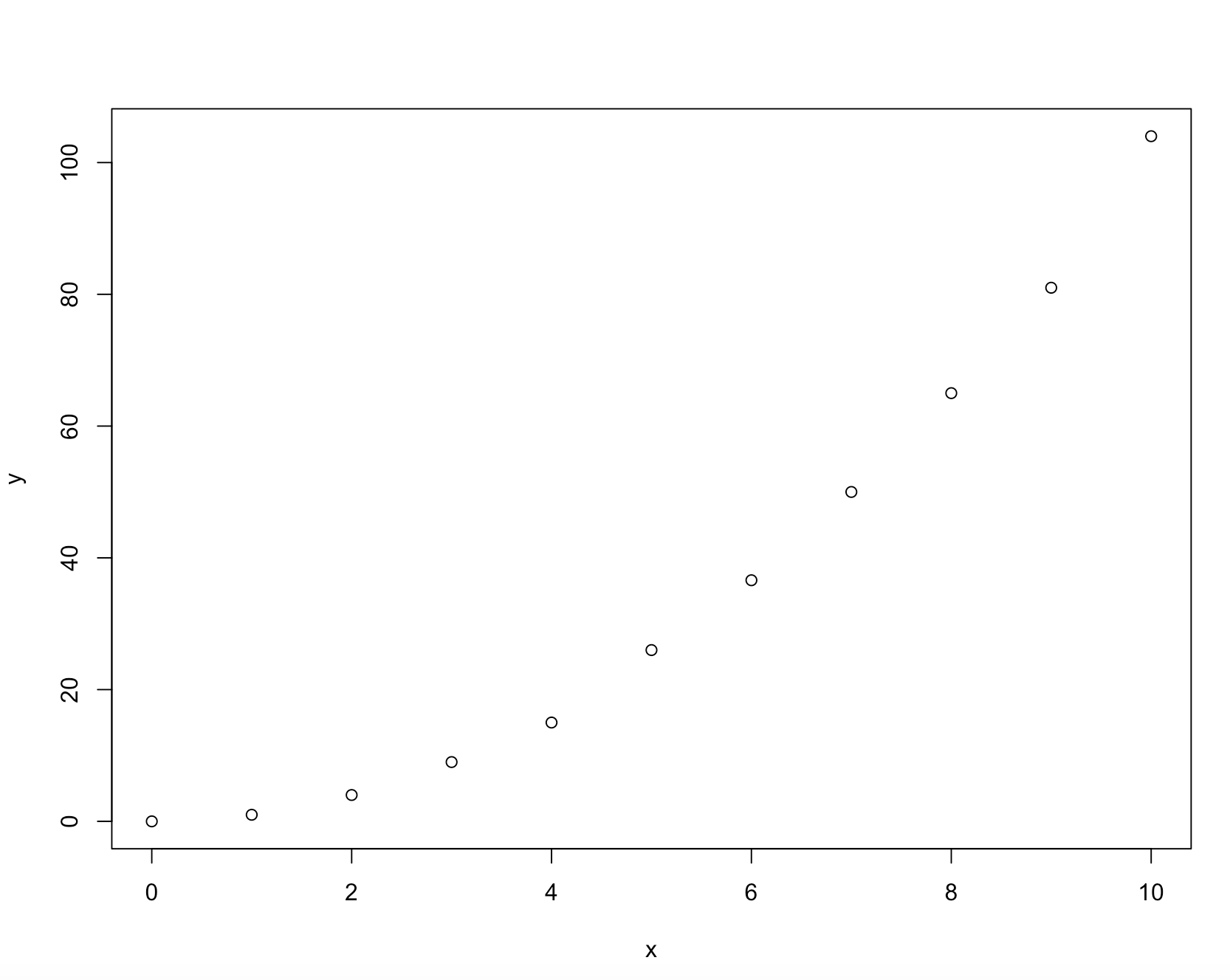
x = c(0:10)
y = c(0, 1, 4, 9, 15, 26, 36.6, 50, 65, 81, 104)
plot(y ~ x)

Предположим, у меня есть очень простой набор данных с 10 точками. Я пытаюсь придумать математическое уравнение для модели, которая описывает этот набор данных. В R есть разные методы сглаживания, такие как loess а также smooth.splineи т. д., которые делают хорошую работу по подгонке кривой к данным. У меня вопрос, есть ли способ в R получить формулу для этого соответствия? Т.е. для этого игрушечного набора данных довольно ясно видеть, что y = x^2 будет отличным выбором для этого набора данных.

Для более сложного набора данных, есть ли способ получить математическое выражение для кривой лесса, которая подходит для данных?

Answer 1

Похоже, у вас есть распределение, которое мы могли бы смоделировать с помощью этого типа степенной функции: y = a * b^(x). Предположим, что нелинейной регрессии не существует, мы можем решить эту проблему с помощью "линейной регрессии", которая, вероятно, использует метод наименьших квадратов. Нам просто нужно преобразовать оси путем вычисления логарифма обеих сторон уравнения. Опять же, мы просто не знаем "а" и "б".

ln (y) = ln [a * b ^ (x)] # Я использую натуральный логарифм (основание e).

ln (y) = ln (a) + ln (b ^ x)

ln (y) = [ln (b)] * (x) + ln (a) <------> Y = m (X) + B, где m = наклон, а B = вертикальный перехват. Я использовал заглавную B, чтобы мы не запутались.

Вам это сейчас кажется линейным уравнением? Итак, теперь мы преобразуем ось y в log_e(y), получаем статистику линейной регрессии, поднимаем "m" и "B" над основанием нашего логарифма, который равен e.

так е ^[ln(b)] дает нам "б", и...

е ^ [лн (а) дает нам,

и тогда мы знаем, что у = а * б ^ (х) численно.

Давайте посчитаем это. Я собираюсь устранить 0 в "х" и "у". Мы потеряем некоторую точность, но, как вы знаете, ln(0) = -infinity. Мы не можем этого иметь.

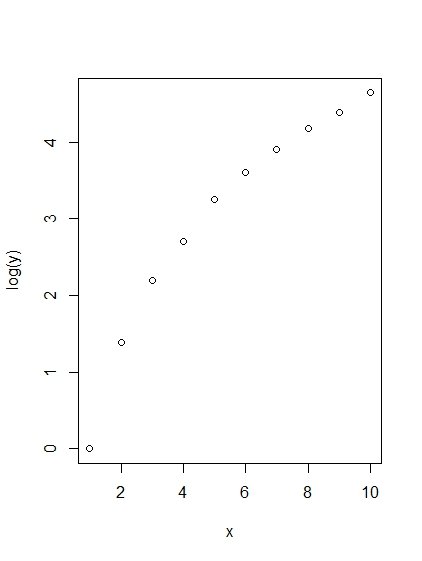
х <- 1:10

y <- c (1, 4, 9, 15, 26, 36,6, 50, 65, 81, 104)

Теперь было бы неплохо проверить, чтобы у нас было одинаковое количество сингулярных переменных в "x" и "y", иначе мы не сможем построить график точек.

длина (х) == длина (у) 1 ИСТИНА

И у "х" 10 терминов, и у "у" 10 терминов.

plot (y ~ x) # Посмотрим, как выглядит график. Ты уже знаешь.

Теперь преобразовать это?

сюжет (лог (у) ~ х))

Хм, это не похоже на прямую линию после трансформации.

Следовательно, это не степенная функция. Я был неправ. Опять же, этот журнал является основой е.

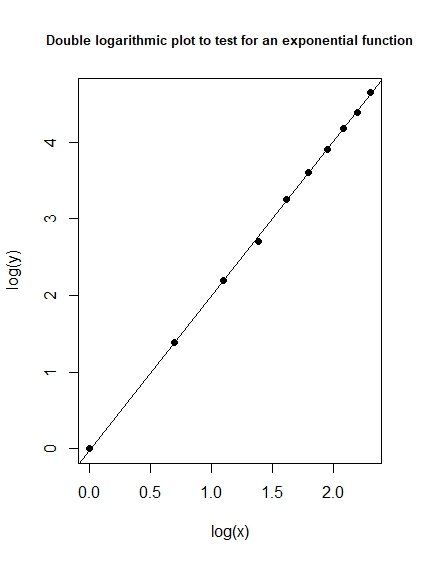
Давайте попробуем двойной логарифмический график.

plot (log (y) ~ log (x), main = "Двойной логарифмический график для проверки экспоненциальной функции", pch = 16, cex.main = 0.8)

Это прямая линия, поэтому мы находимся в чистоте. Я был неправ по поводу распределения мощности. Эта экспоненциальная функция подходит для случая, когда...

у = а * х ^ (б), который при вычислении логарифма обеих сторон уравнения, вы получите.

ln (y) = b [ln (x)] + ln (a)

так тогда: e^[ln(a)], где ln (a) - вертикальная точка пересечения, = "a"

тогда: b[ln(x)] или логарифмически скорректированный наклон. У нас уже есть "е", не нужно его настраивать.

модель <- lm (log (y) ~ log (x))

abline (модель)

Резюме (модель)

Вызов: lm(формула = log(y) ~ log(x))

Остатки: мин 1 квартал, медиана 3 кв, максимум -0,069478 -0,000490 0,005266 0,012249 0,031271

Коэффициенты: Оценка Станд. Значение ошибки t Pr (> | t |)
(Перехват) -0,01376 0,02212 -0,622 0,551

log (x) 2,01349 0,01330 151,360 4,06e-15 ***

Signif. коды: 0 '' 0,001 '' 0,01 '' 0,05 '.' 0,1 '' 1

Остаточная стандартная ошибка: 0,02925 на 8 степенях свободы Множественный R-квадрат: 0,9997, Скорректированный R-квадрат: 0,9996 F-статистика: 2,291e+04 на 1 и 8 DF, значение p: 4,06e-15

тогда в нашей функции y = a * x^(b), чтобы получить "a", мы вычисляем...

опыт (-0,01376) 1 0,9863342

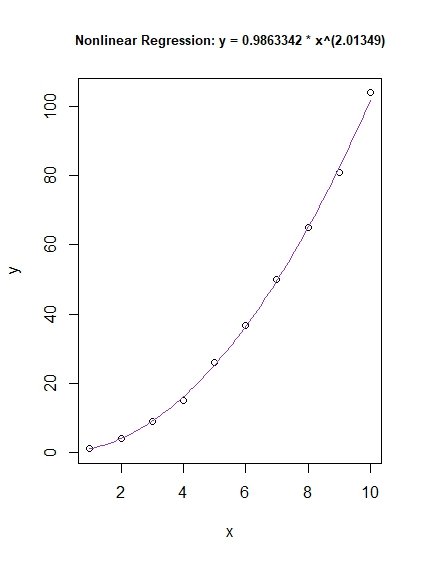
plot (y ~ x, main = "Нелинейная регрессия: y = 0.9863342 * x^(2.01349)", cex.main = 0.8)

Теперь, не просто доверяй мне, пока не подберёшься для кривой.

кривая (0,9863342 * x ^ (2,01349), col = "darkorchid3", add = TRUE)

Итак, мы наконец-то посчитали, что...

y = a * x^(b) <----------> y = 0,9863342 * x ^ (2,01349), поэтому a = 0,9863342 и b = 2,01349

Технически я не делал ни нелинейной регрессии, ни итерационных догадок. Чтобы дать вам статистически корректный ответ, я должен сказать вам, что есть некоторые стандартные ошибки линейной регрессии наименьших квадратов, и ошибки, каким-то образом скорректированные, когда я вычислил e^(-0.01376). Но я отлично подхожу.