Как получить отрезок прямоугольника пересечения линии в Matlab

Question

Я хочу найти весовую матрицу для метода алгебраической реконструкции. Для этого мне нужно найти пересечение линии с сеткой. я могу найти прямое пересечение линии с линией, но я должен хранить номер сетки пересеченного отрезка линии в зависимости от номера. поэтому предположим, что если первый квадрат сетки не пересекается с сеткой, тогда положим ноль в первый элемент весовой матрицы. вот код, который я пробовал для пересечения линии:

ak = 3:6
aka = 3:6
x = zeros(size(aka))
y = zeros(size(ak))
for k = 1:length(ak)
  line([ak(1) ak(end)], [aka(k) aka(k)],'color','r')
end

% Vertical grid
for k = 1:length(aka)
  line([ak(k) ak(k)], [aka(1) aka(end)],'color','r')
end
hold on;
 X =[0 15.5]
 Y = [2.5 8.5] 
 m = (Y(2)-Y(1))/(X(2)-X(1)) ;
 c = 2.5 ; 
 plot(X,Y)
axis([0 10 0 10])
axis square
% plotting y intercept
for i = 1:4
    y(i) = m * ak(i) + c
    if y(i)<2 || y(i)>6
        y(i) = 0
    end
end
% plotting x intercept
for i = 1:4
   x(i) = (y(i) - c)/m 
    if x(i)<2 || x(i)>6
        x(i) = 0
    end
end  
z = [x' y']

Объяснение проблемы:

У меня есть строка, определяемая параметрами m, h, где y = m*x + h Эта линия проходит через сетку (то есть пиксели). За каждый квадрат (a, b) сетки (то есть квадрат [a, a+1]x[b, b+1]), Я хочу определить, пересекает ли данная линия этот квадрат или нет, и если да, то какова длина сегмента в квадрате. Так что я могу построить матрицу весов, которая необходима для метода алгебраической реконструкции.

Answer 1

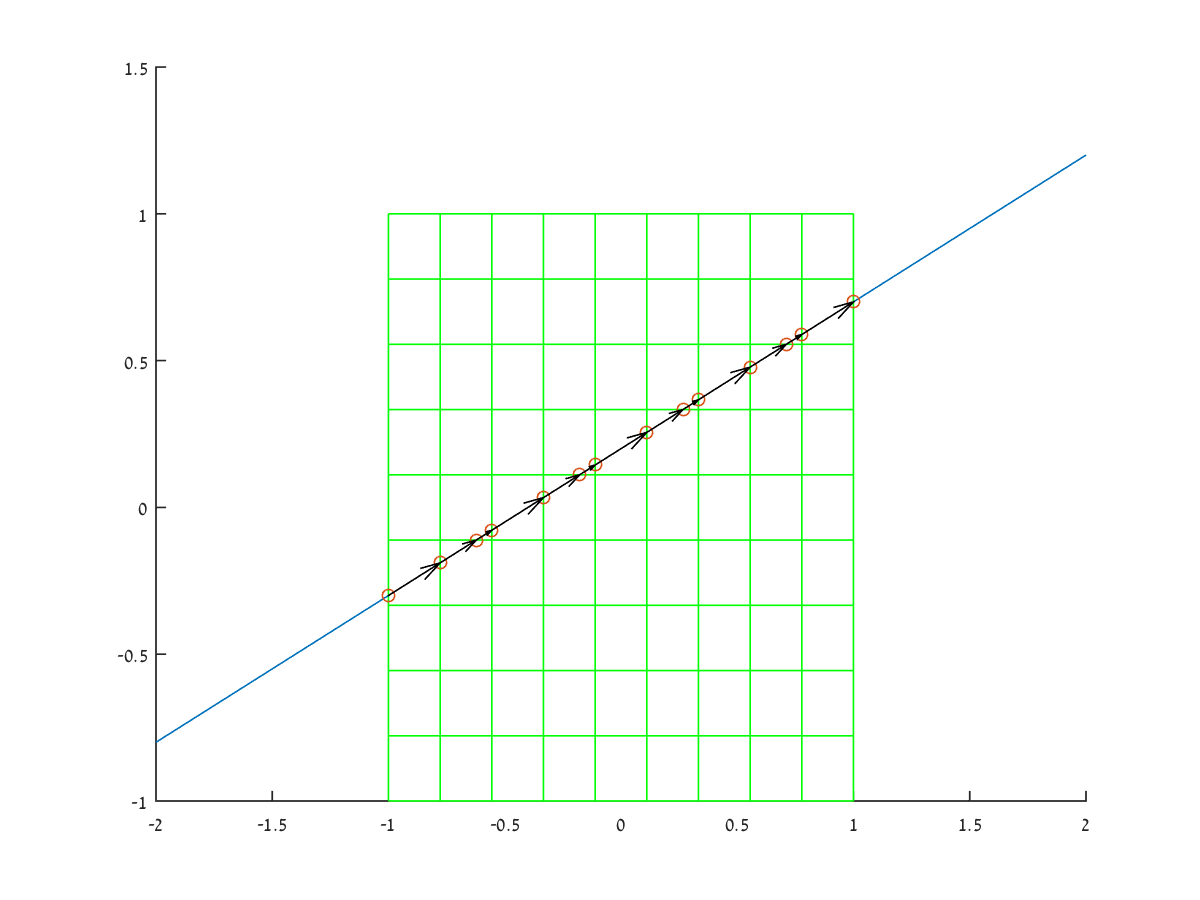
Вот хороший способ пересечь линию с сеткой прямоугольников и получить длины каждого из сегментов пересечения: я использовал пересечение линии линии из псевдокода в третьем ответе по этой ссылке

% create some line form the equation y=mx+h
m = 0.5; h = 0.2;
x = -2:0.01:2;
y = m*x+h;
% create a grid on the range [-1,1]
[X,Y] = meshgrid(linspace(-1,1,10),linspace(-1,1,10));
% create a quad mesh on this range
fvc = surf2patch(X,Y,zeros(size(X)));
% extract topology
v = fvc.vertices(:,[1,2]);
f = fvc.faces;
% plot the grid and the line
patch(fvc,'EdgeColor','g','FaceColor','w'); hold on;
plot(x,y);
% use line line intersection from the link
DC = [f(:,[1,2]);f(:,[2,3]);f(:,[3,4]);f(:,[4,1])];
D = v(DC(:,1),:);
C = v(DC(:,2),:);
A = repmat([x(1),y(1)],size(DC,1),1);
B = repmat([x(end),y(end)],size(DC,1),1);
E = A-B;
F = D-C;
P = [-E(:,2),E(:,1)];
h = dot(A-C,P,2)./dot(F,P,2);
% calc intersections
idx = (0<=h & h<=1);
intersections = C(idx,:)+F(idx,:).*repmat(h(idx),1,2);
intersections = uniquetol(intersections,1e-8,'ByRows',true);
% sort by x axis values
[~,ii] = sort(intersections(:,1));
intersections = intersections(ii,:);
scatter(intersections(:,1),intersections(:,2));
% get segments lengths
directions = diff(intersections);
lengths = sqrt(sum(directions.^2,2));
directions = directions./repmat(sqrt(sum(directions.^2,2)),1,2);
directions = directions.*repmat(lengths,1,2);
quiver(intersections(1:end-1,1),intersections(1:end-1,2),directions(:,1),directions(:,2),'AutoScale','off','Color','k');

Это результат (длина стрелок на изображении равна длине сегмента)