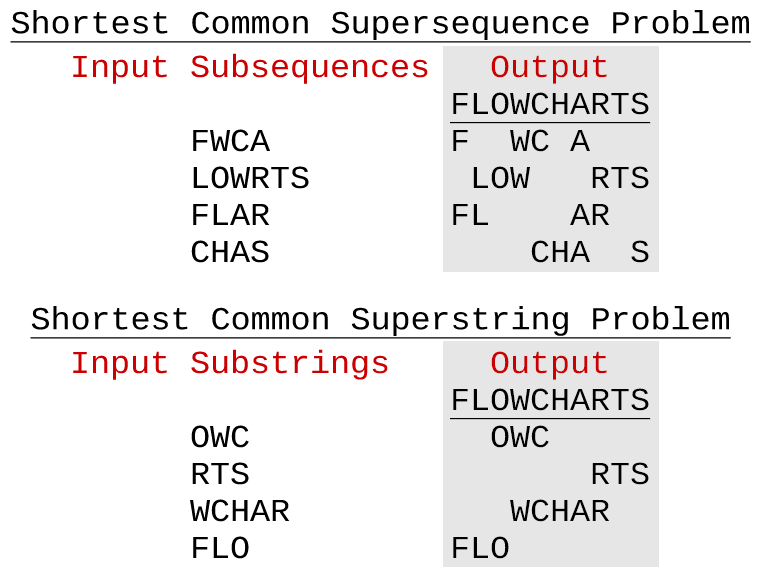
Найти суперпоследовательность заданных упорядоченных подпоследовательностей в Java
Я столкнулся с этой проблемой в несвязанной программе, которую я пишу, и я потратил довольно много часов, пытаясь решить ее, потому что я думал, что это будет весело. Это было, но я не мог сделать это полностью. Мой код только решает последовательность некоторых подмножеств. Эта проблема также напоминает общую математическую задачу, которая, вероятно, решалась различными способами в течение десятилетий, но мне не хватает математических навыков и терминологии, чтобы найти решение или вообще что-то об этой конкретной проблеме в Интернете.
У меня есть набор подпоследовательностей, которые, как я знаю, являются частью большой, неизвестной (супер?) Последовательности. Я не думаю, что эти подпоследовательности являются наборами в математическом смысле, потому что они упорядочены, но они похожи в том, что они не содержат повторяющихся элементов. То же самое касается мастера / супер /whateversequence. (Для ясности я буду называть это суперпоследовательностью.)
Все подпоследовательности содержат данные одного и того же типа, однако данные не упорядочены в алфавитном порядке, в порядке возрастания или чего-либо подобного. В некотором смысле данные находятся в произвольном порядке: в суперпоследовательности. И это то, что меня интересует. Я хочу найти неизвестную суперпоследовательность этих подпоследовательностей.
Для простоты я попытался решить эту проблему, используя буквы алфавита, но позже я смогу реорганизовать код в соответствии со своими потребностями. Очевидно, потому что я все еще пытаюсь решить эту проблему, я начал с подходящего слова для суперпоследовательности, которое не содержит повторяющихся элементов: FLOWCHARTS.
Затем я придумал следующие шесть подпоследовательностей:
F,W,C,R
L,H,A
L,O,H,A,R,S
C,S
R,T,S
F,O,W,H,A,S
Вот мой метод упорядочения последовательности:
// LinkedHashMappedKeyValueList keeps the data in the order it was inserted and allows one key to have multiple values.
private static LinkedHashSet<Character> orderSequence(final Set<Character> unorderedSequence, final LinkedHashMappedKeyValueList ruleMap)
{
List<Character> orderedSequence = new ArrayList<Character>(unorderedSequence);
// Order the sequence according to the rules.
System.out.println("---- ORDERING SEQUENCE ----");
for (Map.Entry<Character, LinkedHashSet<Character>> rule : ruleMap.entrySet())
{
char currentChar = rule.getKey();
LinkedHashSet<Character> ruleChars = rule.getValue();
System.out.println("Processing rule " + currentChar + "<" + ruleChars.toString());
if (orderedSequence.contains(currentChar))
{
int ruleCharIndex = -1;
int smallestRuleCharIndex = Integer.MAX_VALUE;
Iterator<Character> it = ruleChars.iterator();
// Find the rule character with the smallest index.
while (it.hasNext())
{
char ruleChar = it.next();
ruleCharIndex = orderedSequence.indexOf(ruleChar);
System.out.println("\tChecking for rule character: " + ruleChar + " (" + ruleCharIndex + ")");
if (ruleCharIndex > -1 && smallestRuleCharIndex > ruleCharIndex)
smallestRuleCharIndex = ruleCharIndex;
}
if (smallestRuleCharIndex != Integer.MAX_VALUE)
System.out.println("\tMoving '" + currentChar + "' before '"
+ orderedSequence.get(smallestRuleCharIndex) + "'.");
else
System.out.println("\tMoving '" + currentChar + "' to the end of the sequence.");
if (!moveBefore(orderedSequence.indexOf(currentChar), smallestRuleCharIndex, orderedSequence))
System.out.println("\tAlready in correct position.");
else
System.out.println("\tCurrent sequence: " + listToString(orderedSequence));
}
else
throw new ArithmeticException("Element of a subsequence not a part of the sequence.");
}
return new LinkedHashSet<Character>(orderedSequence);
}
В конце концов мой код нашел супер-последовательность F,L,O,W,H,C,A,R,T,S для этих подпоследовательностей, что довольно близко, но не идеально. Мне также нужно запустить мой метод заказа несколько раз, чтобы придуманный мной "алгоритм" тоже не был идеальным. "Карта правил" - это хэш-карта, в которой ключом является другая хэш-карта объектов Character, которые идут после ключевого символа в подпоследовательностях (и, следовательно, в суперпоследовательности).
Есть ли какая-нибудь библиотека Java, которую я мог бы использовать для поиска последовательности? Может ли кто-то указать мне правильное направление, говоря мне, как это называется, и / или помогая мне найти правильные алгоритмы для работы?
Кроме того, сокращенный вывод консоли моей программы:
---- BUILDING RULE MAP ----
Subsequences: F,W,C,R
L,H,A
L,O,H,A,R,S
C,S
R,T,S
F,O,W,H,A,S
All subsequences processed. Number of ordering rules: 10
Rule map: (F<[W, O]),(W<[C, H]),(C<[R, S]),(R<[, S, T]),(L<[H, O]),(H<[A]),(A<[, R, S]),(O<[H, W]),(S<[]),(T<[S])
---- BUILDING UNORDERED SEQUENCE ----
Sequence size is 10.
Unordered sequence: F,W,C,R,L,H,A,O,S,T
---- ORDERING SEQUENCE ----
Processing rule F<[W, O]
Moving 'F' before 'W'.
Already in correct position.
Processing rule W<[C, H]
Moving 'W' before 'C'.
Already in correct position.
Processing rule C<[R, S]
Moving 'C' before 'R'.
Already in correct position.
Processing rule R<[, S, T]
Moving 'R' before 'S'.
Current sequence: F,W,C,L,H,A,O,R,S,T
Processing rule L<[H, O]
Moving 'L' before 'H'.
Already in correct position.
Processing rule H<[A]
Moving 'H' before 'A'.
Already in correct position.
Processing rule A<[, R, S]
Moving 'A' before 'R'.
Current sequence: F,W,C,L,H,O,A,R,S,T
Processing rule O<[H, W]
Moving 'O' before 'W'.
Current sequence: F,O,W,C,L,H,A,R,S,T
Processing rule S<[]
Moving 'S' to the end of the sequence.
Current sequence: F,O,W,C,L,H,A,R,T,S
Processing rule T<[S]
Moving 'T' before 'S'.
Already in correct position.
Previous sequence: F,W,C,R,L,H,A,O,S,T
Ordered sequence: F,O,W,C,L,H,A,R,T,S
Sequences match: false
---- ORDERING SEQUENCE ----
Processing rule F<[W, O]
Moving 'F' before 'O'.
Already in correct position.
Processing rule W<[C, H]
Moving 'W' before 'C'.
Already in correct position.
Processing rule C<[R, S]
Moving 'C' before 'R'.
Current sequence: F,O,W,L,H,A,C,R,T,S
Processing rule R<[, S, T]
Moving 'R' before 'T'.
Already in correct position.
Processing rule L<[H, O]
Moving 'L' before 'O'.
Current sequence: F,L,O,W,H,A,C,R,T,S
Processing rule H<[A]
Moving 'H' before 'A'.
Already in correct position.
Processing rule A<[, R, S]
Moving 'A' before 'R'.
Current sequence: F,L,O,W,H,C,A,R,T,S
Processing rule O<[H, W]
Moving 'O' before 'W'.
Already in correct position.
Processing rule S<[]
Moving 'S' to the end of the sequence.
Already in correct position.
Processing rule T<[S]
Moving 'T' before 'S'.
Already in correct position.
Previous sequence: F,O,W,C,L,H,A,R,T,S
Ordered sequence: F,L,O,W,H,C,A,R,T,S
Sequences match: false
---- ORDERING SEQUENCE ----
Processing rule F<[W, O]
Moving 'F' before 'O'.
Current sequence: L,F,O,W,H,C,A,R,T,S
Processing rule W<[C, H]
Moving 'W' before 'H'.
Already in correct position.
Processing rule C<[R, S]
Moving 'C' before 'R'.
Current sequence: L,F,O,W,H,A,C,R,T,S
Processing rule R<[, S, T]
Moving 'R' before 'T'.
Already in correct position.
Processing rule L<[H, O]
Moving 'L' before 'O'.
Current sequence: F,L,O,W,H,A,C,R,T,S
Processing rule H<[A]
Moving 'H' before 'A'.
Already in correct position.
Processing rule A<[, R, S]
Moving 'A' before 'R'.
Current sequence: F,L,O,W,H,C,A,R,T,S
Processing rule O<[H, W]
Moving 'O' before 'W'.
Already in correct position.
Processing rule S<[]
Moving 'S' to the end of the sequence.
Already in correct position.
Processing rule T<[S]
Moving 'T' before 'S'.
Already in correct position.
Previous sequence: F,L,O,W,H,C,A,R,T,S
Ordered sequence: F,L,O,W,H,C,A,R,T,S
Sequences match: true
Sequence ordered according to the limits of the rule map.
Sequence found after 2 tries.
Expected sequence: F,L,O,W,C,H,A,R,T,S FLOWCHARTS
Found sequence: F,L,O,W,H,C,A,R,T,S FLOWHCARTS
Sequences match: false
2 ответа
Проблема, которую я описываю в своем вопросе, является самой короткой общей проблемой суперпоследовательности. Я не искал это в Интернете, потому что при работе над кодом я был слишком сосредоточен на математических наборах, и только когда я начал писать свой вопрос, я понял, что работаю с последовательностями. На самом деле, я думал, что просто наговорил слово "супер-последовательность". Оказывается, это именно то слово, которое мне нужно было искать в Интернете, чтобы найти несколько страниц материалов, связанных с этой проблемой.
Комментарий Оливера Чарльзуорта абсолютно верен. В данных подпоследовательностях отсутствует информация для создания правильной суперпоследовательности, поэтому в моем примере нет способа найти действительную суперпоследовательность. Комментарий Коффи о биоинформатике, скорее всего, относится к самой короткой общей проблеме суперструн, которая имеет применение в реконструкции последовательностей ДНК, что-то обсуждается в этом вопросе. Задачи наименьшей общей суперпоследовательности и суперструн на первый взгляд очень похожи, однако, в задаче суперструн подстроки должны состоять из смежных элементов суперструны, в отличие от задачи суперпоследовательности. (Показано ниже.)
Обе проблемы также являются NP-полными или "NP-сложными". Насколько я понимаю, у этих проблем нет оптимального решения или какого-то волшебного алгоритма, который вы можете просто скопировать и вставить в свой код. Есть только аппроксимации и "достаточно хорошие" решения.
Удивительно, но мне не удалось найти полный Java-код, который приближает эту проблему, но я наткнулся на несколько сайтов с кодом на других языках. Ниже я перечислил некоторые полезные ресурсы, которые я нашел при исследовании этой проблемы. Я также включил ресурсы, связанные с самой короткой общей проблемой суперструн, как она связана.
Дополнительные ресурсы для дальнейшего изучения
- Google ученый
- Кратчайшая общая проблема суперпоследовательности Андреаса Вестлинга (с кодом C)
- Наука Direct документы по этому вопросу
- Документы на CiteSeerX
- Аппроксимационные алгоритмы для кратчайшей общей задачи суперструн Джонатана Тернера
- Связанные вопросы Stackru
- Розеттский код (разные языки)
- питон
- Java (проблема суперструн)
- Рубин (в заголовке написано суперструна, но мне кажется, что это проблема суперпоследовательности.)
То, что вы просите - это рассчитать общий заказ по частичному заказу. Я не мог найти много работы по этому вопросу. Однако мы можем немного обсудить эту проблему здесь.
Рассматривать A<B<C<D, Если у нас есть последовательности A<C, B<D а также C<DМы никогда не сможем рассчитать общий заказ. Мы только получаем A<C<D а также B<D,
Я думаю, что можно доказать, что нам понадобятся все N-1 отношения формы X<Y с X а также Y последовательно представлять в последней цепочке, чтобы восстановить общий заказ (могут быть дополнительные, но это дополнительная информация). В качестве не строгой демонстрации, предположим, что мы имеем A1<A2<A3<...<AN и предположим, что мы можем восстановить из частичных заказов A_begin в A_end, Теперь, чтобы поместить это в правильное положение в общем порядке, нам нужно знать, что A_(begin-1)<A_begin, Нет другого отношения, которое позволит ему вписаться в общий порядок. Продолжая это вниз в A_begin..A_end мы должны быть в состоянии показать какой-то индукцией / бесконечным спуском, что нам понадобятся все отношения, заданные последовательными символами слова, чтобы восстановить его.
Информация, отсутствующая в приведенном выше наборе последовательностей: F<L а также C<H, Последовательности, которые могут быть получены W->C->R->T->S, F->O->W->H->A->R->T->S а также L->O->W->H->A->R->T->S, Для расчета остатка требуется больше информации.
В приведенном выше случае после разложения и устранения дублирования имеем следующие соотношения:
A,R
A,S <-- redundant since R<S and A<R
C,R
C,S <-- redundant since R<S and A<R
F,O
F,W <-- redundant since O<W and F<O
H,A
L,H <-- redundant since O<H and L<O
L,O
O,H <-- redundant since O<W and W<H
O,W
R,S <-- redundant since T<S and R<T
R,T
T,S
W,C
W,H
Существует 16 отношений, из которых 6 сразу избыточны. Устраняя избыточности мы получаем следующие 10 соотношений:
A,R <-- consecutive letters in actual word
C,R
F,O
H,A <-- consecutive letters in actual word
L,O <-- consecutive letters in actual word
O,W <-- consecutive letters in actual word
R,T <-- consecutive letters in actual word
T,S <-- consecutive letters in actual word
W,C <-- consecutive letters in actual word
W,H
Единственные, отсутствующие в оригинальной последовательности: F<L а также C<H, Дополнительные данные отношения C<R, F<O а также W,H повторили LHS или RHS и предоставили неактивную информацию (в основном они связывают две частично упорядоченные цепочки, но не в конечных точках, поэтому вы знаете, что цепочка должна быть объединена или меньше другой, но не знаете, где).
Есть несколько способов реализовать это после добавления отсутствующих отношений. Ваш код может работать сам по себе.