Возьмите каждый k-й элемент из ряда (1 .. n) натуральных чисел
Например, у нас есть серии 1, 2, 3, 4, 5. Мы берем каждые 3 элемента => 3, 1, 5, 2, 4 (выбранный элемент не должен оставаться, мы можем взять, пока серия не пуста). Наивная реализация по кругу двусвязного списка не является хорошей идеей, причиной производительности. Можете ли вы дать мне совет, какие структуры данных и алгоритмы более применимы?
4 ответа
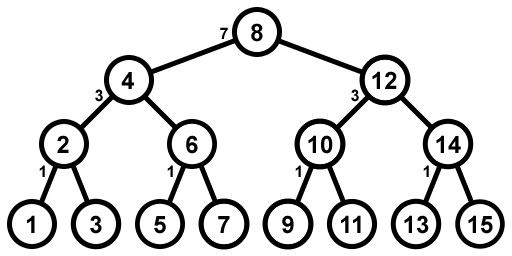
Создайте полное двоичное дерево, содержащее числа от 1 до n, например, для n=15, которое будет:
В каждой ветви сохраните количество узлов слева от него; это позволит нам быстро найти i-й узел. (Вы увидите, что это дерево имеет очень предсказуемую структуру и значения, и его генерация гораздо эффективнее, чем построение бинарного дерева одинакового размера со случайно упорядоченными значениями. Это также идеальный кандидат для дерева в ан массив).
Затем, чтобы найти i-ое число, начните с корневого узла, и на каждом узле, если i на единицу больше, чем число узлов слева, вы нашли i-ое число, иначе идите налево (если я не больше, чем количество узлов слева) или справа (если я больше, чем на 1 больше, чем количество узлов слева).
Всякий раз, когда вы идете налево, уменьшайте количество узлов слева от этого узла (потому что мы удалим один).
Всякий раз, когда вы идете направо, уменьшайте искомое число на число узлов слева от узла, плюс 1 (или плюс 0, если значение в узле было стерто).
Когда вы нашли i-й узел, прочитайте его значение (чтобы добавить в список порядка удаления), а затем установите его значение равным 0. После этого, если i-й узел, который мы ищем, имеет значение, стертое, мы пойдем направо и затем возьмем самый левый узел.
Мы начинаем со значения i = k, а затем каждый раз, когда стираем число в i-м узле, уменьшаем общее количество узлов и устанавливаем i = (i + k - 1) % total (или если это ноль: i = total).
Это дает log 2 N времени поиска и общую сложность N×LogN.
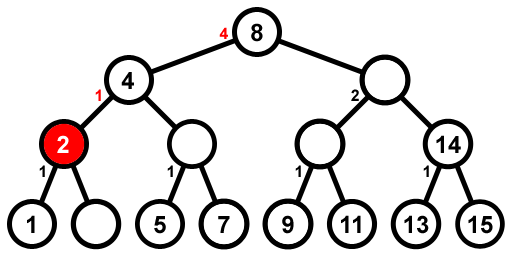
Пример прохождения: с n=15 (как на рисунке выше) и k = 6, первые шаги 6, 12, 3, 10, 2. На этом этапе ситуация:
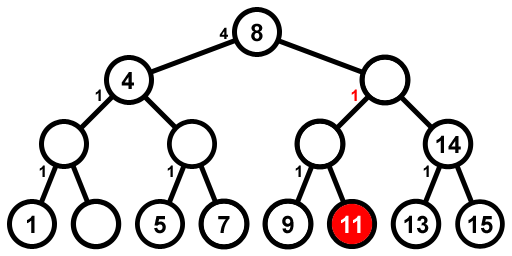
Мы только что удалили второй номер, и теперь i = 2 + 6 - 1 = 7, Мы начинаем с корневого узла, который имеет 4 узла слева от него и все еще имеет свое значение, поэтому мы идем направо и вычитаем 5 из 7, которые мы ищем, и получаем 2. Мы приходим к узлу 12 (который был стереть) и найдите 2 узла слева от него, поэтому мы уменьшаем количество узлов слева от него и затем идем налево. Мы подходим к узлу 10 (который был удален) и обнаруживаем, что он имеет 1 узел слева от него, и 1 = 2 - 1, так что это тот узел, который мы ищем; однако, так как его значение было стерто, мы идем направо и вычитаем 1 из 2, которое мы ищем, и получаем 1. Мы достигаем узла 11, который имеет 0 узлов слева от него (потому что это лист), и 0 = 1 - 1, так что это узел, который мы ищем.
Затем мы уменьшаем общее количество узлов с 10 до 9 и обновляем i с 7 до (7 + 6 - 1) % 9 = 3 и продолжайте, чтобы найти третий узел (который теперь является со значением 5).
Вот простая реализация в JavaScript. Он решает серию из 100000 чисел менее чем за секунду, и, вероятно, его можно было бы сделать быстрее и эффективнее с помощью структуры "дерево в массиве".
(В отличие от приведенного выше объяснения, индексы чисел начинаются с нуля, чтобы упростить код; таким образом, индекс 0 - это первое число в дереве, и мы ищем узел с числом дочерних элементов, связанных слева, которые равны целевой индекс.)
function Tree(size) { // CONSTRUCTOR
var height = Math.floor(Math.log(size) / Math.log(2));
this.root = addNode(height, 1 << height, size);
this.size = size;
function addNode(height, value, max) { // RECURSIVE TREE-BUILDER
var node = {value: value > max ? 0 : value, lower: (1 << height) - 1};
if (height--) {
node.left = addNode(height, value - (1 << height), max);
if (value < max) { // DON'T ADD UNNECESSARY RIGHT NODES
node.right = addNode(height, value + (1 << height), max);
}
}
return node;
}
}
Tree.prototype.cut = function(step) { // SEE ANSWER FOR DETAILS
var sequence = [], index = (step - 1) % this.size;
while (this.size) {
var node = this.root, target = index;
while (node.lower != target || node.value == 0) {
if (target < node.lower) {
--node.lower;
node = node.left;
} else {
target -= node.lower + (node.value ? 1 : 0);
node = node.right;
}
}
sequence.push(node.value);
node.value = 0;
index = (index + step - 1) % --this.size;
}
return sequence;
}
var tree = new Tree(15);
var sequence = tree.cut(6);
document.write("15/6→" + sequence + "<BR>");
tree = new Tree(100000);
sequence = tree.cut(123456);
document.write("100000/123456→" + sequence);НОТА:
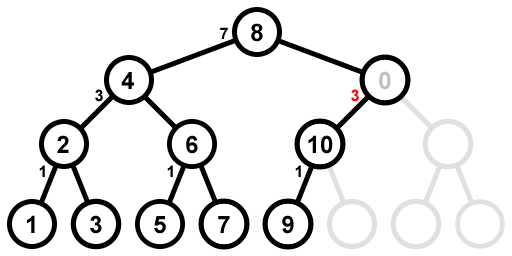
Если вы посмотрите на дерево для n=10, то увидите, что узел справа от корня имеет неполное дерево с двумя узлами слева, но алгоритм, реализованный в приведенном выше примере кода, дает неверный левый угол. Количество узлов 3 вместо 2:
Однако узлы с неполным деревом слева никогда не содержат значения сами и никогда не имеют узлов справа. Таким образом, вы все равно всегда идете налево, и тот факт, что число их левых узлов слишком велико, не имеет значения.
Если вам просто нужно последнее число, оно известно как проблема Иосифа, и есть хорошо известные формулы для вычисления ответа в O(N) время.
Я не знаю, можно ли адаптировать его для запуска полной симуляции, поэтому я опишу простой O(N log N) Решение здесь:
Будем хранить все числа в трепе с неявными ключами. Нам нужно найти k-ый элемент и удаляйте его на каждом шаге (на самом деле, может быть сдвиг, так что это больше похоже на (cur_shift + k) % cur_size, но это на самом деле не имеет значения). Трепа может это сделать. Нам просто нужно разделить его на 3 части [0, k - 1], [k, k] а также [k + 1, cur_size - 1]напечатайте число в узле, которое соответствует второй части, и объедините первую и последнюю части вместе. Это требует O(log N) время на шаг, поэтому оно должно быть достаточно для заданных ограничений.
Вот реализация с представлением в виде массива двоичного дерева, в котором в качестве значения узла хранится только размер левого поддерева. Входной массив на самом деле не хранится, но предполагается, что он скрытым образом находится на нижнем уровне, ниже двоичного дерева:
function josephusPermutation(size, step) {
var len = 1 << 32 - Math.clz32(size-1), // Smallest power of 2 >= size
tree = Array(len).fill(0), // Create tree in array representation
current = 0,
skip = step - 1,
result = Array(size).fill(0),
goRight, leftSize, order, i, j;
// Initialise tree with sizes of left subtrees as node values
(function init(i) {
if (i >= len) return +(i - len < size); // Only count when within size
var left = tree[i] = init(i*2); // recursive, only store left-size
return left + (left ? init(i*2+1) : 0); // return sum of left and right
})(1);
for (j = 0; j < result.length; j++, size--) {
current = (current + skip) % size; // keep within range
order = current;
for (i = 1; i < len; i = i*2+goRight) {
leftSize = tree[i];
goRight = order >= leftSize;
if (goRight) {
order -= leftSize; // Moving rightward, counting what is at left side.
} else {
tree[i]--; // we will remove value at left side
}
}
result[j] = 1 + i - len;
}
return result;
}
var sequence = josephusPermutation(100000, 123456);
console.log(sequence.join(','));Ниже приведена реализация Лэй Вана и Сяодун Вана (2013) 1 O(n log k) алгоритм (очень похож на алгоритм Эррола Ллойда, опубликованный в 1983 г., если не основан на нем). Идея состоит в том, чтобы разделить оригинальную последовательность на n/m бинарные деревья высоты log k, Алгоритм на самом деле разработан для "кошачьей" проблемы Джозефуса, где участники могут иметь более одной жизни (перечислены в переменной массива ниже, global.l).
Мне тоже нравится O(1) космические алгоритмы Кнута, Аренса и Капланского (изложенные в магистерской диссертации Грегори Уилсона, Калифорнийский государственный университет, Хейворд, 1979 г. 2), которые занимают больше времени, хотя могут быть довольно быстрыми в зависимости от параметров.
Алгоритм Кнута для J(n,d,t) (t это ith хит), по убыванию:
Let x1 = d * t and for k = 2,3,...,
let x_k = ⌊(d * x_(k−1) − d * n − 1) / (d − 1)⌋
Then J(n,d,t) = x_p where x_p is the first term in the sequence <= n.
Алгоритм Аренса для J(n,d,t) Восходящая последовательность:
Let a1 = 1 and for k = 2,3,...
let a_k = ⌈(n − t + a_(k−1)) * d / (d − 1)⌉
If a_r is the first term in the sequence such that a_r + 1 ≥ d * t + 1
then J(n,d,t) = d * t + 1 − a_r.
Алгоритм Капланского для J(n,d,t):
Let Z+ be the set of positive integers and for k =1,2,...,t
define a mapping P_k : Z+ → Z+ by P_k(m) = (m+d−1)−(n−k+1)(m−k+d−1)/(n−k+1)
Then, J(n,d,t) = P1 ◦ P2 ◦···◦Pt(t).
Код JavaScript:
var global = {
n: 100000,
k: 123456,
l: new Array(5).fill(1),
m: null,
b: null,
a: [],
next: [],
prev: [],
i: 0,
limit: 5,
r: null,
t: null
}
function init(params){
global.m = Math.pow(2, Math.ceil(Math.log2(params.k)));
params.b = Math.ceil(params.n / global.m);
for (let i=0; i<params.b; i++){
let s = i * global.m,
t = (i + 1) * global.m,
u = [];
for (let j=0; j<global.m; j++)
u[j] = 0;
for (let j=s; j<=Math.min(t-1,params.n-1); j++)
u[j-s] = -(j + 1);
global.a[i] = [];
build(u, global.a[i]);
t = (i + 1) % params.b;
params.next[i] = t;
params.prev[t] = i;
}
}
function build(u,v){
function count(_v, i){
if (global.m < i + 2){
if (_v[i] < 0)
return 1;
else
return 0;
} else {
_v[i] = count(_v, 2*i + 1);
_v[i] = _v[i] + count(_v, 2*i + 2);
return _v[i];
}
}
for (let i=0; i<global.m; i++)
v[global.m + i - 1] = u[i];
count(v, 0);
}
function algorithmL(n, b){
global.r = 0;
global.t = b - 1;
while (global.i < global.limit){
tree(global, global);
let j = leaf(global, global);
hit(global.i,j,global,global);
global.i = global.i + 1;
}
}
function tree(params_r,params_t){
if (params_t.t === global.next[params_t.t] && params_r.r < global.k){
params_r.r = global.k + global.a[params_t.t][0] - 1 - (global.k - params_r.r - 1) % global.a[params_t.t][0];
} else {
while (params_r.r < global.k){
params_t.t = global.next[params_t.t];
params_r.r = params_r.r + global.a[params_t.t][0];
}
}
}
function size(t,j){
if (global.a[t][j] < 0)
return 1
return global.a[t][j];
}
function leaf(params_r,params_t){
let j = 0,
nxt = params_r.r - global.k;
while (j + 1 < global.m){
let rs = size(params_t.t, 2*j + 2);
if (params_r.r - rs < global.k){
j = 2*j + 2;
} else {
j = 2*j + 1;
params_r.r = params_r.r - rs;
}
}
params_r.r = nxt;
return j;
}
function hit(i,j,params_r,params_t){
let h = -global.a[params_t.t][j];
console.log(h);
if (global.l[h-1] > 1)
global.l[h-1] = global.l[h-1] - 1;
else
kill(i,j,params_r,params_t);
}
function kill(i,j,params_r,params_t){
global.a[params_t.t][j] = 0;
while (j > 0){
j = Math.floor((j - 1) / 2);
global.a[params_t.t][j] = global.a[params_t.t][j] - 1;
}
if (params_t.t !== global.next[params_t.t]){
if (global.a[params_t.t][0] + global.a[global.next[params_t.t]][0] === global.m){
params_r.r = params_r.r + global.a[global.next[params_t.t]][0];
combine(params_t);
} else if (global.a[params_t.t][0] + global.a[global.prev[params_t.t]][0] === global.m){
t = global.prev[params_t.t];
combine(params_t);
}
}
}
function combine(params_t){
let x = global.next[params_t.t],
i = 0,
u = [];
for (let j=0; j<global.m; j++)
if (global.a[params_t.t][global.m + j - 1] < 0){
u[i] = global.a[params_t.t][global.m + j - 1];
i = i + 1;
}
for (let j=0; j<global.m; j++)
if (global.a[x][global.m + j - 1] < 0){
u[i] = global.a[x][global.m + j - 1];
i = i + 1;
}
build(u,global.a[params_t.t]);
global.next[params_t.t] = global.next[global.next[params_t.t]];
global.prev[global.next[params_t.t]] = params_t.t;
}
init(global);
algorithmL(global.n, global.b);(1) Л. Ван и Х. Ван. Сравнительное исследование алгоритмов для обобщенной проблемы Иосифа. Прикладная математика и информатика, 7, № 4, 1451-1457 (2013).
(2) Ссылки Уилсона (1979):
Кнут, Д.Е., Искусство компьютерного программирования, Эддисон-Уэсли, Рединг Масс., Том I Фундаментальные алгоритмы, 1968, Ex. 22, р158; Том III, Сортировка и поиск, напр. 2, с. 18-19; Том I, 2-е изд., С.181.
Аренс В., Mathematische Unterhaltungen und Spiele, Teubner: Лейпциг, 1901, глава 15, 286-301.
Капланский И., Герштейн И.Н., Математические вопросы, Челси, Нью-Йорк, 1978, с. 121-128.