Точность / отзыв для мультиклассовой-многослойной классификации

Question

Мне интересно, как рассчитать точность и вспомнить меры для мультиклассовой классификации с несколькими метками, то есть классификации, где существует более двух меток, и где каждый экземпляр может иметь несколько меток?

Answer 1

Для классификации по нескольким меткам у вас есть два пути. Сначала рассмотрите следующее.

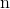• это количество примеров.
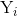• является наземным назначением правдивой метки 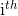пример..
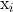• это 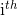пример.
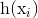• это предсказанные метки для 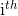пример.

Пример на основе

Метрики вычисляются в соответствии с назначением данных. Для каждой прогнозируемой метки вычисляется только ее оценка, а затем эти оценки агрегируются по всем точкам данных.

• Точность = 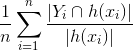Отношение того, сколько из предсказанного является правильным. Числитель находит, сколько меток в предсказанном векторе имеет общее с основной истинностью, а соотношение вычисляет, сколько из предсказанных истинных меток на самом деле находится в основной истине.
• Напомним = 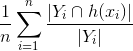Отношение того, сколько фактических ярлыков было предсказано. Числитель находит, сколько меток в прогнозируемом векторе имеет общее с основной истинностью (как указано выше), затем находит отношение к количеству фактических меток, получая, таким образом, какую долю фактических меток была предсказана.

Есть и другие метрики.

На основе метки

Здесь все сделано по меткам. Для каждой метки вычисляются метрики (например, точность, отзыв) и затем эти метрики для меток агрегируются. Следовательно, в этом случае вы в конечном итоге вычисляете точность / отзыв для каждой метки по всему набору данных, как вы делаете для двоичной классификации (так как каждая метка имеет двоичное назначение), а затем агрегируете ее.

Самый простой способ - представить общую форму.

Это просто расширение стандартного многоклассового эквивалента.

• Макро усредненный

• Микро усредненный

Здесь 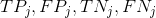являются истинно положительными, ложно положительными, истинно отрицательными и ложно отрицательными значениями соответственно только для 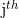этикетка

Здесь $B$ обозначает любую метрику на основе матрицы смешения. В вашем случае вы бы использовали стандартную точность и вызывали формулы. Для макро-среднего значения вы передаете счетчик для каждой метки, а затем сумму, для микро-среднего значения вы сначала усредняете значения, затем применяете свою метрическую функцию.

Возможно, вам будет интересно взглянуть на код метрик для нескольких меток, который входит в пакет mldr в R. Также вам может быть интересно заглянуть в библиотеку Java с несколькими метками MULAN.

Это хорошая статья, посвященная различным метрикам: обзор алгоритмов обучения по нескольким меткам

Answer 2

Ответ в том, что вы должны вычислить точность и вспомнить для каждого класса, а затем усреднить их вместе. Например, если вы классы A, B и C, то ваша точность:

(precision(A) + precision(B) + precision(C)) / 3

То же самое для отзыва.

Я не эксперт, но это то, что я определил, основываясь на следующих источниках:

https://list.scms.waikato.ac.nz/pipermail/wekalist/2011-March/051575.html http://stats.stackexchange.com/questions/21551/how-to-compute-precision-recall-for -multiclass-MultiLabel классификация

Answer 3

• Предположим, что у нас есть проблема мультиклассификации 3-го класса с метками A, B и C.
• Первое, что нужно сделать, это создать матрицу путаницы. Обратите внимание, что значения в диагонали всегда являются истинными положительными значениями (TP).

• Теперь, чтобы вычислить отзыв для метки A, вы можете прочитать значения из матрицы путаницы и вычислить:

  = TP_A/(TP_A+FN_A)
  = TP_A/(Total gold labels for A)
  

• Теперь давайте вычислим точность для метки A, вы можете считать значения из матрицы путаницы и вычислить:

  = TP_A/(TP_A+FP_A)
  = TP_A/(Total predicted as A)
  

• Вам просто нужно сделать то же самое для остальных меток B и C. Это относится к любой проблеме классификации нескольких классов.

Вот полная статья, в которой рассказывается о том, как вычислить точность и вспомнить любую проблему классификации с несколькими классами, включая примеры.

Answer 4

В питоне используя sklearn а также numpy:

from sklearn.metrics import confusion_matrix
import numpy as np

labels = ...
predictions = ...

cm = confusion_matrix(labels, predictions)
recall = np.diag(cm) / np.sum(cm, axis = 1)
precision = np.diag(cm) / np.sum(cm, axis = 0)

Answer 5

Простое усреднение подойдет, если классы сбалансированы.

В противном случае отзыв для каждого реального класса должен быть взвешен по распространенности класса, а точность для каждой предсказанной метки должна быть взвешена смещением (вероятностью) для каждой метки. В любом случае вы получите Рэнд Точность.

Более прямым способом является создание нормализованной таблицы сопряженности (деление на N, чтобы таблица складывалась до 1 для каждой комбинации метки и класса) и добавление диагонали для получения точности ранда.

Но если классы не сбалансированы, смещение остается, и метод с поправкой на случайность, такой как каппа, является более подходящим, или, что еще лучше, анализ ROC или метод правильной оценки вероятности, такой как информированность (высота над линией вероятности в ROC).