Разница между двоичным деревом и двоичным деревом поиска
Может кто-нибудь объяснить пример разницы между двоичным деревом идвоичным деревом поиска?
14 ответов
Двоичное дерево: дерево, в котором каждый узел имеет до двух листьев
1
/ \
2 3
Двоичное дерево поиска: используется для поиска. Двоичное дерево, в котором левый дочерний элемент содержит только узлы со значениями, меньшими, чем родительский узел, а правый дочерний элемент содержит только узлы, значения которых больше или равны родительскому.
2
/ \
1 3
Бинарное дерево - это специализированная форма дерева с двумя дочерними элементами (слева и справа от ребенка). Это просто представление данных в древовидной структуре
Двоичное дерево поиска (BST) - это особый тип двоичного дерева, которое соответствует следующему условию:
- левый дочерний узел меньше своего родительского узла
- правый дочерний узел больше, чем его родительский узел
Двоичное дерево состоит из узлов, где каждый узел содержит "левый" указатель, "правый" указатель и элемент данных. "Корневой" указатель указывает на самый верхний узел в дереве. Левый и правый указатели рекурсивно указывают на меньшие "поддеревья" с обеих сторон. Пустой указатель представляет двоичное дерево без элементов - пустое дерево. Формальное рекурсивное определение таково: двоичное дерево либо пустое (представлено нулевым указателем), либо состоит из одного узла, где левый и правый указатели (впереди рекурсивное определение) указывают на двоичное дерево.
Бинарное дерево поиска (BST) или "упорядоченное бинарное дерево" - это тип бинарного дерева, в котором узлы расположены по порядку: для каждого узла все элементы в его левом поддереве меньше узла (<), и все элементы в его правом поддереве больше, чем узел (>).
5
/ \
3 6
/ \ \
1 4 9
Дерево, показанное выше, является бинарным деревом поиска - "корневым" узлом является 5, а его левые узлы поддеревьев (1, 3, 4) имеют значение < 5, а его правые узлы поддеревьев (6, 9) -> 5. Рекурсивно, каждое из поддеревьев должно также подчиняться ограничению бинарного дерева поиска: в поддереве (1, 3, 4) 3 является корнем, 1 < 3 и 4 > 3.
Не упустите точную формулировку в задачах - "двоичное дерево поиска" отличается от "двоичного дерева".
Как все выше объяснили о разнице между двоичным деревом и двоичным деревом поиска, я просто добавляю, как проверить, является ли данное двоичное дерево бинарным деревом поиска.
boolean b = new Sample().isBinarySearchTree(n1, Integer.MIN_VALUE, Integer.MAX_VALUE);
.......
.......
.......
public boolean isBinarySearchTree(TreeNode node, int min, int max)
{
if(node == null)
{
return true;
}
boolean left = isBinarySearchTree(node.getLeft(), min, node.getValue());
boolean right = isBinarySearchTree(node.getRight(), node.getValue(), max);
return left && right && (node.getValue()<max) && (node.getValue()>=min);
}
Надеюсь, это поможет вам. Извините, если я отклоняюсь от темы, поскольку я чувствовал, что стоит упомянуть об этом здесь.
Двоичное дерево обозначает структуру данных, которая состоит из узлов, которые могут иметь только две дочерние ссылки.
Бинарное дерево поиска (BST), с другой стороны, представляет собой особую форму структуры данных Бинарного дерева, где каждый узел имеет сопоставимое значение, а дочерние элементы меньшего значения прикреплены к левому, а дочерние элементы большего значения - справа.
Таким образом, все BST являются двоичным деревом, однако только некоторые двоичные деревья могут быть также BST. Сообщите, что BST является подмножеством двоичного дерева.
Итак, Binary Tree - это более общая структура данных, чем Binary Search Tree. А также вы должны уведомить, что Двоичное дерево поиска является отсортированным деревом, тогда как для общего Двоичного дерева такого набора правил не существует.
Бинарное дерево
Binary Tree который не является BST;
5
/ \
/ \
9 2
/ \ / \
15 17 19 21
Двоичное дерево поиска (отсортированное дерево)
Двоичное дерево поиска, которое также является двоичным деревом;
50
/ \
/ \
25 75
/ \ / \
20 30 70 80
Свойство бинарного дерева поиска
Также сообщите, что для любого родительского узла в BST;
Все левые узлы имеют меньшее значение, чем значение родительского узла. В верхнем примере узлы со значениями { 20, 25, 30 }, которые все расположены слева (левые потомки) 50, меньше 50.
Все правые узлы имеют большее значение, чем значение родительского узла. В верхнем примере узлы со значениями { 70, 75, 80 }, которые все расположены справа (правые потомки) 50, больше 50.
Для узла Binary Tree такого правила не существует. Единственное правило для Binary Tree Node - иметь двоих детей, поэтому оно самоопределяется, поэтому и называется двоичным.
Бинарное дерево поиска - это особый вид бинарного дерева, которое обладает следующим свойством: для любого узла n значение каждого узла-потомка в левом поддереве n меньше значения n, а значение каждого узла-потомка в правом поддереве равно больше, чем значение n.
Бинарное дерево
Двоичное дерево может быть любым, у которого есть 2 дочерних и 1 родительский. Это может быть реализовано в виде связанного списка или массива, или с вашим пользовательским API. Как только вы начинаете добавлять более конкретные правила, оно становится более специализированным деревом. Наиболее распространенная известная реализация состоит в том, что добавьте меньшие узлы слева и более крупные справа.
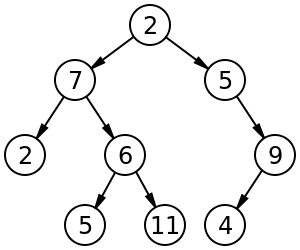
Например, помеченное двоичное дерево размером 9 и высотой 3 с корневым узлом, значение которого равно 2. Дерево не сбалансировано и не отсортировано. https://en.wikipedia.org/wiki/Binary_tree
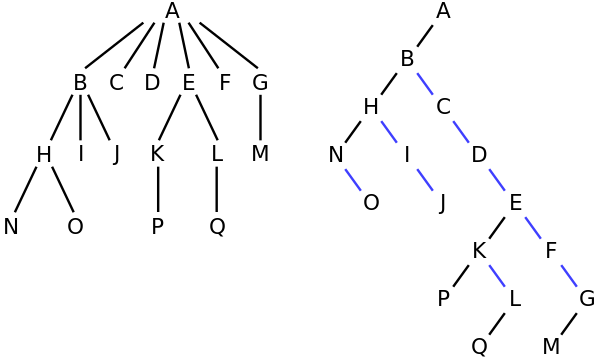
Например, в дереве слева у A есть 6 детей {B,C,D,E,F,G}. Это может быть преобразовано в двоичное дерево справа.
Бинарный поиск
Бинарный поиск - это метод / алгоритм, который используется для поиска определенного элемента в цепочке узлов. Двоичный поиск работает на отсортированных массивах.
Двоичный поиск сравнивает целевое значение со средним элементом массива; если они неравны, то половина, в которой цель не может находиться, удаляется, и поиск продолжается на оставшейся половине, пока она не будет успешной или оставшаяся половина не станет пустой. https://en.wikipedia.org/wiki/Binary_search_algorithm
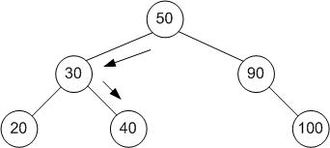
Дерево, представляющее бинарный поиск. Здесь ищется массив [20, 30, 40, 50, 90, 100], а целевое значение - 40.
Двоичное дерево поиска
Это одна из реализаций двоичного дерева. Это специализировано для поиска.
Двоичное дерево поиска и структуры данных B-дерева основаны на двоичном поиске.
Двоичные поисковые деревья (BST), иногда называемые упорядоченными или отсортированными двоичными деревьями, представляют собой особый тип контейнера: структуры данных, которые хранят "элементы" (такие как числа, имена и т. Д.) В памяти. https://en.wikipedia.org/wiki/Binary_search_tree
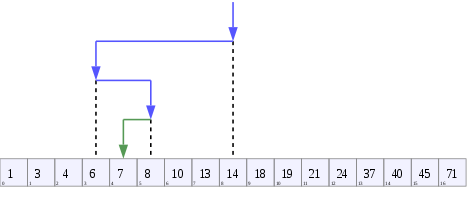
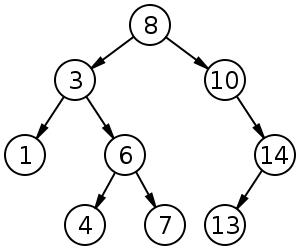
Двоичное дерево поиска размером 9 и глубиной 3, с 8 в корне. Листья не нарисованы.
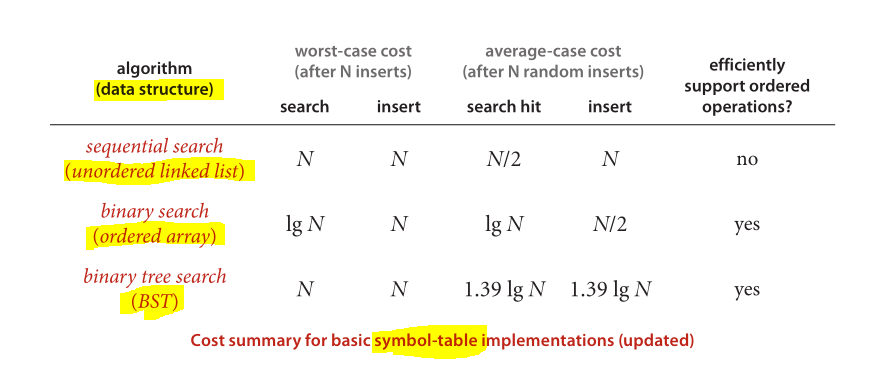
И, наконец, отличная схема для сравнения производительности известных структур данных и применяемых алгоритмов:
Изображение взято из алгоритмов (4-е издание)
- Бинарное дерево поиска: при обходе по порядку в двоичном дереве вы получаете отсортированные значения вставленных элементов.
- Двоичное дерево: в любом виде обхода не найдено отсортированного порядка
Бинарное дерево - это дерево, чьи дети никогда не превышают двух. Бинарное дерево поиска следует инварианту того, что левый потомок должен иметь меньшее значение, чем ключ корневого узла, в то время как правый потомок должен иметь большее значение, чем ключ корневого узла.
Чтобы проверить, является ли данное Двоичное дерево бинарным деревом поиска, вот альтернативный подход.
Дерево обхода Inorder Fashion (т. Е. Left Child -> Parent -> Right Child), Хранить данные пройденного узла во временной переменной, скажем, temp, непосредственно перед сохранением в temp, Проверьте, не являются ли данные текущего узла выше, чем предыдущие или нет, Тогда просто разбейте его, дерево не является бинарным деревом поиска, пока не пройдете до конца.
Ниже приведен пример с Java:
public static boolean isBinarySearchTree(Tree root)
{
if(root==null)
return false;
isBinarySearchTree(root.left);
if(tree.data<temp)
return false;
else
temp=tree.data;
isBinarySearchTree(root.right);
return true;
}
Поддерживать временную переменную снаружи
Дерево может быть названо двоичным деревом тогда и только тогда, когда максимальное число дочерних элементов любого из узлов равно двум.
Дерево можно назвать бинарным деревом поиска тогда и только тогда, когда максимальное число дочерних элементов любого из узлов равно двум, а левый дочерний элемент всегда меньше правого дочернего элемента.
В бинарном дереве поиска все узлы расположены в определенном порядке - узлы слева от корневого узла имеют меньшее значение, чем его корень, а все узлы справа от узла имеют значения, превышающие значение корень.
Бинарное дерево — это дерево, в котором каждая вершина может иметь не более двух потомков.
Двоичное дерево поиска является его дальнейшей модификацией, придающей определенную связь родителю и двум дочерним элементам. Так как есть только два ребенка, т. е. левый и правый ребенок; отношение определяется следующим образом:
Левый дочерний элемент <= родитель <= правый дочерний элемент
Это на самом деле так просто.
В бинарном дереве у каждого узла есть 2 дочерних узла: левый узел и правый узел. Двоичное дерево поиска — это особый вид дерева, в котором узлы отсортированы, левый узел меньше родительского узла, а левый узел больше родительского узла. Бинарное дерево допускает повторяющиеся значения, двоичное дерево поиска не допускает дублирования значений, а также выполнение любых операций в двоичном дереве поиска выполняется быстрее, чем в двоичном дереве, поскольку BST сортируется