ElGamal проверка подписи

Question

Я пытаюсь реализовать подпись ElGamal, но у меня проблемы с проверкой. Согласно википедии, подпись (r,s) сообщения m является правильной, если: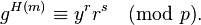

Существует известный алгоритм расчета ModPow, который используется на шаге подписи: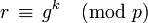

Но я не могу найти способ рассчитать первую формулу. Кажется, что это будет слишком большое число, если я попытаюсь рассчитать мощность напрямую. Я кодирую на C# и использую BigInteger, который даже не позволяет рассчитать мощность по показателю BigInteger - принимаются только общие целые числа, что, я полагаю, разумно.
Есть ли какое-то упрощение? Как это должно быть рассчитано? Спасибо

Answer 1

Вы рассчитываете его, используя точно такой же алгоритм, который вы используете для вычисления g^k (mod p), квадрат и умножить. Вам не нужно реализовывать этот алгоритм самостоятельно, ModPow метод является частью BigInteger тип.

bool success = BigInteger.ModPow(g, h, p) ==
               (BigInteger.ModPow(y, r, p) + BigInteger.ModPow(r, s, p)) % p;

Обратите внимание, что (mod p) справа математическая формула не является оператором, она говорит вам, что все уравнение следует рассматривать как конгруэнтность по модулю р.

Answer 2

Да, вы можете использовать библиотеку gmp, связав опцию -lgmp.
Хотя в Python есть большое число, скорость вычислений слишком мала для использования.
Это пример проверки параметров вывода OpenSSL в DSA。 Используйте эту функцию:

Функция: void mpz_powm (mpz_t rop, const mpz_t base, const mpz_t exp, const mpz_t mod)

#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <assert.h>
#include "gmp.h"
int main()
{
    mpz_t P;    // a big prime
    mpz_t Q;    // order
    mpz_t G;    // generator 
    mpz_t pub;  // public key
    mpz_t priv; // private key
    mpz_t tmp; //  tmp variable

    //  Initialize a NULL-terminated list of mpz_t variables, and set their values to 0.
    mpz_inits (P ,Q, G, pub, priv,  tmp, NULL);

    mpz_set_str (P, "0x00e79d25ca547dc8931850eaaa6784e365eecf69374243d902c12df7d4896a9e5b8717c4c7b24e30d1b468061838f5bc76df050ef6b7c58105ee2cf23ecb67e7d89830a0976f606e194d0b85e6566cca6275b7b184416337fc7ac37bebe9c9f76e982b9a82ee0a904900a0a7f76f4760e76120ecd2732a1dfe9a1dfa568757690670460688205a7e0d744feacdc27416a27afe5233dd58945801af83c7fd7199dcbed00819750c81cd3f2b5d68c29cd43e035eed70bfd85f55259df953f4f69d719ebe5c06b3443d249b110e602d81366ea88407ed81d3cf6f6fcea1bb7f9af563d2ca436d5c2d794f06407d1f111cb25a86f7568368e085ebe31f7eb8b9bedb89", 0); //  the prime P 
    mpz_set_str (Q, "0x00c39250922561c4b56a9c1bfb0d523bbfe8395182c5464b38a1d9959aa121871b", 0); // the order 
    mpz_set_str (G, "0x6cde6920c61fa80e51212de15be6b2aca93174e3fd5d479d08affb57222370c9047b099ea9e9d53b694915967709580b77a5cfd70629e1308c9db7a9e8c2f41f3c7c792c9ffe9dd6695bbc549d2a008005c18e75096c9d455de4d75011dfaa4d18df4ee955de3da692b2a49084285794d9e53df199b0dd5514bee1e387e897d971b6e56f9dcb49bf8a5a4470bf0216816b4ce1ab498957cb5dcc4ef64146a1a424b2d829fe29215e998590213053735618df90485353cee4702194c4de66bd77c3d9cf0fa45ef4b64b5c41186735b46805d2eaf91542507a28805db5838ac3d17ed3227764f5b80d19d8f752f58f01eec5ba12a4c8375a5a47b11f0dc36c2679", 0);  // generator
    mpz_set_str (priv, "0x404dcd0061be1e3d4e5dac6322600d442c1f55fd15b5ecc3d6ad52b527cf44b8", 0); // private key 
    mpz_set_str (pub, "0x71fd06b1b4c4ea7b392b6f33486063db6fe318559046bf750e4b236d59b883ca9174b3e8c9fc788aa2b926d2eaddd36fa7610e6d91822818a69526057d65c4fe1f7e7620ac54164c21ea2c27783eeb58880a3758b7b8f570383c964f37756f5b331d2afda9bc104e99d1a7fb2d29abf9017fac13cf87b4a6d18838c16aa52e130a3ca1b8b88ce830f982200c5dba7369934af4aee15a83963874b0c04d1fd57cf7525b46e4add4f57c892fefa698be330c22282145ada2589a1a2d2816c470164341a8482de9ad72ed1d636a7836b91218932c565c2b5a5ab03ca5704ca5da13904e0bbd6288d99a9827b751de19bb7c165ce3d910f94f43d6166def03aa895b", 0); // public key 

    // verify (G^Q)%P==1
    //Negative exp is supported if an inverse base^-1 mod mod exists (see mpz_invert in Number Theoretic Functions). If an inverse doesn’t exist then a divide by zero is raised.
    mpz_powm(tmp, G, Q, P);
    printf("the modulus :");
    mpz_out_str(stdout, 10, tmp);
    printf("\n");

    // verify the private == public key 
    mpz_powm(tmp, G, priv, P);
    int result = mpz_cmp(tmp, pub);
    printf("the result:%d\n", result);
}

Его можно составить как:

Установите пакет в системе debian

 sudo aptitude install libgmp-dev      

компилировать

   g++ -Wall -g -lgmp   dsa_alg.cpp -o dsa_alg  

запустить./dsa_alg

  the modulus :1     
  the result:0   

Answer 3

Я реализовал алгоритм в Matlab и он работает нормально. Я использовал переменную точность целого числа (vpi) для больших чисел.

zvyr = vpi(mod(((y^r)*(r^s)),p))

Я верю, что нечто подобное будет доступно для C#.