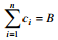Алгоритмы. Динамическое программирование. Подмножество двух массивов

Question

Моя домашняя работа включает в себя вопрос динамического программирования:

Даны два массива натуральных целых чисел (a1,a2,...,an и b1,b2,...,bn), все они меньше n^2, а также задано число B, которое меньше n^3.

Вам нужно сдерживать, если есть массив (c1,c2,...,cn) такой:

И для каждого 1 <= i <= n, ci = ai или ci = bi.

* Этот алгоритм должен быть написан с динамическим программированием.

* Кроме того, что нам нужно изменить, чтобы фактически получить массив c, который дает нам Sum(c) = B

Другой способ взглянуть на вопрос - сказать, что c равно подмножеству a, а его подмножество дополнения - из b.

Это рекурсивный псевдокод, который я написал для решения этого вопроса:

W(a,b,i, N)
    if i==-1
        if N==0     return true;
        else        return false;
    return W(a,b,i-1,N-a[i]) || W(a,b,i-1,N-b[i]);

T(n) = 2^n

И здесь, чтобы вернуть лучший путь, просто сохраните его в дереве и перейдите от (хорошего) конца к началу

Как я могу написать это с динамическим программированием? Поможет ли это даже во время выполнения? потому что рекурсивное решение имеет независимые результаты.

* Я искал в Google эту проблему и не нашел ничего, кроме "проблемы с подмножеством", которая отличается.

Answer 1

Благодаря @PhamTrung у меня есть решение:

Пусть будет матрица [B,n] (максимальный размер [n^3,n])

Пример: (n=3, B=8)

    0   1       2       3       4       ... 8
0   T   F       F       F       F       ... F
1   F   (1,1)   (1,2)   (1,3)   (1,4)   ... (1,8)
2   F   F       (2,2)   (2,3)   (2,4)   ... (2,8)
3   F   F       F       (3,3)   (3,4)   ... (3,8)

Псевдокод:

//Generate the matrix
A = new Array(n+1,B+1)
for(i: 0 to n) //run over lines
    for(j: 0 to B) //run over B columns
        if i==0 //if we are in the first row
            A[i,j] = j==0; //if this is [0,0], it is true. else, false
        else if i>j //if we have more numbers than the sum
            A[i,j] = false; //it cannot happen
        else
            //general case:
            //if we remove a[i] or b[i], will we get to a true statement?
            A[i,j] = (j-a[i] >= 0 && A[i-1, j-a[i]]) || (j-b[i] >= 0 && A[i-1, j-b[i]]);

is_set(n,B,A)
    if(A[n,B])
        return true;
    return false;

Формулы:

[0,j],j!=0 = F
[0,0]   = T
i > j   = F
i <= j  = (i-1, j - a[i]) || (i-1, j - b[i])

Получение маршрута:

Чтобы получить маршрут построения C, мы также сохраним в каждой истинной точке 0(=a) или 1(=b) и просто перейдем снизу вверх.