2-я интерполяция, игнорирующая значения nan

Question

Как вы говорите interp2d игнорировать значения nan?

У меня есть поверхность x и y с некоторым произвольным значением z.

x =   np.array([[9.19632, 9.62141, 10.0829, np.isnan, np.isnan],
        [9.21164, 9.64347, 10.1392, 10.5698,  np.isnan],
        [9.22175, 9.65439, 10.1423, 10.6301, 11.0323],
        [9.21632, 9.67060, 10.1474, 10.6230, 11.0818]])

y =  np.array([[11.5466,11.6485,11.7619, np.isnan, np.isnan],
        [12.4771, 12.5460, 12.5453, 12.7142, np.isnan],
        [13.5578, 13.5581, 13.5505, 13.5309, 13.6081],
        [14.5653, 14.5504, 14.5036, 14.5145, 14.5060]])

z = np.array([[0.466113, 0.0484404, -0.385355, np.isnan, np.isnan],
        [0.366125, -0.160165, -0.548668, -0.888301,np.isnan],
        [-0.0970777, -0.346734, -0.826576, -1.08412, -1.33129],
        [-0.259981, -0.586938, -1.03477, -1.32384, -1.61500]])

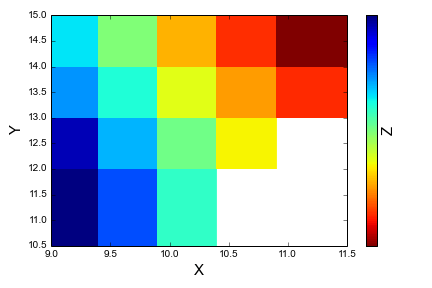
Я был в состоянии создать вышеупомянутую цветную сетку, используя маскированный массив, но у меня не получается, когда я пытаюсь создать более точную сетку, используя 2-мерную интерполяцию. Ниже приведено то, что у меня есть, обратите внимание, что я установил значения nan на ноль, чтобы получить это, так что очевидно, что это испортило "правильную" интерполяцию. Вместо этого я хотел бы игнорировать их и оставить пустым пространство параметров.

f = interp.interp2d(x,y,z, kind='linear')
xnew = np.arange(9,11.5, 0.01)
ynew = np.arange(9,15, 0.01)
znew = f(xnew, ynew)


levels = np.linspace(zmin, zmax, 15)
plt.ylabel('Y', size=15)
plt.xlabel('X', size=15)
cmap = plt.cm.jet_r
cmap.set_bad('white',0.1) # set nan to white
cs = plt.contourf(xnew, ynew, znew, levels=levels, cmap=cmap)
cbar = plt.colorbar(cs)
cbar.set_label('Z', rotation=90, fontsize=15) # gas fraction
plt.show()

Я хочу просто создать гладкую цветную диаграмму, где области, ограниченные x и y, окрашены в соответствии с z.

Answer 1

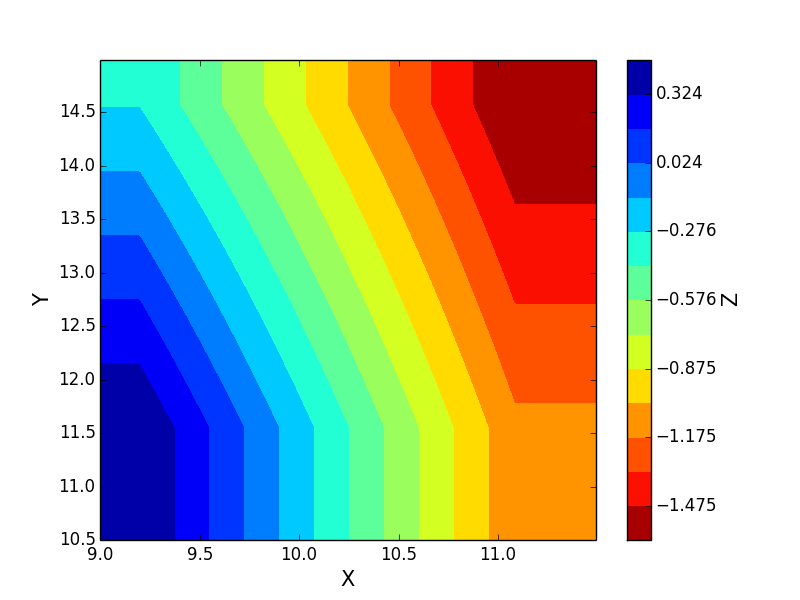
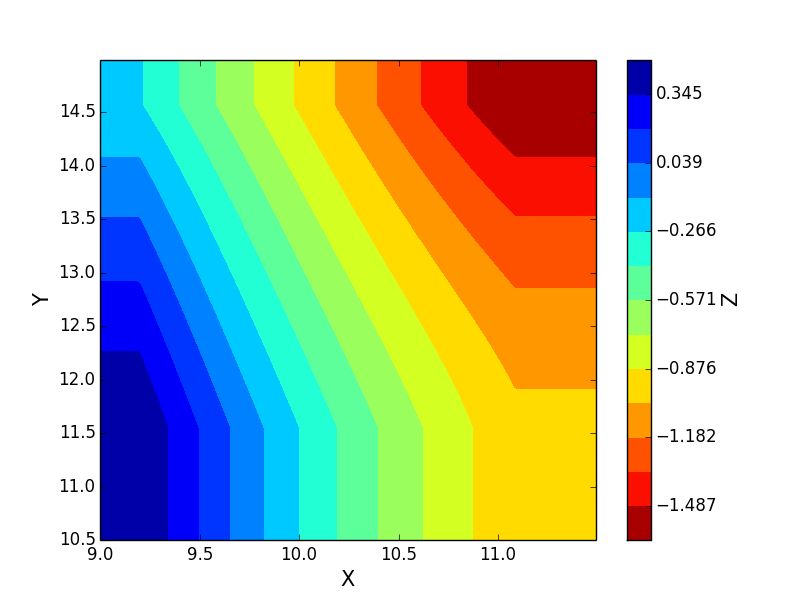
Я не знаю, почему у interp2d проблемы с нерегулярно расположенными данными, я бы порекомендовал использовать griddata, вы можете выровнять свои входные данные в вектор с ravel а затем исключить NaN и использовать его в качестве ввода griddata, вы получите что-то вроде этого

Код не сильно отличается от того, что у вас есть

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import griddata

x =   np.array([[9.19632, 9.62141, 10.0829,np.isnan,np.isnan],
    [9.21164, 9.64347, 10.1392, 10.5698,np.isnan],
    [9.22175, 9.65439, 10.1423, 10.6301, 11.0323],
    [9.21632, 9.67060, 10.1474, 10.6230, 11.0818]])

y =  np.array([[11.5466,11.6485,11.7619,np.isnan,np.isnan],
    [12.4771, 12.5460, 12.5453, 12.7142,np.isnan],
    [13.5578, 13.5581, 13.5505, 13.5309, 13.6081],
    [14.5653, 14.5504, 14.5036, 14.5145, 14.5060]])

z = np.array([[0.466113, 0.0484404, -0.385355,np.isnan,np.isnan],
    [0.366125, -0.160165, -0.548668, -0.888301,np.isnan],
    [-0.0970777, -0.346734, -0.826576, -1.08412, -1.33129],
    [-0.259981, -0.586938, -1.03477, -1.32384, -1.61500]])

x=x.ravel()              #Flat input into 1d vector
x=list(x[x!=np.isnan])   #eliminate any NaN
y=y.ravel()
y=list(y[y!=np.isnan])
z=z.ravel()
z=list(z[z!=np.isnan])


xnew = np.arange(9,11.5, 0.01)
ynew = np.arange(9,15, 0.01)
znew = griddata((x, y), z, (xnew[None,:], ynew[:,None]), method='linear')



levels = np.linspace(min(z), max(z), 15)
plt.ylabel('Y', size=15)
plt.xlabel('X', size=15)
cmap = plt.cm.jet_r
cs = plt.contourf(xnew, ynew, znew, levels=levels, cmap=cmap)
cbar = plt.colorbar(cs)
cbar.set_label('Z', rotation=90, fontsize=15) # gas fraction
plt.show()

---

Если вы должны экстраполировать данные (проверьте мой комментарий ниже), вы можете использовать SmoothBivariateSpline и поиграть с порядком сплайна, я не рекомендую, я покажу вам, почему.

Код ближе к тому, что вы имели изначально.

from scipy.interpolate import SmoothBivariateSpline

x=x.ravel()
x=(x[x!=np.isnan])
y=y.ravel()
y=(y[y!=np.isnan])
z=z.ravel()
z=(z[z!=np.isnan])

xnew = np.arange(9,11.5, 0.01)
ynew = np.arange(10.5,15, 0.01)

f = SmoothBivariateSpline(x,y,z,kx=1,ky=1)

znew=np.transpose(f(xnew, ynew))

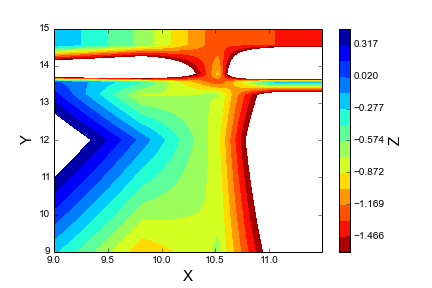
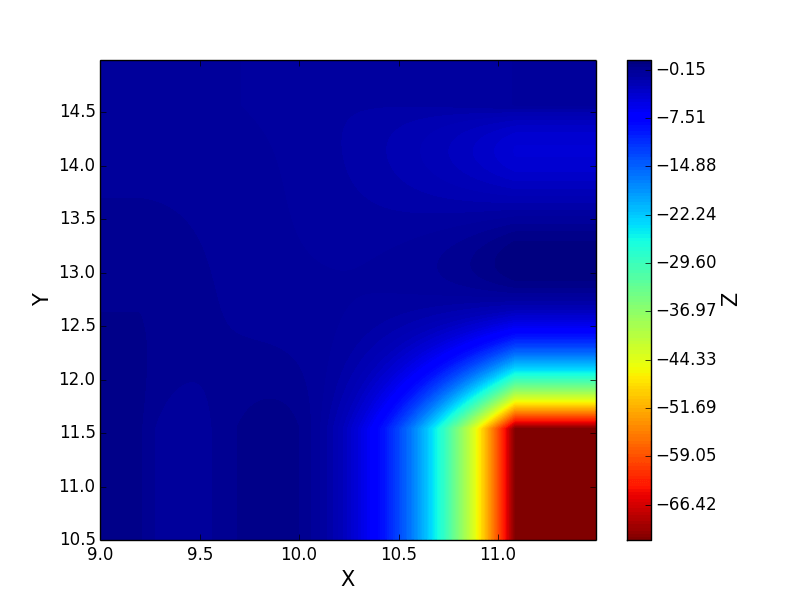
С kx=1 и ky=1 f = SmoothBivariateSpline(x,y,z,kx=1,ky=1) ты получаешь

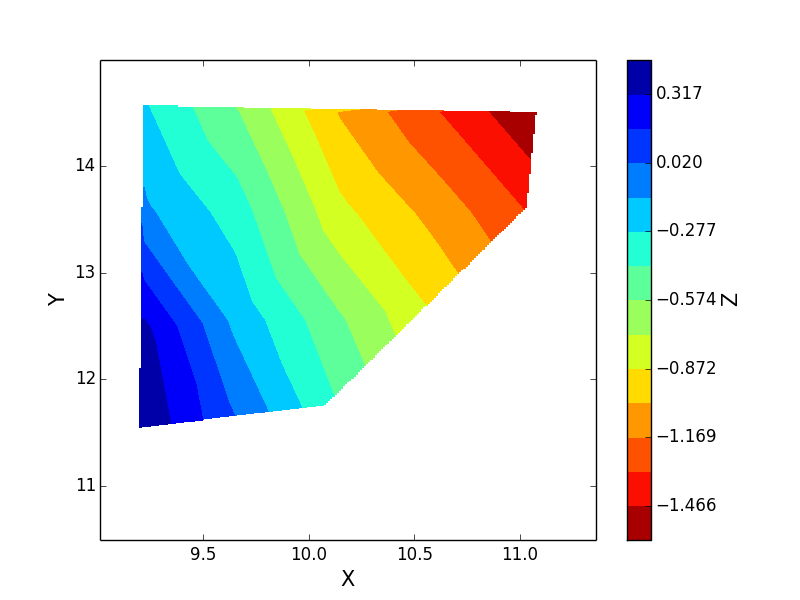
С kx=2 и ky=2 вы получите:

И с kx=3 и ky=3 вы получите:

Я изменил уровни на 3 картинках, чтобы их было легче увидеть. Но проверьте масштаб, значения могут очень быстро сойти с ума за пределами вашей области выборки, поэтому, если вы ДОЛЖНЫ экстраполировать, делайте это с усердием