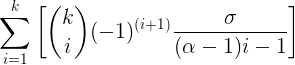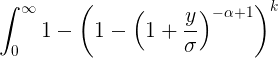Обработка суммирования больших биномов в Python
Мне нужно вычислить эту формулу:
Это приближение этого интеграла
но это не имеет значения, на самом деле я просто хочу вычислить значение рисунка 1 с помощью PYTHON, это то, что касается темы.
K, альфа и сигма являются фиксированными значениями в пределах одного вычисления, обычно:
- 0 <= k <= 99;
- альфа = 3;
- сигма = 2.
Ниже показано, как я пытаюсь вычислить такое суммирование в python:
import decimal
from scipy.special import binom
def residual_time_mean(alpha, sigma=2, k=1):
prev_prec = decimal.getcontext().prec
D = decimal.Decimal
decimal.getcontext().prec = 128
a = float(alpha)
s = float(sigma)
sum1 = 0.0
sum2 = 0.0
sumD1 = D(0.0)
sumD2 = D(0.0)
for i in range(1, k + 1):
sum1 += binom(k, i) * ((-1) ** (i + 1)) * (s / ((a - 1) * i - 1.0))
sum2 += binom(k, i) * ((-1) ** (i + 1)) * s / ((a - 1) * i - 1.0)
sumD1 += D(binom(k, i)) * (D(-1.0) ** (D(i) + D(1.0))) * (D(s) / ((D(a) - D(1.0)) * D(i) - D(1.0)))
sumD2 += D(binom(k, i)) * (D(-1.0) ** (D(i) + D(1.0))) * D(s) / ((D(a) - D(1.0)) * D(i) - D(1.0))
decimal.getcontext().prec = prev_prec
return sum1, sum2, float(sumD1), float(sumD2)
Бег
for k in [0, 1, 2, 4, 8, 20, 50, 99]:
print("k={} -> {}".format(k, residual_time_mean(3, 2, k)))
результат:
k=0 -> (0.0, 0.0, 0.0, 0.0)
k=1 -> (2.0, 2.0, 2.0, 2.0)
k=2 -> (3.3333333333333335, 3.3333333333333335, 3.3333333333333335, 3.3333333333333335)
k=4 -> (5.314285714285714, 5.314285714285714, 5.314285714285714, 5.314285714285714)
k=8 -> (8.184304584304588, 8.184304584304583, 8.184304584304584, 8.184304584304584)
k=20 -> (13.952692275798238, 13.952692275795965, 13.95269227579524, 13.95269227579524)
k=50 -> (23.134878809207617, 23.13390225415814, 23.134078892910786, 23.134078892910786)
k=99 -> (265412075330.96634, 179529505602.9507, 17667813427.20196, 17667813427.20196)
Вы можете видеть, что начиная с k=8 результаты разные.
Умножение перед делением приводит к результатам sum1 а также sum2 например, расходиться много для k=99.
sum1 += binom(k, i) * ((-1) ** (i + 1)) * (s / ((a - 1) * i - 1.0))
sum2 += binom(k, i) * ((-1) ** (i + 1)) * s / ((a - 1) * i - 1.0)
С десятичной дробью эта проблема не возникает, но результат не является правильным.
Вычисление суммирования на WolframAlpha
для к = 99
( Вот ссылка для расчета на WolframAlpha). Это дает 33.3159488(...), в то время как для моей функции python это 17667813427.20196. Я доверяю WolframAlpha, так как он делает что-то вроде символьных вычислений, на самом деле он также возвращает реальное значение в виде дроби.
для других к
Проблемы аппроксимации (например, значение, вычисленное Wolfram, отличается от значения, вычисленного в python на порядок 10^0 или более), начинаются с k~=60.
Кроме того, вычисляя интеграл (рисунок 2) с scipy.integrate приводит к аналогичным ошибкам аппроксимации.
Вопрос:
Есть ли у вас какие-либо предложения для обработки этого вычисления? Увеличение десятичной точности не кажется полезным.
2 ответа
Я не понимаю, почему вы привлекаете numpy функция здесь, и почему вы переходите к float объекты. Действительно, для этой формулы, если ваши входные данные всегда целые, то просто придерживайтесь int а также fractions.Fraction и ваши ответы всегда будут точными. Это достаточно легко реализовать свой собственный binom функция:
In [8]: def binom(n, k):
...: return (
...: factorial(n)
...: // (factorial(k)*factorial(n-k))
...: )
...:
Обратите внимание, я использовал целочисленное деление: //, И, наконец, ваше суммирование:
In [9]: from fractions import Fraction
...: def F(k, a, s):
...: result = Fraction(0, 1)
...: for i in range(1, k+1):
...: b = binom(k, i)*pow(-1, i+1)
...: x = Fraction(s, (a-1)*i - 1)
...: result += b*x
...: return result
...:
И результаты:
In [10]: F(99, 3, 2)
Out[10]: Fraction(47372953498165579239913571130715220654368322523193013011418, 1421930192463933435386372127473055337225260516259631545875)
Что кажется правильным на основе вольфрам-альфа...
Обратите внимание, если сказать, alpha может быть нецелым числом, вы можете использовать decimal.Decimal для операций с плавающей запятой произвольной точности:
In [17]: from decimal import Decimal
...: def F(k, a, s):
...: result = Decimal('0')
...: for i in range(1, k+1):
...: b = binom(k, i)*pow(-1, i+1)
...: x = Decimal(s) / Decimal((a-1)*i - 1)
...: result += b*x
...: return result
...:
In [18]: F(99, 3, 2)
Out[18]: Decimal('33.72169506311642881389682714')
Давайте повысим точность:
In [20]: import decimal
In [21]: decimal.getcontext().prec
Out[21]: 28
In [22]: decimal.getcontext().prec = 100
In [23]: F(99, 3, 2)
Out[23]: Decimal('33.31594880623309576443774363783112352607484321721989160481537847749994248174570647797323789728798446')
Я обнаружил проблему самостоятельно:
проведение scipy.special.binom(99,50) дает
5.044567227278209e+28
при расчете бинома (99,50) на WolframAlpha дает
5.0445672272782096667406248628e+28
Существует абсолютная разница с порядком величины 10^12.
Поэтому, конечно, результаты функции python ненадежны при больших значениях k. Поэтому мне нужно изменить способ вычисления бинома.