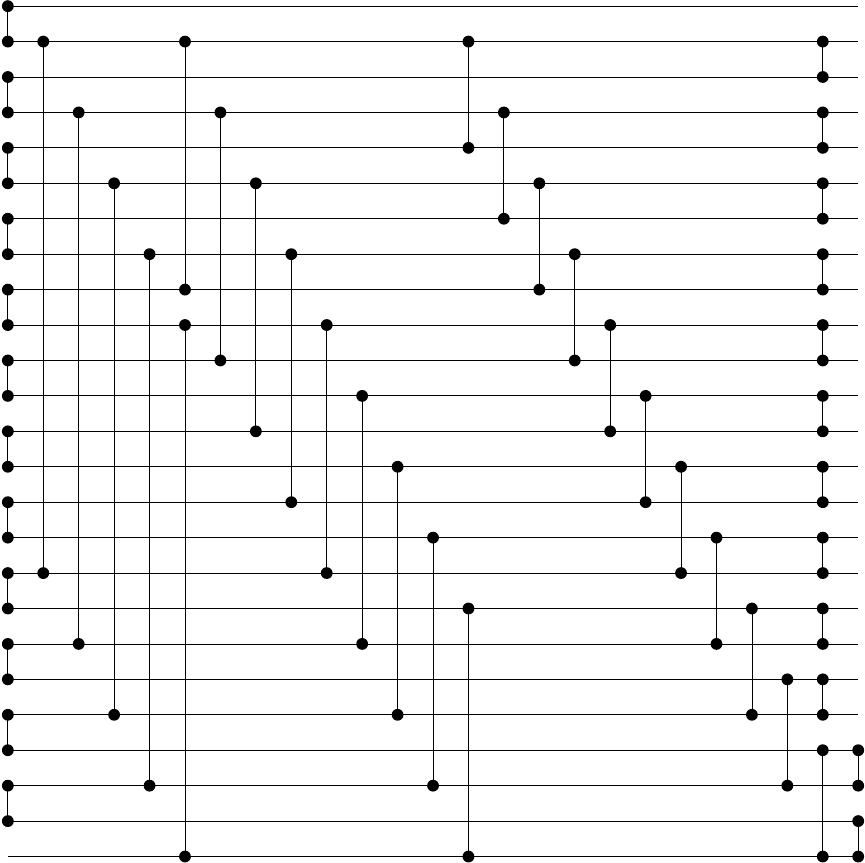
Оптимальные нечетно-четные сети слияния Батчера для размеров, отличных от 2^n

Question

В эти дни я пытался реализовать сортировку сетей до размера 32 с минимальным количеством единиц сравнения-обмена (оптимальных по размеру, а не по глубине). На данный момент я могу использовать следующие ресурсы для создания своих сетей:

• Сортировка сетей от 0 до 16: Perl's Algorithm::Networksort модуль с "лучшим" алгоритмом. К сожалению, он предоставляет только самые известные сети до размера 16.

• Сортировка сетей с 17 по 23: использование симметрии и эволюционного поиска для минимизации сортировочных сетей. Автор Valsalam и Miikkulainen.

В статье " Поиск лучших сетей сортировки " Баддара дается минимальное количество единиц обмена для сравнения, известных для сортировки сетей от 0 до 32 (не актуально, поскольку Valsalam и Miikkulainen предоставляют лучшие алгоритмы для размеров 17, 18, 19). 20, 21 и 22) и метод, используемый для их поиска: в основном, необходимо разделить массив на две, а затем отсортировать обе половины, используя наиболее известные сети сортировки для этих размеров, прежде чем объединять их с использованием нечетно-четной сети слияния (что соответствует шагу слияния нечетно-четного слияния Дозатора).

Страница Wikipedia дает следующую реализацию Python для нечетно-четного слияния Бэтчера:

def oddeven_merge(lo, hi, r):
    step = r * 2
    if step < hi - lo:
        yield from oddeven_merge(lo, hi, step)
        yield from oddeven_merge(lo + r, hi, step)
        yield from [(i, i + r) for i in range(lo + r, hi - r, step)]
    else:
        yield (lo, lo + r)

def oddeven_merge_sort_range(lo, hi):
    """ sort the part of x with indices between lo and hi.

    Note: endpoints (lo and hi) are included.
    """
    if (hi - lo) >= 1:
        # if there is more than one element, split the input
        # down the middle and first sort the first and second
        # half, followed by merging them.
        mid = lo + ((hi - lo) // 2)
        yield from oddeven_merge_sort_range(lo, mid)
        yield from oddeven_merge_sort_range(mid + 1, hi)
        yield from oddeven_merge(lo, hi, 1)

def oddeven_merge_sort(length):
    """ "length" is the length of the list to be sorted.
    Returns a list of pairs of indices starting with 0 """
    yield from oddeven_merge_sort_range(0, length - 1)

oddeven_merge Шаг уже изолирован, поэтому его было легко использовать отдельно для генерации пар индексов, необходимых для объединения двух отсортированных половинок исходного массива. Однако эта реализация работает только тогда, когда размер массива равен степени 2. Следовательно, он позволил мне найти только минимально известное количество единиц сравнения-обмена, необходимое для сети сортировки размером 32. Удаление пар индексов с помощью Наивысший индекс позволил мне найти эквивалентную сеть сортировки размером 31, но удаление большего количества пар не дало лучших результатов для размеров, меньших 31.

в Perl Algorithm::Networksort Модуль предоставляет альтернативную реализацию нечетно-четного слияния Бэтчера, которая работает с массивами любого размера, а не только степенями 2. Поэтому я решил взглянуть на него, чтобы посмотреть, смогу ли я извлечь шаг слияния из алгоритма. Вот эквивалент Python (он также соответствует алгоритму, описанному Кнутом в книге "Искусство компьютерного программирования", том 3):

def oddeven_merge_sort(length):
    t = math.ceil(math.log2(length))

    p = 2 ** (t - 1)

    while p > 0:
        q = 2 ** (t - 1)
        r = 0
        d = p

        while d > 0:
            for i in range(length - d):
                if i & p == r:
                    yield (i, i + d)

            d = q - p
            q //= 2
            r = p
        p //= 2

К сожалению, этот алгоритм кажется мне немного загадочным, и я не смог извлечь из него сливающуюся часть. Мне удалось получить объединяющуюся сеть, которая дала мне минимально известное количество единиц сравнения-обмена, необходимое для сортировочной сети размером 24, но использованный трюк не масштабировался до каких-либо других размеров (и, насколько я понимаю, это определенно не было нечетно-четное слияние).

Я попробовал еще пару вещей, чтобы адаптировать шаг слияния из нечетно-четного слияния Бэтчера для массивов, размер которых не является степенью двойки, но я не смог найти самые известные сети сортировки для размеров 25, 26, 27, 28, 29 и 30. Как я могу получить этот шаг слияния, чтобы найти недостающие части головоломки?

Answer 1

Алгоритм Perl упоминает в комментарии, что это алгоритм 5.2.2M в поиске и сортировке Кнута.

В свою очередь, Кнут упоминает, что он объединяет отсортированные последовательности вместе с тем, когда p = 1. Таким образом, для генерации ваших пар, которые объединяют последовательность для любого N, вы просто запускаете алгоритм с p = 1:

def oddeven_merge_step(length):
    t = math.ceil(math.log2(length))
    q = 2 ** (t - 1)
    r = 0
    d = 1

    while d > 0:
        for i in range(length - d):
            if i & 1 == r:
                yield (i, i + d)

        d = q - 1
        q //= 2
        r = 1

Обратите внимание, что шаг слияния нечетного и четного Бэтчера предполагает, что отсортированные последовательности чередуются (четные, нечетные, четные, ...), но создает последовательную сортированную последовательность.

Например, для N = 25 генерируется следующая сеть: