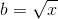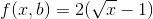Как я могу написать степенную функцию сам?
Мне всегда было интересно, как я могу сделать функцию, которая рассчитывает мощность (например, 23) самостоятельно. На большинстве языков они включены в стандартную библиотеку, в основном как pow(double x, double y), но как я могу написать это сам?
Я думал о for loops, но он думает, что мой мозг зациклился (когда я хотел сделать мощность с нецелым показателем, например, 54,5 или минус 2-21), и я сошел с ума;)
Итак, как я могу написать функцию, которая вычисляет мощность действительного числа? Спасибо
О, может быть важно отметить: я не могу использовать функции, которые используют полномочия (например, exp), что сделало бы это в конечном итоге бесполезным.
13 ответов
Отрицательные силы не проблема, они просто обратное (1/x) положительной силы.
Сила с плавающей запятой немного сложнее; как вы знаете, дробная сила эквивалентна корню (например, x^(1/2) == sqrt(x)) и вы также знаете, что умножение степеней с одной и той же базой эквивалентно добавлению их показателей.
Со всем вышеперечисленным вы можете:
- Разложить показатель степени на целую часть и рациональную часть.
- Рассчитайте целочисленную мощность с помощью цикла (вы можете оптимизировать его, разложив по коэффициентам и повторно используя частичные вычисления).
- Вычислите корень с помощью любого алгоритма, который вам нравится (любая итерационная аппроксимация, например, деление пополам или метод Ньютона, может сработать).
- Умножьте результат.
- Если показатель был отрицательным, примените обратное.
Пример:
2^(-3.5) = (2^3 * 2^(1/2)))^-1 = 1 / (2*2*2 * sqrt(2))
AB = Log-1(Log (A) * B)
Изменить: да, это определение действительно предоставляет что-то полезное. Например, на x86 это переводит почти напрямую FYL2X (Y * Log2(X)) и F2XM1 (2х-1):
fyl2x
fld st(0)
frndint
fsubr st(1),st
fxch st(1)
fchs
f2xmi
fld1
faddp st(1),st
fscale
fstp st(1)
Код заканчивается немного дольше, чем вы могли ожидать, в первую очередь потому, что F2XM1 работает только с числами в диапазоне -1.0..1.0. fld st(0)/frndint/fsubr st(1),st Часть вычитает из целочисленной части, поэтому у нас остается только дробь. Мы применяем F2XM1 к этому, добавьте 1 обратно, затем используйте FSCALE обрабатывать целую часть возведения в степень.
Как правило, реализация pow(double, double) Функция в математических библиотеках основана на идентичности:
pow(x,y) = pow(a, y * log_a(x))
Используя эту личность, вам нужно только знать, как поднять одно число a к произвольному показателю, и как взять основание логарифма a, Вы фактически превратили сложную многопараметрическую функцию в две функции одной переменной и умножения, которое довольно легко реализовать. Наиболее часто выбираемые значения a являются e или же 2 - e поскольку e^x а также log_e(1+x) иметь некоторые очень хорошие математические свойства, и 2 потому что он имеет некоторые хорошие свойства для реализации в арифметике с плавающей точкой.
Преимущество такого способа заключается в том, что (если вы хотите получить полную точность) вам необходимо вычислить log_a(x) срок (и его продукт с y) с большей точностью, чем представление с плавающей точкой x а также y, Например, если x а также y являются двойными, и вы хотите получить результат с высокой точностью, вам нужно найти какой-то способ хранения промежуточных результатов (и выполнения арифметики) в формате с более высокой точностью. Формат Intel x87, как и 64-разрядные целые числа, является распространенным выбором (хотя, если вы действительно хотите реализовать высококачественную реализацию, вам потребуется выполнить несколько 96-разрядных целочисленных вычислений, которые в некоторых случаях немного болезненны языки). Намного легче справиться с этим, если вы реализуете powf(float,float)потому что тогда вы можете просто использовать double для промежуточных вычислений. Я бы рекомендовал начать с этого, если вы хотите использовать этот подход.
Алгоритм, который я изложил, не является единственным возможным способом вычисления pow, Это просто самое подходящее средство для получения высокоскоростного результата, который удовлетворяет фиксированной границе априорной точности. Он менее подходит в некоторых других контекстах и, безусловно, гораздо сложнее реализовать, чем алгоритм повторного квадрата [корня], который предложили некоторые другие.
Если вы хотите попробовать алгоритм с повторным квадратом [корень], начните с написания целочисленной функции без знака, которая использует только повторный квадрат. Как только вы хорошо разберетесь в алгоритме для этого уменьшенного случая, вы обнаружите, что достаточно просто расширить его для обработки дробных показателей.
Существуют два разных случая: целочисленные показатели и дробные показатели.
Для целочисленных показателей вы можете использовать возведение в степень путем возведения в квадрат.
def pow(base, exponent):
if exponent == 0:
return 1
elif exponent < 0:
return 1 / pow(base, -exponent)
elif exponent % 2 == 0:
half_pow = pow(base, exponent // 2)
return half_pow * half_pow
else:
return base * pow(base, exponent - 1)
Второй "элиф" - это то, что отличает это от наивной функции Пау. Это позволяет функции совершать O (log n) рекурсивных вызовов вместо O (n).
Для дробных показателей можно использовать тождество a^b = C^(b*log_C(a)). Удобно взять C=2, поэтому a^b = 2^(b * log2(a)). Это сводит проблему к написанию функций для 2 ^ x и log2 (x).
Причина, по которой удобно брать C=2, состоит в том, что числа с плавающей запятой хранятся в базе с плавающей запятой 2. log2 (a * 2 ^ b) = log2 (a) + b. Это облегчает написание вашей функции log2: вам не нужно, чтобы она была точной для каждого положительного числа, только на интервале [1, 2). Точно так же, чтобы вычислить 2^x, вы можете умножить 2 ^ (целая часть x) * 2^(дробная часть x). Первая часть тривиальна для хранения в числе с плавающей запятой, для второй части вам просто нужна функция 2 ^ x на интервале [0, 1).
Трудная часть - найти хорошее приближение 2 ^ x и log2 (x). Простой подход заключается в использовании серии Тейлора.
По определению:
a ^ b = exp (b ln (a))
где exp(x) = 1 + x + x^2/2 + x^3/3! + x^4/4! + x^5/5! + ...
где n! = 1 * 2 * ... * n,
На практике вы можете хранить массив первых 10 значений 1/n!, а затем приблизительный
exp(x) = 1 + x + x^2/2 + x^3/3! + ... + x^10/10!
потому что 10! это огромное количество, так что 1/10! очень маленький (2.7557319224⋅10^-7).
Функции Вольфрама дают широкий спектр формул для вычисления степеней. Некоторые из них будут очень просты в реализации.
Для положительных целочисленных степеней посмотрите на возведение в степень путем возведения в квадрат и возведения в степень сложения.
Использование трех реализованных функций iPow(x, n), Ln(x) а также Exp(x)Я могу вычислить fPow(x, a)х и существо удваивается. Ни одна из функций ниже не использует библиотечные функции, а только итерацию.
Некоторые пояснения о реализованных функциях:
(1) iPow(x, n): х есть doublen это int, Это простая итерация, так как n является целым числом.
(2) Ln(x): Эта функция использует итерацию серии Тейлора. Ряд, используемый в итерации, Σ (from int i = 0 to n) {(1 / (2 * i + 1)) * ((x - 1) / (x + 1)) ^ (2 * n + 1)}, Символ ^ обозначает степенную функцию Pow(x, n) реализовано в 1-й функции, которая использует простую итерацию.
(3) Exp(x)Эта функция снова использует итерацию серии Тейлора. Ряд, используемый в итерации, Σ (from int i = 0 to n) {x^i / i!}, Здесь ^ обозначает степенную функцию, но она не вычисляется путем вызова 1-го Pow(x, n) функция; вместо этого он реализуется в 3-й функции, одновременно с факториалом, используя d *= x / i, Я чувствовал, что должен был использовать этот трюк, потому что в этой функции итерация делает еще несколько шагов относительно других функций и факториала (i!) переполняет большую часть времени. Чтобы убедиться, что итерация не переполняется, степенная функция в этой части повторяется одновременно с факториалом. Таким образом, я преодолел переполнение.
(4) fPow(x, a): x и a оба являются двойными. Эта функция не делает ничего, кроме как просто вызывает другие три функции, реализованные выше. Основная идея этой функции зависит от некоторого исчисления: fPow(x, a) = Exp(a * Ln(x)), И теперь у меня есть все функции iPow, Ln а также Exp с итерацией уже.
нб я использовал constant MAX_DELTA_DOUBLE чтобы решить, на каком шаге остановить итерацию. Я установил это 1.0E-15что кажется разумным для двойников. Итак, итерация останавливается, если (delta < MAX_DELTA_DOUBLE) Если вам нужна дополнительная точность, вы можете использовать long double и уменьшить постоянное значение для MAX_DELTA_DOUBLE, чтобы 1.0E-18 например (1.0E-18 будет минимальным).
Вот код, который работает для меня.
#define MAX_DELTA_DOUBLE 1.0E-15
#define EULERS_NUMBER 2.718281828459045
double MathAbs_Double (double x) {
return ((x >= 0) ? x : -x);
}
int MathAbs_Int (int x) {
return ((x >= 0) ? x : -x);
}
double MathPow_Double_Int(double x, int n) {
double ret;
if ((x == 1.0) || (n == 1)) {
ret = x;
} else if (n < 0) {
ret = 1.0 / MathPow_Double_Int(x, -n);
} else {
ret = 1.0;
while (n--) {
ret *= x;
}
}
return (ret);
}
double MathLn_Double(double x) {
double ret = 0.0, d;
if (x > 0) {
int n = 0;
do {
int a = 2 * n + 1;
d = (1.0 / a) * MathPow_Double_Int((x - 1) / (x + 1), a);
ret += d;
n++;
} while (MathAbs_Double(d) > MAX_DELTA_DOUBLE);
} else {
printf("\nerror: x < 0 in ln(x)\n");
exit(-1);
}
return (ret * 2);
}
double MathExp_Double(double x) {
double ret;
if (x == 1.0) {
ret = EULERS_NUMBER;
} else if (x < 0) {
ret = 1.0 / MathExp_Double(-x);
} else {
int n = 2;
double d;
ret = 1.0 + x;
do {
d = x;
for (int i = 2; i <= n; i++) {
d *= x / i;
}
ret += d;
n++;
} while (d > MAX_DELTA_DOUBLE);
}
return (ret);
}
double MathPow_Double_Double(double x, double a) {
double ret;
if ((x == 1.0) || (a == 1.0)) {
ret = x;
} else if (a < 0) {
ret = 1.0 / MathPow_Double_Double(x, -a);
} else {
ret = MathExp_Double(a * MathLn_Double(x));
}
return (ret);
}
Вы можете найти функцию Pow следующим образом:
static double pows (double p_nombre, double p_puissance)
{
double nombre = p_nombre;
double i=0;
for(i=0; i < (p_puissance-1);i++){
nombre = nombre * p_nombre;
}
return (nombre);
}
Вы можете найти функцию пола следующим образом:
static double floors(double p_nomber)
{
double x = p_nomber;
long partent = (long) x;
if (x<0)
{
return (partent-1);
}
else
{
return (partent);
}
}
С наилучшими пожеланиями
Это интересное упражнение. Вот несколько предложений, которые вы должны попробовать в следующем порядке:
- Используйте петлю.
- Используйте рекурсию (не лучше, но тем не менее, интересно)
- Значительно оптимизируйте рекурсию, используя методы "разделяй и властвуй"
- Используйте логарифмы
Лучший алгоритм для эффективного вычисления положительных целочисленных степеней многократно возводит в квадрат основание, отслеживая при этом дополнительные мультипликаторы остатка. Вот пример решения на Python, которое должно быть относительно простым для понимания и перевода на ваш предпочтительный язык:
def power(base, exponent):
remaining_multiplicand = 1
result = base
while exponent > 1:
remainder = exponent % 2
if remainder > 0:
remaining_multiplicand = remaining_multiplicand * result
exponent = (exponent - remainder) / 2
result = result * result
return result * remaining_multiplicand
Чтобы он обрабатывал отрицательные показатели, все, что вам нужно сделать, это вычислить положительную версию и разделить 1 на результат, так что это должно быть простым изменением приведенного выше кода. Дробные показатели значительно сложнее, поскольку это означает, по существу, вычисление n-го корня основания, где n = 1/abs(exponent % 1) и умножение результата на результат вычисления мощности целочисленной части:
power(base, exponent - (exponent % 1))
Вы можете вычислить корни с желаемым уровнем точности, используя метод Ньютона. Проверьте статью в Википедии об алгоритме.
Я использую арифметику с фиксированной запятой и мой лог основан на log2/exp2. Числа состоят из:
int sig = { -1; +1 }сигнумDWORD a[A+B]числоAэто числоDWORDs для целой части числаBэто числоDWORDс для дробной части
Мое упрощенное решение таково:
//---------------------------------------------------------------------------
longnum exp2 (const longnum &x)
{
int i,j;
longnum c,d;
c.one();
if (x.iszero()) return c;
i=x.bits()-1;
for(d=2,j=_longnum_bits_b;j<=i;j++,d*=d)
if (x.bitget(j))
c*=d;
for(i=0,j=_longnum_bits_b-1;i<_longnum_bits_b;j--,i++)
if (x.bitget(j))
c*=_longnum_log2[i];
if (x.sig<0) {d.one(); c=d/c;}
return c;
}
//---------------------------------------------------------------------------
longnum log2 (const longnum &x)
{
int i,j;
longnum c,d,dd,e,xx;
c.zero(); d.one(); e.zero(); xx=x;
if (xx.iszero()) return c; //**** error: log2(0) = infinity
if (xx.sig<0) return c; //**** error: log2(negative x) ... no result possible
if (d.geq(x,d)==0) {xx=d/xx; xx.sig=-1;}
i=xx.bits()-1;
e.bitset(i); i-=_longnum_bits_b;
for (;i>0;i--,e>>=1) // integer part
{
dd=d*e;
j=dd.geq(dd,xx);
if (j==1) continue; // dd> xx
c+=i; d=dd;
if (j==2) break; // dd==xx
}
for (i=0;i<_longnum_bits_b;i++) // fractional part
{
dd=d*_longnum_log2[i];
j=dd.geq(dd,xx);
if (j==1) continue; // dd> xx
c.bitset(_longnum_bits_b-i-1); d=dd;
if (j==2) break; // dd==xx
}
c.sig=xx.sig;
c.iszero();
return c;
}
//---------------------------------------------------------------------------
longnum pow (const longnum &x,const longnum &y)
{
//x^y = exp2(y*log2(x))
int ssig=+1; longnum c; c=x;
if (y.iszero()) {c.one(); return c;} // ?^0=1
if (c.iszero()) return c; // 0^?=0
if (c.sig<0)
{
c.overflow(); c.sig=+1;
if (y.isreal()) {c.zero(); return c;} //**** error: negative x ^ noninteger y
if (y.bitget(_longnum_bits_b)) ssig=-1;
}
c=exp2(log2(c)*y); c.sig=ssig; c.iszero();
return c;
}
//---------------------------------------------------------------------------
где:
_longnum_bits_a = A*32
_longnum_bits_b = B*32
_longnum_log2[i] = 2 ^ (1/(2^i)) ... precomputed sqrt table
_longnum_log2[0]=sqrt(2)
_longnum_log2[1]=sqrt[tab[0])
_longnum_log2[i]=sqrt(tab[i-1])
longnum::zero() sets *this=0
longnum::one() sets *this=+1
bool longnum::iszero() returns (*this==0)
bool longnum::isnonzero() returns (*this!=0)
bool longnum::isreal() returns (true if fractional part !=0)
bool longnum::isinteger() returns (true if fractional part ==0)
int longnum::bits() return num of used bits in number counted from LSB
longnum::bitget()/bitset()/bitres()/bitxor() are bit access
longnum.overflow() rounds number if there was a overflow X.FFFFFFFFFF...FFFFFFFFF??h -> (X+1).0000000000000...000000000h
int longnum::geq(x,y) is comparition |x|,|y| returns 0,1,2 for (<,>,==)
Все, что вам нужно, чтобы понять этот код, это то, что числа в двоичной форме состоят из суммы степеней 2, когда вам нужно вычислить 2^num, тогда это можно переписать так:
2^(b(-n)*2^(-n) + ... + b(+m)*2^(+m))
где n дробные биты и m являются целочисленными битами. умножение / деление на 2 в двоичном виде просто сдвиг битов, так что если вы сложите все вместе, вы получите код для exp2 похоже на мое. log2 основан на бинарном поиске... изменение битов результата с MSB на LSB до совпадения с искомым значением (очень похожий алгоритм для быстрого вычисления sqrt). надеюсь, это поможет прояснить ситуацию...
Много подходов дано в других ответах. Вот кое-что, что я думал, может быть полезным в случае интегральных полномочий.
В случае целочисленной степени x от n x, простой подход потребовал бы умножения x-1. Чтобы оптимизировать это, мы можем использовать динамическое программирование и повторно использовать более ранний результат умножения, чтобы избежать всех х умножений. Например, в 5 9 мы можем, скажем, сделать пакеты из 3, то есть вычислить 5 3 один раз, получить 125, а затем куб 125, используя ту же логику, принимая в процессе только 4 умножения вместо 8 умножений простым способом.,
Вопрос в том, каков идеальный размер партии b, чтобы количество умножений было минимальным. Итак, давайте напишем уравнение для этого. Если f(x,b) является функцией, представляющей количество умножений, использованных при вычислении n x с использованием вышеупомянутого метода, то
Пояснение: Произведение из серии чисел p будет умножаться на p-1. Если мы поделим x умножений на b пакетов, в каждом пакете потребуется (x/b)-1 умножений, а для всех b пакетов потребуется умножение b-1.
Теперь мы можем вычислить первую производную этой функции по b и приравнять ее к 0, чтобы получить b для наименьшего числа умножений.
Теперь верните это значение b в функцию f(x,b), чтобы получить наименьшее количество умножений:
Для всех положительных x это значение меньше, чем умножения прямым способом.
Возможно , вы можете использовать расширение ряда Тейлора. Ряд Тейлора функции представляет собой бесконечную сумму членов, которые выражаются через производные функции в одной точке. Для наиболее распространенных функций функция и сумма ее ряда Тейлора вблизи этой точки равны. Серии Тейлора названы в честь Брука Тейлора, который представил их в 1715 году.
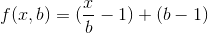
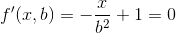 2 + 1 = 0">
2 + 1 = 0">