Нарисуйте многогранник с метрическими размерами над частью сферы, используя d3-geo

Question

У меня есть следующие потребности:

учитывая многоугольник с метрическими размерами, мне нужно нарисовать его над определенной частью сферы, а затем вывести его в формате GeoJSON.

Кроме того, "часть сферы" представляет собой прямоугольник, состоящий из 4 точек, которые можно вращать относительно линии экватора.

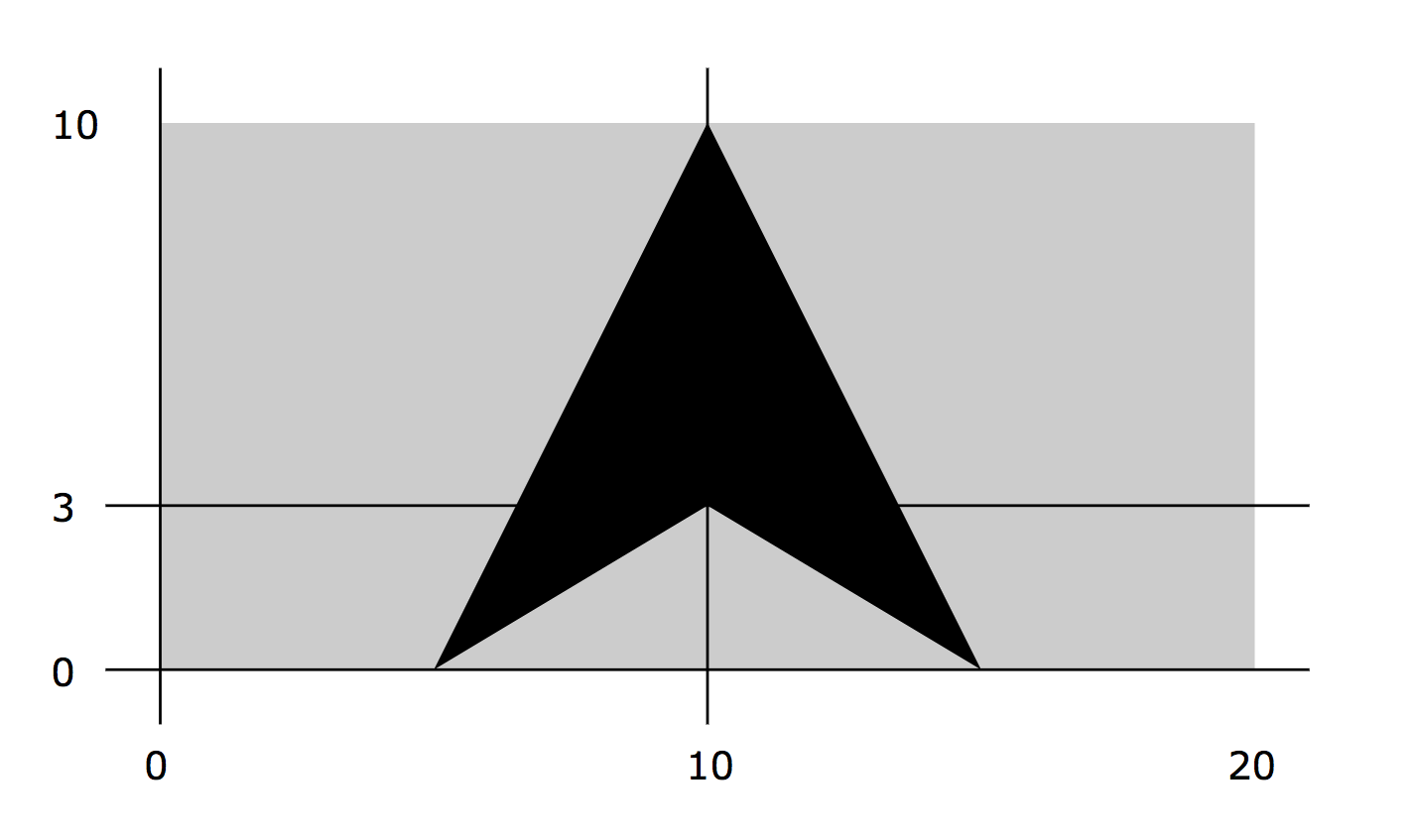
в качестве примера представим MultiPolygon с прямоугольником в нем, например, где числа в метрах:

[
  [
    [
      [0, 10],
      [0, 0],
      [20, 0],
      [20, 10]
    ]
  ]
]

как видите, такой многоугольник выровнен под прямым углом к ​​оси.

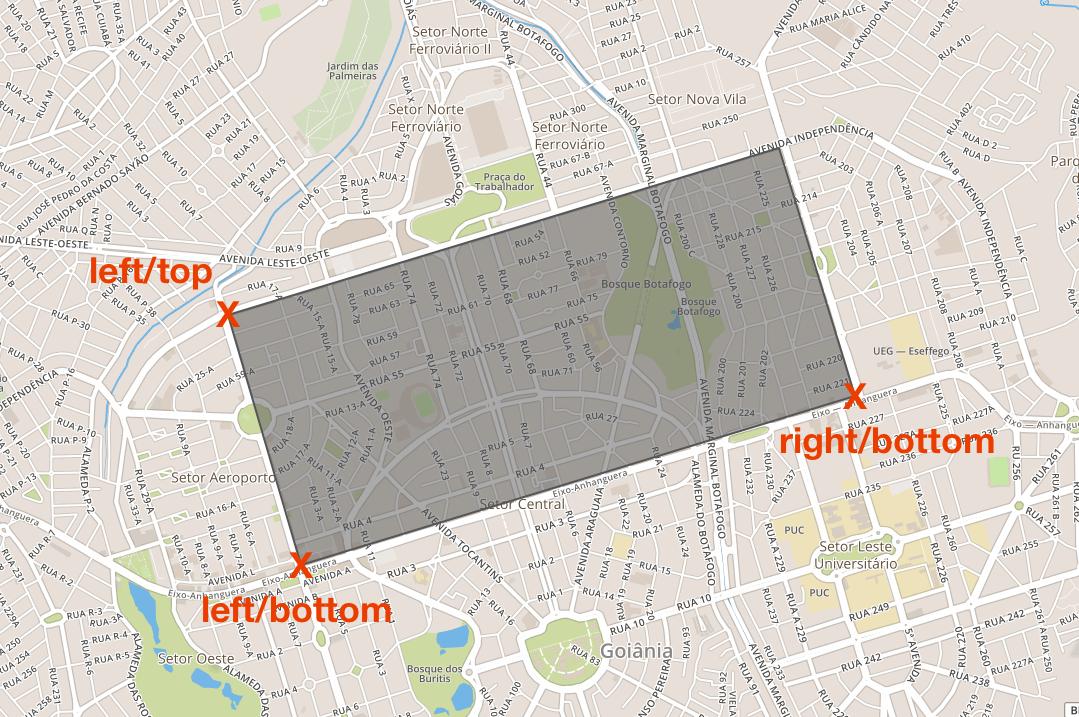
Затем, учитывая любую прямоугольную область сферы, например, приведенную ниже:

{
    leftTop: [ 13.377948, 52.521293 ],
    leftBottom: [ 13.377962, 52.521250 ],
    rightBottom: [ 13.378174, 52.521275 ],
    rightTop: [ 13.378161, 52.521318 ]
}

Я хочу перевести, повернуть и подогнать этот многоугольник в этой области.

Итак, пакет d3-geo предлагает подходящие инструменты, такие как projection с комбинацией масштаба / переводить / вращать / приспосабливать с инвертированием и так далее. Но я не могу найти правильную комбинацию для работы с повернутыми прямоугольными областями.

Поскольку подавляющее большинство примеров d3-geo в Интернете относятся либо к GeoJSON к пикселям, либо к использованию d3 в качестве движка рендеринга SVG, и т. Д., Мне трудно абстрагировать свои потребности в вызовах функций.

У кого-нибудь есть свет, чтобы помочь мне решить это? Я предполагаю, что в Геометрии / Тригонометрии должен быть правильный термин для описания такого расчета.

Я использовал для себя "проецирование плоского многоугольника на геодезическую область", но я думаю, что должен быть лучший и более конкретный термин. По крайней мере, если я найду такой термин, это будет хорошим началом.

Обновить:

Я составил несколько иллюстраций того, чего я пытаюсь достичь. Имейте в виду, что, хотя они здесь и являются визуальными изображениями, в моем случае я не ищу инструменты визуального рендеринга, поскольку сделаю просто преобразование из Array / Objects в GeoJSON.

1. Многоугольник, который я хочу проецировать. Обратите внимание, что на светло-сером поле отображается виртуальная область, в которой расположен такой многоугольник, поэтому, поскольку многоугольник находится в середине, его также необходимо спроецировать на середину географической области.

2. Прямоугольный сектор над геоидом (Земля в данном случае). Обратите внимание на красные метки, указывающие контрольные углы, которые должны указывать вращение.

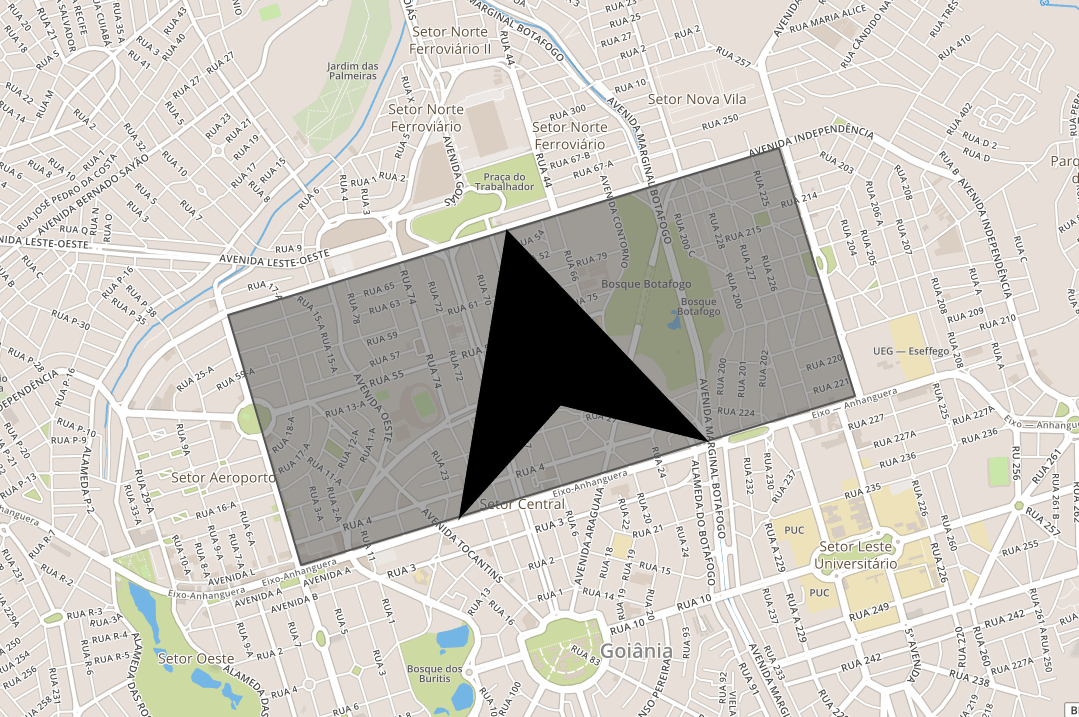
3. Результат с многоугольником, спроецированным в заданную область (который будет фактически в формате GeoJSON, с соответствующими координатами).

Answer 1

Если я правильно понимаю проблему, я считаю, что у меня есть решение. Тем не менее, вопрос довольно широкий без какого-либо кода, следовательно, мой ответ будет довольно широким, но должен четко обозначить подход для достижения желаемого результата.

Основываясь на изображениях, проблема выглядит следующим образом: Как вписать фигуры в географические ограничивающие рамки, где ограничивающие рамки проецируются в плоское пространство и могут иметь поворот.

Если это верно, то мой ответ должен быть полезен. Для ясности, когда я использую слово "форма", я ссылаюсь на негеографический многоугольник.

Общая схема решения:

1. Получить ориентацию исходного полигона
2. Поверните карту, а не форму
3. Используя geoIdentity, поместите форму в географическую ограничивающую рамку

4. а. Закончите, применяя противоположное вращение, как вы начали,

   б. Поверните весь svg/canvas, чтобы противостоять начальному вращению; или же,

   с. Держите повернутую карту.

---

Получение ориентации географического прямоугольника

Вам необходимо установить поворот географического объекта относительно плоскости проекции, это, по-видимому, суть проблемы (Вы указываете повернутую прямоугольную область сферы, но области могут быть только прямоугольными в проецируемом пространстве и основаны на изображения, эта интерпретация представляется правильной).

D3 может быть немного сложным в этом отношении, так как он не отображает пути вдоль декартовых координат, но интерполирует большие расстояния окружности. Это будет в большей степени проблемой для географических объектов размером страны или континента, но должно быть незначительным в масштабе города.

Если начать с верхней левой точки ([x1,y1 ]) и используя нижнюю правую точку ([x2,x1]), вы должны быть в состоянии определить угол этой линии относительно того, каким он должен быть: вертикальная линия, начинающаяся с первой координаты и заканчивающаяся второй. Учитывая, что порядок намотки имеет значение с d3, если у вас есть одна точка, вторая координата всегда будет соответствовать одной и той же вершине прямоугольника.

Метод получения этого угла довольно прост:

var p1 = [long,lat];   // geographic coordinate space for the two points
var p2 = [long,lat];

var x1 = projection(p1)[0];  // projected svg coordinate space for the two points
var x2 = projection(p2)[0];
var y1 = projection(p1)[1];
var y2 = projection(p2)[1];

var dx = x1 - x2;  // run
var dy = y1 - y2;  // rise

var angle = Math.atan(dx/dy);  // in radians, multiply by 180/π to get degrees

Мы проецируем две координаты, вычисляя спроецированные различия в координатах x и y, измеренные в пикселях. Запустите его через Math.atan(), и у нас будет угол.

Но подождите, это еще не все.

Поворот карты

Метод, который мы использовали для вычисления угла, хорош, но нам нужно изменить его, чтобы повернуть карту. Если мы повернем карту, она будет вращаться вокруг [0,0] (long,lat), центр вращения по умолчанию для большинства проекций. Нам нужно центрировать карту на [-x,-y] где x и y представляют среднюю точку двух точек, используемых для вычисления ориентации, измеренной в пространстве географических координат (не спроецировано).

Нам нужно центрировать карту по вращению, прежде чем вычислять угол, так как это изменит угол. Для этого нам нужен d3.geoInterpolate, который вычисляет точки от p1 (0) до p2 (1), нам нужна половина пути, поэтому мы кормим ее 0,5:

var pMid = d3.geoInterpolate(p1, p2)(0.5);

Теперь мы можем применить его к проекции до вычисления угла:

projection.rotate([-pMid[0],-pMid[1]]);

Почему отрицательные значения? Мы двигаем землю под себя

Теперь мы можем пройти расчет угла. Когда у нас есть угол, мы можем применить его:

projection.rotate([-pMid[0],-pMid[1],-angle])  // angle in degrees

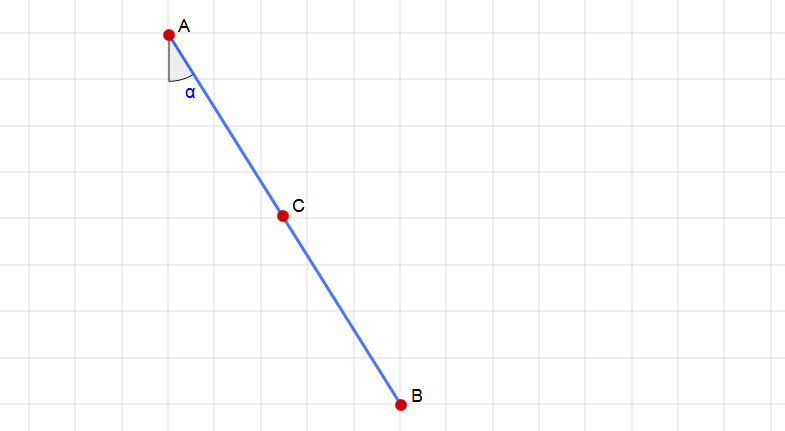
Мы на полпути, используя изображение ниже, мы использовали географические координаты A и B, чтобы определить географический центр C. Затем, используя проекционные координаты A и B, мы определяем угол α, который затем используем для поворота проецируемого координаты, так что линия AB является вертикальной на карте.

Подогнать фигуру к географической ограничивающей рамке

Таким образом, мы решили половину проблемы, теперь нам нужно спроецировать форму. Мы будем использовать вторую проекцию для фигуры, сработает простая геоидентификация, она позволяет нам использовать метод fitSize или fitExtent при проецировании координат без преобразования. Просто обратите внимание, что вы, вероятно, хотите перевернуть эту функцию по оси y: значения svg y начинаются с 0 сверху, более стандартные декартовы значения y начинаются снизу.

Мы хотим использовать fitExtent, который позволит нам установить ограничивающий прямоугольник для фигуры. proejction.fitExtent([[x,y],[x,y]],feature) берет массив, содержащий верхний левый и нижний правый углы ограничивающего прямоугольника (в координатах svg) для хранения объекта (объект геоджон).

Имейте в виду, что спроецированный нами географический объект будет более прямоугольным, чем меньше его географический (не спроецированный) размер, тем более крупные области могут иметь меньше квадратных свойств, особенно по отношению к правой стороне прямоугольника. Для больших географических областей вам может потребоваться пересмотреть расчет вращения, но в какой-то момент спроецированные прямоугольники просто не совпадают с "прямоугольниками" на сфере.

Чтобы получить ограничивающий прямоугольник для fitExtent, мы можем использовать path.bounds():

Возвращает спроецированную плоскую ограничивающую рамку (обычно в пикселях) для указанного объекта GeoJSON. Ограничительная рамка представлена ​​двумерным массивом: [[x₀, y₀], [x₁, y₁]], где x₀ - минимальная x-координата, y₀ - минимальная y-координата, x₁ - максимальная x-координата, и y₁ - максимальная y-координата. ( API документы)

Отлично, теперь у нас есть две ограничивающие рамки, которые должны иметь одинаковые точки, мы используем:

projection2.fitExtent(path.bounds(geoRectangle));

Теперь мы наложили форму на географический объект:

var feature = { "type": "Feature","properties": {},"geometry": {"type": "Polygon","coordinates": [ [ [-81.62841796875,24.307053283225915],[-75.9375,21.88188980762927],[ -77.3876953125,18.8543103618898],[       -83.1884765625,21.268899719967695 ], [-81.62841796875,24.307053283225915]]]}};
var triangle = {"type": "Polygon","coordinates": [[[0, 0], [10, 10], [20, 0], [0, 0]]]};


var width = 500; var height = 300;
var svg = d3.select("body")
  .append("svg")
  .attr("width",width)
  .attr("height",height);
  
var projection = d3.geoMercator().scale(500/Math.PI/2).translate([width/2,height/2]);
var path = d3.geoPath().projection(projection);


d3.json("https://unpkg.com/world-atlas@1/world/110m.json", function(error, world) {
  if (error) throw error;

  var p1 = feature.geometry.coordinates[0][1]; // first point in geojson
  var p2 = feature.geometry.coordinates[0][2]; // second point in geojson
  
  var pMid = d3.geoInterpolate(p1, p2)(0.5);   // halfway point between both points
  
  projection.rotate([-pMid[0],-pMid[1]]);                          // rotate the projection to center on the mid point
  projection.fitExtent([[135,135],[width-135,height-135]],feature) // optional: scale the projected feature, may offer benefits for very small features
 
  var dx = projection(p1)[0] - projection(p2)[0]; // run, difference between projected points x values
  var dy = projection(p1)[1] - projection(p2)[1]; // rise, difference between projected points y values
  
  var a = Math.atan(dx/dy) * 180 / Math.PI; // get angle and convert to degrees
  
   projection.rotate([-pMid[0],-pMid[1],-a]);  // adjust rotation to straighten feature
   projection.fitExtent([[135,135],[width-135,height-135]],feature) // scale and translate the feature.
   
  // draw world map, draw feature
  svg.append("path")
    .attr("d",path(topojson.mesh(world)))
    .attr("fill","none")
    .attr("stroke","black")
  
  svg.append("path")
    .attr("d", path(feature))
    .attr("fill","none")
    .attr("stroke","steelblue");


  // set up the projection and path for the shape       
  var projection2 = d3.geoIdentity().reflectY(true);
  var path2 = d3.geoPath().projection(projection2);

  // scale the shape's projection for the shape using the bounds of the geographic feature
  projection2.fitExtent(path.bounds(feature),triangle);

  // draw the shape
  svg.append("path")
    .attr("d", path2(triangle));
  
});

<script src="https://cdnjs.cloudflare.com/ajax/libs/d3/4.11.0/d3.min.js"></script>
<script src="https://unpkg.com/topojson-client@3"></script>

Это нарисованный от руки многоугольник, я поместил визитную карточку на монитор и проследил ее, следовательно, недостатки больше, чем обычно

Конец игры

Теперь у вас есть фигура, нарисованная и наложенная поверх некоторой географической особенности, надеюсь, довольно прилично. Что теперь? Технически это решает ключевую проблему, но мы создали новую, если вам не нужна наклонная карта. Варианты решения этой проблемы - вращение всего svg/canvas или взятие каждой точки в форме и перепроектирование их и превращение их в географические координаты, а не скучные старые декартовы. Есть и другие, но эти два кажутся наиболее простыми.

Если вы работаете с изображениями, вы можете перепроектировать изображение попиксельно, но не ожидайте, что это будет быстрым, посмотрите этот блок. Этот ответ рассматривает изображения и подгоняет их к проекции, если они имеют известные границы, при очень малых расстояниях Меркатор должен нормально работать как проекция.

Перепроектирование точек и геоидентичности

Как указано в комментариях, d3.geoIdentity делает перепроектирование невозможным, если следовать шаблону: var latlong = projection.invert(projection2([x,y])), поскольку geoIdentity не возвращает функцию, просто объект. Вместо этого мы можем определить поведение (переключение на y и использование масштабирования и преобразования идентичности):

projection2.project = function([x,y]) {
  var s = this.scale();
  var t = this.translate();
  return [(x * s) + t[0] , -y * s + t[1]]
}

Который в поверхностном тестировании возвращает проецируемую точку, которая является стандартным поведением геопроекции, не включенной в геоидентификацию. Шаблон использования должен выглядеть так:

projection.invert(projection2.project([x,y]))

Answer 2

Я нашел способ реализовать то, что мне нужно, хотя я не использовал d3-geo, но вместо этого использовал комбинацию Turf.js и геодезических библиотек.

Вот оно (поиск по запросу "projectPlainOverGeoArea"):

https://gist.github.com/marinho/8a7e71b53c7da97f9579146742bb54de

Код делает следующее:

1. рассчитать ширину и высоту в метрах расстояния от географического прямоугольника (область, которую я хочу проецировать). Используются сферические /haversine функции геодезии

2. спроецируйте каждую точку каждого пути многоугольника на эквивалентные географические координаты, используя пропорциональные расстояния от прямоугольника многоугольника до географического прямоугольника. Результатом здесь является многоугольник ожидаемых мер, выровненный по линии экватора.

3. использует TransformRotate Turf, чтобы вращать проецируемый многоугольник, используя левое / нижнее в качестве оси вращения

Кажется, это хорошо работает в тестах, которые я сделал, но, честно говоря, я недоволен этим, так как считаю, что должно быть более элегантное решение для него с d3-geo или другой библиотекой.